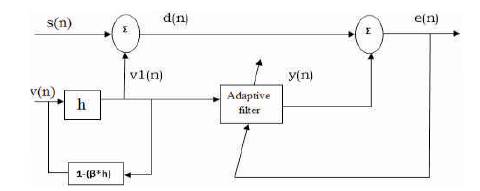
Figure 1. Block Diagram of Shadow-based Fixed LMS Adaptive Filter
This paper explains the implementation based on adaptive filter algorithm with shadow technique, which belongs to the class of LMS algorithm on FPGA. The objective of this paper is to cancel out additive noise due to the effect of environmental conditions in the communication system. The additive noise is one of the major problems in the communication, especially in the digital electronic circuits design these days. Generally, the coefficient of filter updation is not in a basic filter time to time, as it may be an effect on the desired information. By updating coefficient of filter time to time, this problem could be eradicated and by increasing the number of iterations for the filtering process, it would give an efficient result. The popular method used to cancel out the additive noise in the communication systems is the Least Mean Square (LMS) algorithm. Here, a novel shadow based technique is employed in fixed LMS adaptive filter for improving the spectral characteristics like Side Lobe Attenuation (SLA), Main Lobe Width (MLW), Side Lobe Fall of Ratio (SLFR) of the filter by changing the feedback factor 'β'. In this project, it is found that the performance of shadow based fixed LMS is improved when compared to the existed fixed LMS in terms of signal-to-noise ratio (SNR) and Mean Squared Error (MSE) done with the help of MATLAB tool, and this proposed project was implemented on FPGA with utilization of minimum number of logic gates, flip flops, LUT's, and registers that are operated at maximum frequencies. This paper also compares the number of flip flops, logic gates, LUT's, and registers utilized for different resources in the family of FPGA. In real time applications, the adaptive filter algorithm implementation on FPGA plays a crucial role, especially in the DSP processors for effective communication. By introducing the concept of shadow technique in the adaptive filtering, the additive noise would be suppressed in the communication systems. The core FPGA is designed such that, it can be implemented in any brand of SoPC. In this paper, SPARTAN 3E and Vertex 4 are the application platform of FPGA. The achieved results gives an improvement in area resource utilization, convergence rate, speed, and performance in design pure LMS hardware core. Implementing the LMS adaptive filter algorithm on FPGA is achieved in VERILOG hardware description languages.
Adaptive filters, as part of digital signal systems, have been widely used in communication systems, and also in applications such as adaptive noise cancellation, adaptive beam forming, and channel equalization [1]. However, its implementation takes a great deal and becomes a very important field in digital system design. An adaptive filter is usually implemented in DSP processors because of their capability of performing floating-point arithmetic. Now-a-days, DSP processors play a vital role, as they are portable and compatible with the other family of microprocessors. Especially in the VLSI technology, scale down is one of the important factors, the adaptive filter structure satisfies and also in various fields. It is possible get the effective solutions for adaptive filtering process in Application Specific Integrated Chips (ASIC), General Purpose Processor (GPP), and Digital Signal Processor (DSP). Although, ASIC chips could provide a solution to meet hard constraints, it lacks the flexibility, i.e. available in the other areas also. But when FPGA (Field Programmable Logic Array) grows in an area, which provides many facilities to the designers and has become the competitor in the signal processing market [2, 6, 7]. In addition, FPGA is a form of programmable logic, which offers flexibility for repetitive reconfiguration. Since FPGA consists of slices arranged as array of rows and columns, a very great degree of parallelism can be explored. Although it is not efficient to use floating-point arithmetic in FPGA due to its need for a large area, it is sufficient to use fixed-point arithmetic for the adaptive filter to work well [4]. In general, the FIR filter structure has been used more successfully than the IIR filter structure in adaptive filters. However, when the adaptive FIR filter was made, this required an appropriate algorithm to update the filter's coefficients [3, 5]. The output FIR filters is the convolution of its input with its coefficients which have constant values [8- 10]. The Least Mean Square (LMS) algorithm is an algorithm used to update the filter coefficient which is known for its simplification, low computational complexity, and better performance in different running environments [11]. The obtained results show improvements in area-resource utilization, convergence speed and performance in the designed pure-hardware LMS core [12]. Although using a pure-hardware implementation results in high performance, it is much more complex than other structures [15].
Least mean square filtering mechanism is the one of the familiar mechanism in the speech signal processing. The Least Mean Square (LMS) algorithm is a powerful algorithm was developed by Windrow and Hoff in 1960. In this method, the current output of the filter does not depend on the previous output. The general structure of LMS adaptive filter is as shown in Figure 1.

Figure 1. Block Diagram of Shadow-based Fixed LMS Adaptive Filter
Figure 1 shows the block diagram of Adaptive filter with Fixed LMS Algorithm with Shadow concept [13-14]. In shadow filter mechanism, the Low pass filter output is feedback either positively or negatively by a shadow filter of same type or different type. Here, the shadow mechanism is used to improve spectral characteristics of FIR filter with best combination for different values of 'β'. The derived expression of the transfer function for the shadow mechanism with positive feedback connection is,
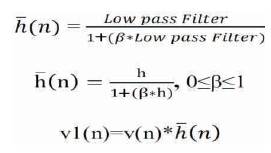
The process of selecting the beta (β) parameters so as to achieve the better match between the desire signal and the filter output is often done by optimizing an appropriately defined Performance function. As in Figure 1, the Shadow based LMS Adaptive Filter is a dual-input with close-loop adaptive feedback system, one is the primary input signal d(n), which is the desire signal added by the noise, and another is the reference signal v1(n) which is the noise sample.
According to this technique, the Adaptive filter gives an error signal as an output which is the difference between the desired signal and the filter output signal (estimated noise). Then this error signal used as a feedback is given to the adaptive filter to adjust their filter coefficient to obtain the desired filter output. Therefore, in this paper implementing such technique with shadow based concept would be successfully applied to enhance the speech for many applications such as channel equalization, desired EEG signal for detecting brain tumor, speech enhancement, etc.
The updated filter weight formula is given below.
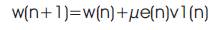
Where,
w(n)=current weight of the filter
μ = step size parameter
s(n)= input speech signal
v1(n)=reference noise signal
y(n)= w*v1(n)= estimated noise
e(n)=d(n)-y(n)= reproduced speech signal at the receiver.
The performance of the adaptive filter is also analyzed by the rate of convergence. In the communication systems, the rate of convergence is as small as possible for excellent speech signal processing. The limitation for the rate of convergence belongs to the family of LMS adaptive filters given as,
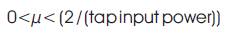
The architecture of shadow based LMS adaptive filter is shown in Figure 2. Here the proposed mechanism is used with the best combination for different values of 'β'. The inputs of shadow mechanism are filtering coefficient (h), beta and Noise to generate defined noise (h3). The noise generated through shadow based FIR filter is added to the source signal to generate corrupt speech (d). The adaptive filter generates the filter output (y) based on the update weight (w) and the defined noise (h3). The noise canceller generates the error (e) by subtracting the adaptive filter output from corrupted speech signal, which is also generates the acknowledgement (Ack_out) for valid output. The filter coefficient of adaptive filter is updated based on the Least Means Square (LMS) algorithm. The inputs of weight update block is step size (mu), present weight value (w), and error (e) to generate weight update value (w1), and also generates Acknowledgement of iteration completed (Ack_ite). The architecture view of adaptive noise canceller with two inputs source and noise with a feedback factor beta (β) is as shown in the architecture.
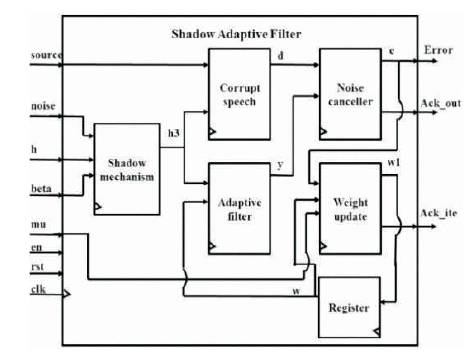
Figure 2. Architecture of Shadow based LMS Adaptive Filter
Although behavior analysis of the LMS algorithm is important to mention that the step-size parameter plays a significant role in the convergence characteristics of the algorithm and also in its stability condition. In order to achieve the better stability, it must satisfy 0 < μ < 2/λmax in the point of view of the rate of convergence fixed LMS gives slower rate of convergence.
Figure 3 shows the flowchart for the processing of initializing the weights w(n) and input coefficients x(n) to obtain the filter output and compute estimated error e(n). The simulation results using matlab tool are discussed below:
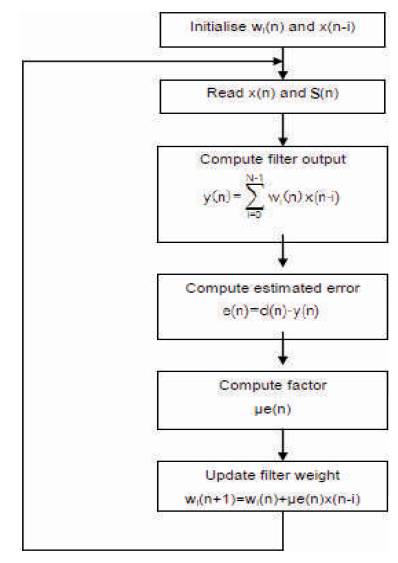
Figure 3. Flowchart for Weight Updation Process in Shadowbased Fixed LMS Adaptive Filter Algorithm
In the first simulation, a speech signal which is distorted with a noise signal is applied to the shadow adaptive filter with a beta factor of 0.1 and the denoised speech is obtained as shown in Figure 4 and Table 1.
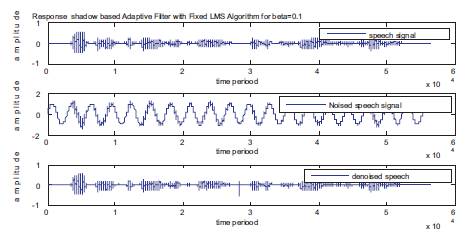
Figure 4. Simulation Result for the Proposed Fixed LMS Adaptive Algorithm with a Feedback Factor of 0.1

Table 1. Result of Figure 4
In the second simulation, a speech signal which is degraded with noise signal is applied to the shadow adaptive filter with a beta factor of 0.5 and the denoised speech is obtained as shown Figure 5 and Table 2.
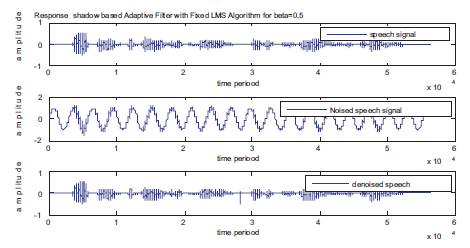
Figure 5. Simulation Result for the Proposed Fixed LMS Adaptive Filter with a Feedback Factor of 0.5

Table 2. Result of Figure 5
In the third simulation, a speech signal which is deformed with noise signal is applied to the shadow adaptive filter with a beta factor of 1.0 and the denoised speech is obtained as shown Figure 6 and Table 3.
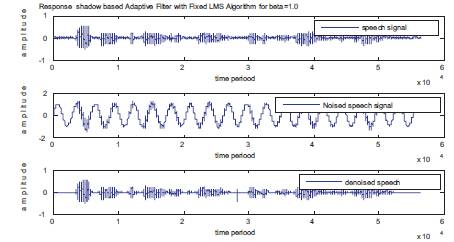
Figure 6. Simulation Result for the Proposed Fixed LMS Adaptive Algorithm with a Feedback Factor of 1.0.

Table 3. Result of Figure 6
Basically, Xilinx is a synthesis and a simulation tool for designing the complex integrated circuits. The performance of these complex integrated circuits can be analyzed by inputs which are in the form of bits or bytes or decimal or hexadecimal numbers in other terms it can be analyzed in the form of digits. This paper analyzed the performance of the adaptive filter having inputs of width 8. The adaptive filter consists of an input source, and a noise of size 8. In order to analyze the timing verification process, it uses a single clock signal. Also to introduce the concept of shadow technique, it uses shadow factor beta of size 8. For activating all the elements in the circuit, it uses enable, and reset inputs named as en, and rst. In this paper, the adaptive filter core is designed in a hardware description language called Verilog and is simulated in Xilinx_ ISE design suite 14.4.
The entity of circuit which is designed in VHDL/Verilog hardware description language is simply a black box shown in Figure 7 which contains only the input ports and output ports.
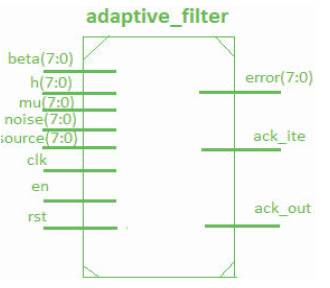
Figure 7. Entity View of Shadow-based LMS Adaptive Filter
Figure 8 illustrates the adaptive filter implementation in the point of view of Register Transfer Logic. In this logic system every digital circuitry consists of Registers that stores the single bit of data or multi stream of data bits. The connections between internal circuitry of the system is simply called as nodes (or) signals.
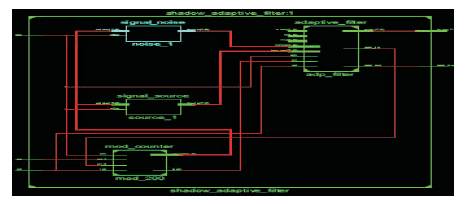
Figure 8. RTL Schematic View of Shadow-based LMS Adaptive Filter
Xilinx ISE design software offers different family of devices to design different complex integrated digital circuits like SPARTAN 3E, Vertex 4, 5…….and different number of series of families are also available. The top view of SPARTAN 3E is as shown in Figure 9.

Figure 9. Top view of SPARTAN-3E Kit
The simulation results obtain by the shadow adaptive filter Core is discussed below.
Figure 10 interprets the timing verification of the system and also provides functional working of the project. At a particular instant of the clock pulse, it produce the result. It verifies the suppression of noise content, in other terms the value of the reproduced signal bits (or) de-noised bits (error(7:0)) bits is nearly equal to the values of the input source signal (7:0). It is thus, observed that the unwanted noise signal are added as an additive noise in the communication system is suppressed.
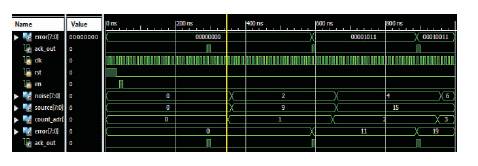
Figure 10. Simulation Results of Shadow-based LMS Adaptive Filter
The implemented proposed LMS core on Xilinx SPARTAN_3e FPGA, Vertex 5v shows that the maximum operating frequency of the shadow based LMS adaptive filter algorithm is 99.93 MHz,and 208.75MHz, respectively.
From the chipScope analyzer, it is observed that the realization of shadow based adaptive filter with the inputs of speech (s), Noise (n) and error (e ≈s) with a particular memory location is shown in Figure 11.
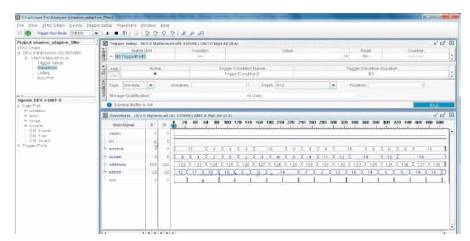
Figure 11. ChipScope Analyzer Output
Table 4 shows the source(s) and noise(n) values and the obtained de-noised speech, i.e. error (e) values (s≈e) with a particular memory location.
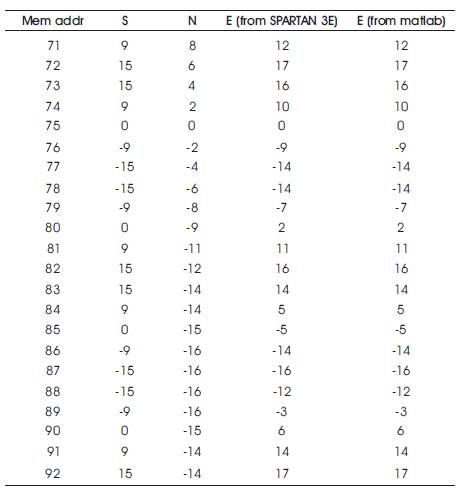
Table 4. Validation Table of Shadow-based LMS Adaptive Filter
The Shadow based LMS Adaptive Filter was implemented by using 8 bit 2's complementation representation for samples and weight values. Here for implementing the Shadow based LMS Adaptive Filter, it is concentrated on Adaptive filter core which uses the target different FPGA devices and design under the plan of Xilinx 14.4.
Resource utilization of proposed adaptive filter algorithm is implemented on FPGA Spartran 3E with devices ft256, fg320, ff668, and ff665 are tabulated in Tables 5 to 8 respectively.
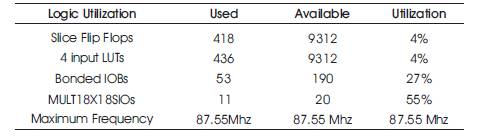
Table 5. Implementation Resource Utilization on xc3s500e-4-ft256
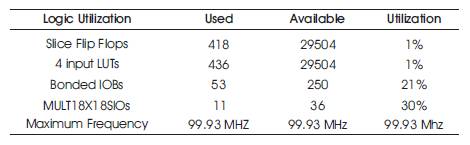
Table 6. Implementation Resource Utilization on xc3s1600e-5-fg320
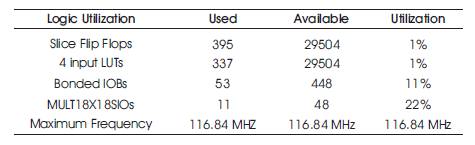
Table 7. Implementation Resource Utilization on xc4vlx25-12-ff668
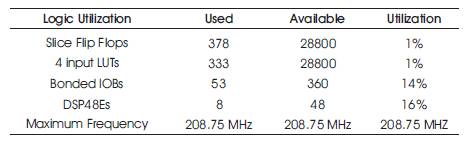
Table 8. Implementation Resource Utilization on xc5vlx50t-3-ff665
Shadow Adaptive Filter is a technique to remove the unwanted additive noise from the obtained signal with the help of the proposed Adaptive filter, which can be applied whenever a suitable reference signal is available. In this paper, the shadow Adaptive filter uses LMS algorithm for updating the filter coefficient as it is found to be the most efficient training algorithm for FPGA based adaptive filter. Therefore, it represents the strategies and hardware implementation of the shadow based LMS adaptive filter Core using Verilog HDL and is simulated using Xilinx ISE 14.4. In case of high speed requirement, Vertex-5 board is used, since it gives the maximum frequency than other FPGA boards. An active noise cancellation system was successfully simulated and implemented. The system met all requirements and the ultra-sound data was properly filtered, and the audio data was adequately filtered to recover the target signal. These requirements were accomplished in both simulation and hardware. In the future, this work may be implemented on DSP processor to get better results. Also, the hardware can be designed into a real-time platform using microphones and speakers to detect the audio signals and perform the filtering on them. The speakers could then be used to generate a sound wave to negate the noise. This approach would require extensive study into acoustics too.