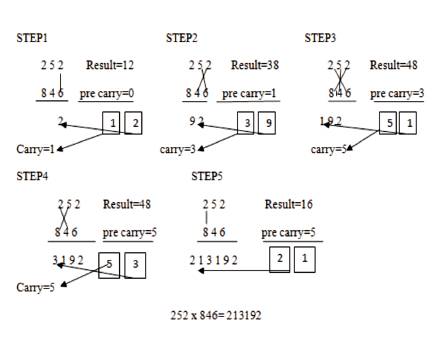
Figure 1. Multiplication of Two Decimal Numbers: 252x846
This paper is devoted to design a high-speed Arithmetic Logic Unit. All of us know that, ALU is a module which can perform arithmetic and logic operations. The speed of ALU greatly depends upon the speed of the Multiplier. This paper presents a technique called, “Vedic Mathematics” for designing the multiplier that is fast as compared to other multipliers based on mathematical techniques that have been in practice for a long time. Here, a high-speed 32x32 bit multiplier is designed and analyzed which is based on the Vedic mathematics mechanism. The proposed method is efficient and fast, wherein the processing involves the vertical and crossed multiplication of precedent Vedic mathematics. The internal multiplier is implemented using Vedic-Wallace structure for high-speed implementation. The exponent of the final result is obtained by using Brent-Kung adder for fast computations with less area utilization. The projected Vedic multiplier is coded in a High-level Digital Language (VHDL) followed by synthesization using an EDA tool, XilinxISE14.5. The proposed ALU is able to perform three different arithmetic and eight different logical operations at high speed. The main objective of this paper is to increase the speed of the multiplier and to decrease the delay, and area of the hardware.
With the passage of time, the multipliers have been proven as an essential component, while designing microprocessors and other applications where the processing of a signal is in the foreground. With the advent and improvements in VLSI technology that has enabled the integration of transistors based on different technologies like CMOS, BICMOS technologies, etc., the speed of computation has been increased dramatically. To obtain the performance, parallel processing and pipelining techniques are used to perform the various operations. High-speed processors and hence we require high- speed multipliers [1]. Since a processor depends on its multiplier, multiplication is the key arithmetic procedure for the improvement of fast processor. A reduction in time delay along with power consumption is the important requirement. The word “VEDIC” is a consequential of “VEDA” comprising an accumulation of knowledge at a single platform [15]. Further more, it exhibits 16 sutras that deal with several subdivisions including arithmetic, algebra, geometry and so on [3]. Jagadguru Swami Sri Bharati Krishna Trithaji projected the concept of this ancient methodology that became very popular to achieve high-speed processing of the data [5] [6]. As arithmetic operations are very important in the design of digital processors and application specific circuits, arithmetic circuits form an important class of circuits in digital systems. Multiplication is the scaling operation performed one number by another used frequently in various applications like convolution, Fast Fourier Transforms, Filters, ALU of Processors, etc. Hence the development of fast and accurate multipliers is necessary. ALU is an execution unit which not only performs the arithmetic operation, but also logical operation and therefore ALU is called as a heart of Microprocessor, Microcontroller, and CPUs.
The organization of the paper starts with a brief introduction and Section 1, proposes the steps approaching Vedic methodology. Section 2, illustrates Vedic Wallace Multiplier. Section 3, illustrates the designing of different multipliers based on the bit size, followed by a NxN Vedic Wallace Multiplier in Section 4. Furthermore, Section 5 focuses on the realization of the Vedic Wallace Multiplier unit in XilinxISE 14.5. Section 6 comprises the design of ALU, whereas an in-depth discussion of the important outcomes is included in Section 7. Finally, the conclusion in the last section.
The Sanskrit word “Veda” means house of knowledge and this gift that the Indians gave to the world, thousands of years ago and this knowledge is now currently employed in our global silicon chip technology of engineering. Vedic mathematics is used to solve the complex calculations involved in usual mathematics. This is so because, the Vedic formula is claimed to be based on the natural principles on which the human mind works, so typical to the typical calculation that can be performed by a normal person, and hence Vedic mathematic provides techniques to solve operations with a large magnitude number easily. It consents to incorporate the arithmetic rules along with high speed and easy implementation, thereby viable for a range of applications based on computing. This is a very interesting field and presents some effective algorithms which can be applied to various branches of engineering such as computing and digital system processing [4].
The Vedic multiplier is based on the algorithm named as “Urdhva Tiryakbhyam” sutra. Traditionally, this well-known sutra has been employed to multiply two given numbers in a decimal number system. In this work, the same idea is applied to the binary number system to make the proposed algorithm compatible with the digital hardware. It is a universal multiplication formula that can be used in for all multiplications. It literally means “Vertically and crosswise”. It is based on a novel concept through which the generation of all partial products can be done with the concurrent addition of these partial products. The algorithm is viable for multiplication of any two numbers exhibiting bit length equal to n. Since the partial products and their sums are calculated in parallel, the multiplier is independent of the clock frequency of the processor. The multiplier based on this sutra has the advantage that as the number of bits increases, gate delay, and area increases very slowly as compared to other conventional multipliers [9-14].
To illustrate this scheme, let us consider the multiplication of two decimal numbers 252x846 by Urdhva-Tiryakbhyam method as shown in Figure 1. The digits on both sides of the line are multiplied and added with the carry from the previous step. This generates one of the bits of the result and a carry. This carry is added in the next step and hence the process goes on. If more than one line is there in one step, all the results are added to the previous carry. In each step, least significant bit acts as the result bit and all other bits act as carry for the next step. Initially, the carry is taken to be zero.

Figure 1. Multiplication of Two Decimal Numbers: 252x846
In general, Wallace tree addition uses full adders to extensively reduce the partial products. When the critical path is compared between the critical path in 4 bit conventional and Vedic multiplier, for a 4-bit multiplier, 4 partial products will be generated, as shown in Figure 2 and are named as p0 to p3. For Wallace tree multiplier, a 3:2 reduction is used, so that the partial products are reduced from 4 to 3. The Delay in critical path is given by the addition of 3 full adder sums, 2 full adder carry, and half adder carry.
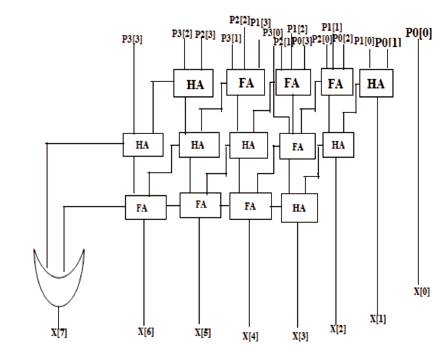
Figure 2. 4x4 Multiplier using Wallace Tree
The critical path for Vedic mathematics as shown in Figure 3, is given by 2FAS is reduced by 3HAS and in terms of XOR gates, Vedic-Wallace uses 3XOR gates instead of 4XOR i.e., less carry propagation delay than the conventional method. Hence, Vedic-Wallace has a variable improvement over design ware depending upon the number of bits in multiplication.
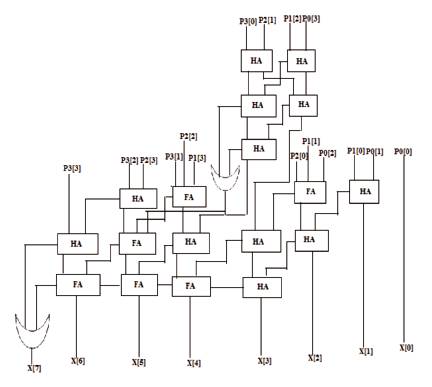
Figure 3. 4x4 Multiplier using Vedic Reduction
The hardware architecture of 2x2, 4x4, 8x8, 16x16, 32x32 bit Vedic Wallace multiplier (VW) modules are displayed in below sections. Here, “Urdhva-Tiryakbhyam” (Vertically and crosswise) sutra is used to propose such an architecture for the multiplication of two binary numbers. The beauty of Vedic Wallace multiplier is that, here partial product generation and additions are done concurrently. Hence, it is a well adapted parallel processing. The features make it more attractive for binary multiplications. This reduces delay and this is the primary motivation behind this work.
The method is explained for two, 2-bit numbers A and B where A=a1a0 and B=b1b0 as shown in Figure 4. Firstly, the least significant bits are multiplied which gives the least significant bit of the final product (Vertical). Then, the LSB of the multiplicand is multiplied with the next higher bit of the multiplier and added to, the product of LSB of the multiplier and the next higher bit of the multiplicand (crosswise). The sum gives the second bit of the final product and the carry is added to the partial product obtained by multiplying the most significant bits to give the sum and carry. The sum is the third corresponding bit and the carry becomes the fourth bit of the final product.
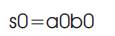

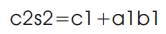
The final result will be c2s2s1s0. This multiplication method is applicable for all the cases. The 2x2 bit Vedic Wallace multiplier is implemented by using four input AND gates along with two half-adders. In the same way, 4, 8, 16, 32 and N bit multipliers are designed with a little modification.
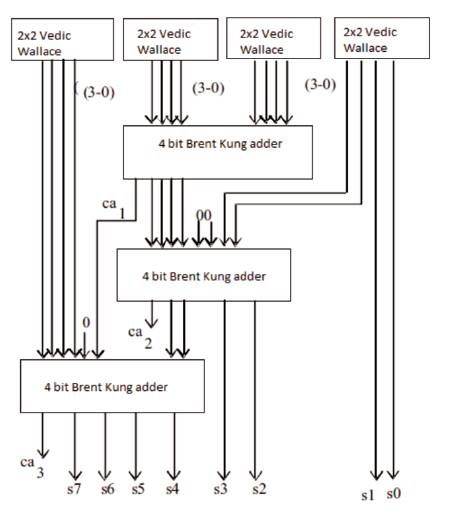
Figure 4. Schematic Diagram of 4x4 bit Vedic Wallace based Multiplier
The 4x4 bit Vedic Wallace multiplication unit is further realized by incorporating four similar modules of 2x2 multipliers. The processing in the form of a block diagram is depicted in Figure 4 for the 4x4 multiplier [8] .
The 8x8 Vedic Wallace Multiplier modules are realized using four 4x4 multiplier modules. The processing of 8x8 multiplier based on Vedic Wallace methodology is depicted in Figure 5. Demonstrating with an example of the two digits consisting of 8 bits, the output is obtained in 16 bits length.
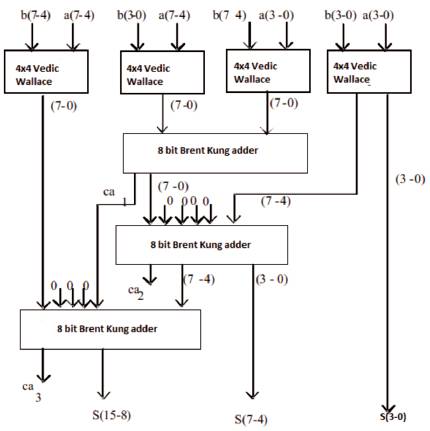
Figure 5. Schematic Diagram of 8x8 bit Vedic Wallace based Multiplier
The 16x16 Vedic Wallace Multiplier modules are realized using four 8x8 multiplier modules. The processing of the 16x16 multiplier based on Vedic Wallace methodology is depicted in Figure 6. Demonstrating with an example of two digits consisting of 16 bits, the output is obtained in 32 bits length.
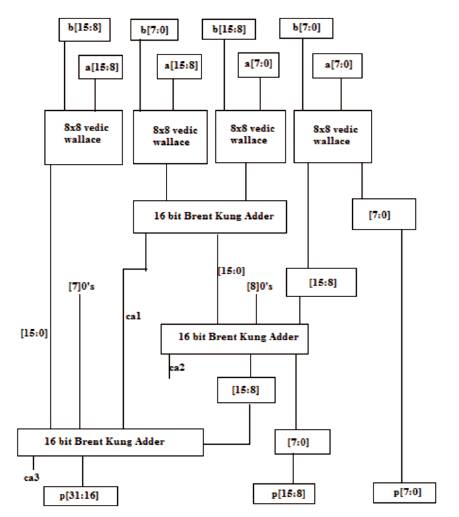
Figure 6. Schematic Diagram of 16x16 bit Vedic Wallace based Multiplier
The 32x32 Vedic Wallace Multiplier modules are realized using four 16x16 multiplier modules. The processing of 32x32 multiplier based on Vedic Wallace methodology is depicted in Figure 7. Demonstrating with an example of two digits consisting of 32 bits, the output is obtained in 64 bits length.
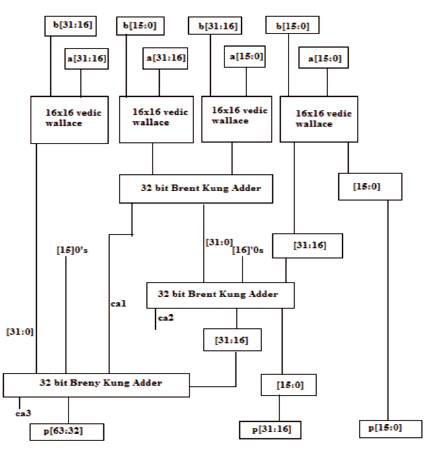
Figure 7. Schematic Diagram of 32x32 bit Vedic Wallace based Multiplier
The Schematic block diagram of NxN bit Vedic Wallace based Multiplier is shown in Figure 8.
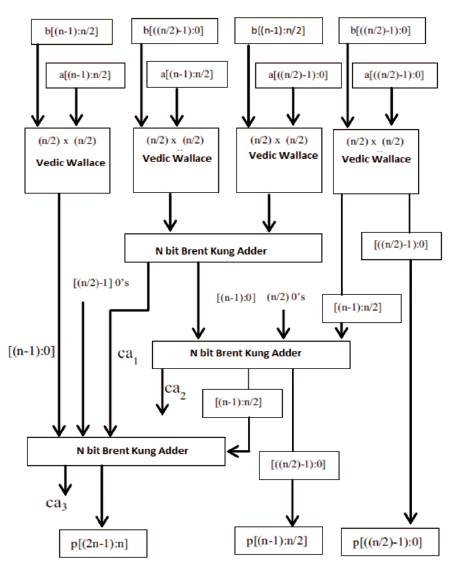
Figure 8. Schematic Block Diagram of NxN bit Vedic Wallace based Multiplier
This work begins out the realization of 32x32 Vedic Wallace multiplier by means of VHDL. Different abstractions units are synthesized with the help of Xilinx-ISE-14.5, the project navigator.
ALU was designed to perform the arithmetic and logical operations for the controller. Arithmetic operations performed are the 32-bit addition, subtraction, and multiplication. Logical operations performed are AND, OR, XOR, NAND, NOR, XNOR, NOT and Data Buffer. For designing the ALU, the authors had followed a flexible design that consists of smaller, but more manageable blocks, some of which can be re-used [2]. Designing of half-adder, 2-bit multiplier, 4-bit Brent-Kung, 4-bit multiplier, 8-bit Brent-Kung adder, 8-bit multiplier, 8-bit full adder, 8-bit subtractor, 32-bit Brent-Kung adder, 32-bit multiplier, 32-bit full adder, 32-bit subtractor, 32-bit arithmetic unit, logical unit and 32-bit ALU has been done [7].
For designing of the logical unit, the performance of logic circuits have been analyzed by employing the commonly used logic gates and a multiplexer. A Logic unit does the various operations such as Logical AND, OR, XOR, NOT, NAND, NOR, XNOR, and data buffer. In addition to this arithmetic unit and logical unit, they have been combined into the arithmetic logic units. The schematic block diagram of an arithmetic logic unit is shown in Figure 9, that is self-explanatory in itself. The output of the ALU and Logical Unit is 64 bits. Table 1 shows the control word for ALU operations.
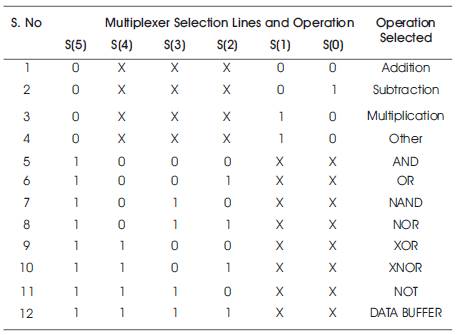
Table 1. Control Word for ALU Operations
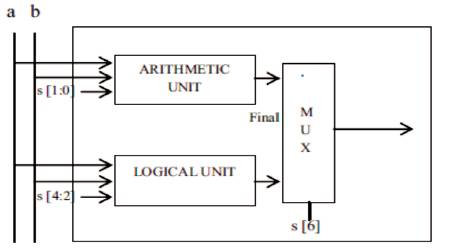
Figure 9. Schematic Block Diagram of Arithmetic Logic Unit
The proposed method has been simulated to find the lowest path delay for various multipliers. This section also deals with the quantitative and comparative result analysis of the different approach to Vedic mathematics through various multipliers and adder design and implementation. Additionally, to validate the proposed Vedic mathematics based various multipliers and adder designs and their implementation, the synthesis and the simulated results have been compared with some other trendy multiplier structures which are designed based on the different multiplication algorithms. Table 2, shows the efficacy of the proposed Vedic Wallace multiplier at 32- bit level. It has been compared and showed the lowest path delays in comparison to others. Figure 10 shows the schematic block diagram of 32-bit RTL implementation by using Vedic Mathematics, whereas, the simulation results of 32-bit multiplier based on the Vedic Wallace and 32-bit Arithmetic Logic Unit as per the control word are shown in Figure 11 and Figure 12, respectively. Besides this, Table 3, summarized the ALU with different multipliers and adders.
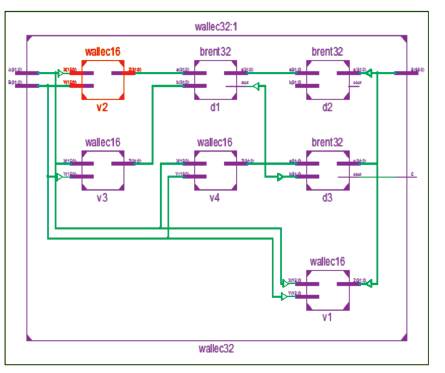
Figure 10. Schematic of 32-bit RTL Implementation using Vedic Wallace Multiplier

Figure 11. Simulation Results of 32-bit Multiplier based on Vedic Wallace
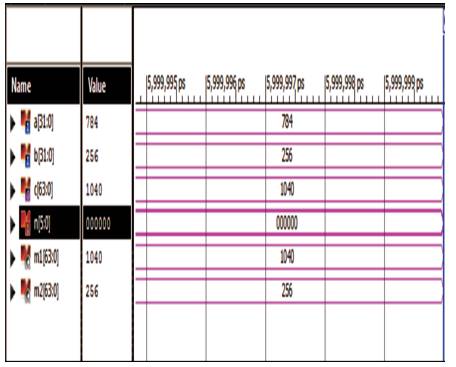
Figure 12. Simulation Results of 32 bit Arithmetic Logic Unit as per Control Word
Through this paper, the authors have presented an extremely effective method of multiplication, i.e. Urdhva- Tiryakbhyam Sutra based on Vedic mathematics. With this method, the multiplier of any number of bits can be designed, and show the computational benefits given by Vedic methods. It is a method for hierarchical multiplier design which clearly indicates the computational advantages offered by Vedic methods. Since the objective was to reduce the delay, the computational path delay for the proposed 32x32 bit Vedic Wallace multiplier is found to be 54.004ns. The Vedic Wallace multiplier is much more efficient than Vedic multiplier and Array multiplier in terms of execution time (speed) and Area Delay Product. So we can say Vedic mathematics can be included in the education systems and help students learn mathematics fast and perform better in less time. In future, all the research centers are to promote research works in Vedic mathematics.