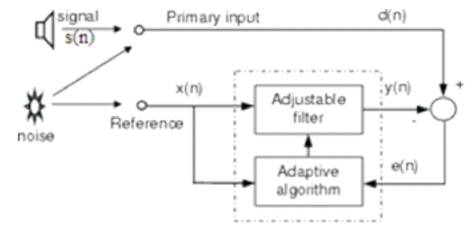
Figure 1. Simple Block Diagram of Adaptive Filter
This paper gives information about the comparison of adaptive filtering techniques like fixed LMS, Normalized Least Mean Square, and RLS for noise elimination in speech communication systems. The main objective of this paper is to suppress the additive noise which is due to the effect of environmental conditions in the communication systems. In these days, additive noise is one of the major problems in the communication, especially in the digital electronic circuit design. The origins of additive noise are because of atmospheric conditions, weather situations around the system and any other disturbances. Generally, the coefficients of filter updation in a basic filter does not occur time to time, as it may affect the desired information. By updating the coefficients of the filter time to time, this problem could be eradicated and thereby increasing the number of iterations for the filtering process, which gives efficient results. In the communication systems, the performance of these adaptive filters are in terms of mean square error, signal to noise ratio, rate of convergence, etc. In this research paper, the authors have discussed about how to cancel out the additive noise which is combined to the input speech signals that observes the records of signal to noise ratio, and mean square error. Finally, this article compares those results experimentally with the help of MATLAB programming and calculation tool. The mean square error improvement with the number of iterations for different noise signals are represented graphically. By the observation of the graphical results, the rate of convergence and reception level for the given speech and noise signals were found.
Adaptive filtering algorithms, which constitute the adjusting mechanisms for the coefficients of filter, are in fact closely related to classical optimization techniques although, in the latter, all calculations are carried out in an off-line manner [1]. Moreover, an adaptive filter, due to its real-time self-adjusting characteristic, is sometimes expected to track the optimum behavior of a slowly varying environment [2]. Noise is inevitable in any signal processing. Because of its common existence in every system, filters are introduced to eliminate these unwanted signals while retaining all the useful information signals. Generally, digital filters are more preferable than analogue filters, because it is easier to design and has more versatility in processing signals which includes the ability to adapt to the changes in the characteristics of the signals known as adaptive filters [3]. Due to its self-adjusting performance and in-built flexibility, adaptive filters are widely used in the areas of telephony, radar signal processing, navigational systems, biomedical signal enhancement and many more [4]. Adaptive noise or interference cancellation is one of the major useful adaptive systems and is the main focus of this project. In the digital signal processing, the useful data is represented in terms of bits, bytes, and can be indicated as ones and zeros. The main aim of the DSP is usually to measure, filter, and compress the continuous real-world analog signals and to convert them entirely into digital format without any interference at the reception side. In order to increase the signal to noise ratio, and decrease the mean square error, mostly two family of adaptive filters, namely recursive, non-recursive (LMS family) filters are used [5]. Most of the researchers are familiar with the least square adaptive filtering methods. Normalized LMS belongs to the family of non-recursive filters. LMS adaptive approach is also called as the Stochastic Gradient Approach [6-7]. This method calculates how much deviation occurs between the input and output. If the gradient between the input and output is small, then the output signal has a high signal to noise ratio [8]. The side lobe canceller is similar to the radio telescope array described by Erickson (1982), who has shown that a single interferer can be reduced to the noise level by post processing the data with an algorithm that first identifies a beam in the direction of the interference and then uses this beam to form a null in the array pattern [9]. The primary difference between Erickson's approach and the adaptive system is that, the adaptive filter performs the cancellation in real time and therefore requires no post processing [10-11]. The adaptive filters can track changes in the interference, while the post processing scheme assumes that the characteristics of the interference are quasistationary. The adaptive system analyzed in this report operates in the time domain, but as will be shown, the overall effect on the telescope is to reduce the interference through both temporal and spatial cancellation [12-13].
Least mean square filtering mechanism is the one of the familiar filtering mechanisms in the speech signal processing. In 1960, Windrow and Hoff had developed one of the most powerful algorithms called the Least Mean Square (LMS) algorithm. In this method, present output of the filter does not depend on the previous output. The general structure of LMS adaptive filter is as shown in Figure1.

Figure 1. Simple Block Diagram of Adaptive Filter
LMS algorithm is basically a nonlinear feedback control system. With the feedback known to be a “double-edged sword,” it can work for us or against us. It is not surprising, therefore, to find that with the control mechanism being directly dependent on how the step-size parameter, μ, is chosen. This parameter plays a critical role in assuring convergence of the algorithm (i.e., its stability when viewed as a feedback control system) or in failing to do so. The study of convergence is carried out under the umbrella of statistical learning theory of the LMS algorithm, which occupies a good part of this paper. Although, indeed, the LMS algorithm is simple to formulate, its mathematical analysis is very difficult to carry out. Nevertheless, ideas related to efficiency of the algorithm that are derived from this theory are supported through the use of Monte Carlo simulations. Using the adaptive transversal filter structure described in Figure 1, the upgrading of filter weights can be described by the following equations.
The updated filter weight equation is given below.
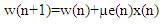
where,
w(n)=current weight of the filter,
μ = step size parameter,
s(n)= input speech signal,
x(n)=reference noise signal,
y(n)= w*x(n)= filter output, and
e(n)=d(n)-y(n)=reproduced speech signal at the receiver side.
Although behavior analysis of the LMS algorithm is beyond the scope of this work, it is important to mention that the step-size parameter plays an important role in the convergence characteristics of the algorithm as well as in its stability condition. In order to achieve the better stability, it must satisfy 0 < μ < 2λmax. In the point of view of rate of convergence, fixed LMS gives slower rate of convergence.
In order to avoid the drawback in the fixed LMS adaptive filter algorithm, ie, the changing the step size parameter μ causes a chance of degrading the parameter signal to noise ratio and increases the mean square error, the normalized LMS adaptive filter is the introduced. Here, the step size parameter is normalized using NLMS algorithm. In these algorithms, the selection of step size parameter μ is assumed in terms of α and c. Weight updation equation is given by,
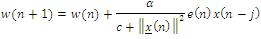
where || x (n) ||² is the squared Euclidean norm of the input x (n).
Here α is the adaption constant, which optimizes the convergence rate of the algorithm.
Range of alpha is: 0<α<2 and,
c is the constant term for normalization and always c<1.
NLMS algorithm gives a better performance when compared to the FIXED LMS adaptive algorithm.
In order to provide improvement in the signal to noise ratio, a highly recursive mechanism plays a vital role to suppress the noise content. The recursive mechanism states that the output of the filter is given to itself due to recurring process. In this paper, it is observed that when the signal to noise ratio is increased, the mean square error is reduced closely. The recursive filter is a filter in which the present output of the filter depends on the previous output also. This process can be understood from Figure 2.
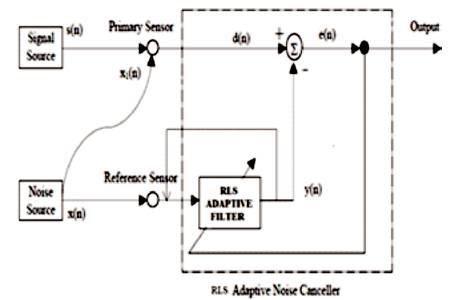
Figure 2. Structure of RLS Adaptive Filter
The RLS-type algorithms have a high convergence speed which is independent of the eigen value of the input correlation matrix. These algorithms are also very useful in applications where the environment is slowly varying. The price of all these benefits is a considerable increase in the computational complexity of the algorithms belonging to the RLS family.
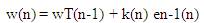
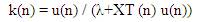
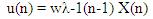
where λ is a forgetting factor, which value lies between 0 and 1.
In this paper, the comparison tables of the parameters regarding to signal processing for 3 different noise signals, namely voltage, crane, plectron and one speech signal combi1 have been analyzed. The program codes are simulated regarding to LMS, NLMS, and RLS adaptive filters using MATLAB R2010A version.
The Comparison tables are given below.
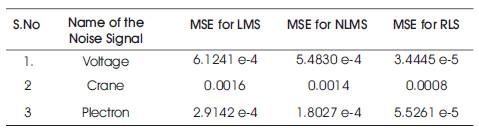
Table1. MSE Table for Different Noise Signals for N=16000 Iterations
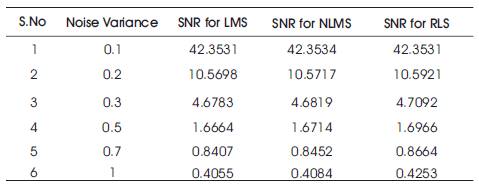
Table 2. SNR Table for Noise Signal and Combi1 Input Speech Signals
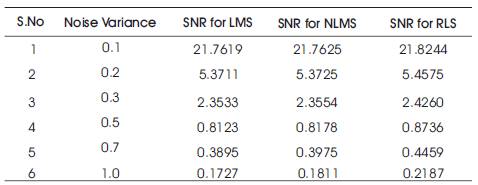
Table 3. SNR Table for Crane Noise Signal and Combi1 Speech Signal
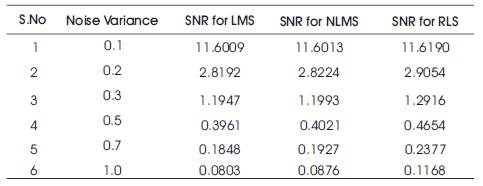
Table 4. SNR Table for Plectron Noise Signal and Combi1 Signal
From Table 1, it is observed that recursive least square algorithm provides a least mean square error and faster rate of convergence compared with LMS and NLMS algorithms.
SNR Comparison tables for different proportions of noise signals and combi1 speech signal are given in Tables 2, 3 and 4.
It is observed from Table 2, when the % of noise signal content increases, the signal to noise ratio becomes low.
From Table 3, it is observed that when the noise variance is small, the signal to noise ratio is high and the mean square error becomes less.
It is observed from Table 4, when the plectron noise variance is small, the signal to noise ratio is high and the mean square error is less. When the noise variance is high, the signal to noise ratio becomes low and the mean square error becomes high.
The graphical representation of MSE improvement with the number of iterations is shown in Figure 3 and it is observed that the mean square error curve of RLS algorithm is better compared to LMS and NLMS.
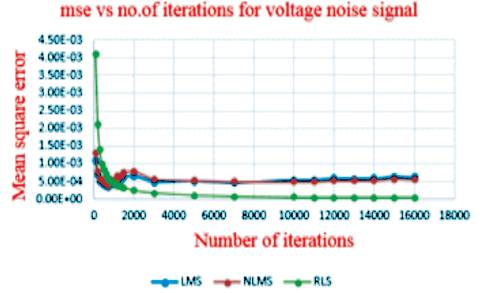
Figure 3. MSE Improvement Graph for Voltage Noise
The picture representation of decreasing the MSE values with the increase in the number of iterations is shown in Figure 4 and it is observed that mean square error curve of RLS algorithm is better compared to LMS and NLMS.
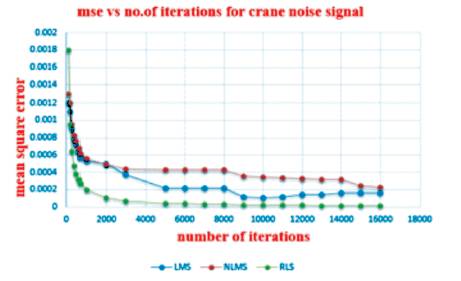
Figure 4. MSE Improvement Graph for Crane Noise Signal
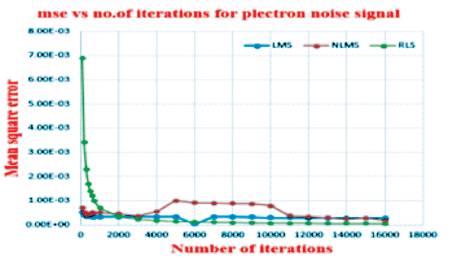
Figure 5. MSE Improvement Graph for Plectron Noise Signal
From Figure 5, the decrease in the MSE values with the increase in the number of iterations was observed. RLS algorithm gives very less MSE compared with the LMS, NLMS algorithms.
The noise eliminator in the digital signal processing is generated by the tool MATLAB. From this research, an idea to eliminate additive noise in the digital speech signal processing and implementation of adaptive noise cancellation by using some adaptive filter algorithm technique has been successfully achieved. It is also observed that, RLS adaptive filter algorithm technique is the best method to eradicate poor signal to noise ratio. Even though, highest number of iterations may take place and result in best valid signal to noise ratios, highest signal to noise ratio, and minimum mean square errors. From the results, it is observed that the mean square error, and the signal to noise ratios are improved and the rate of convergence has also increased. The simulation results show the efficiency of adaptive algorithms in the presence of three different noise signals. During the period of analysis of LMS, NLMS and RLS, it is concluded that the performance of RLS algorithm is better than both the LMS and NLMS adaptive algorithms for the desired speech and noise signals. RLS adaptive algorithm provides the best rate of convergence.