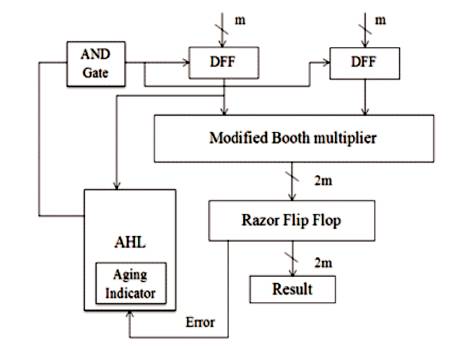
Figure 1. Block Diagram with AHL
Digital multipliers are most efficiently used in many applications such as Fourier Transform, Discrete Cosine Transforms, and Digital Filtering for high speed and low power consumption. The throughput of the multipliers is based on speed of the multiplier, and if it is too slow then, the entire performance of the circuit will be diminished. The pMOS transistor in negative bias cause Negative Bias Temperature Instability (NBTI), which increases the threshold voltage of the transistor and reduces the multiplier speed. Similarly, the nMOS transistor in positive bias cause Positive Bias Temperature Instability (PBTI). These effects reduce the transistor speed and the system may fail due to timing violations. So here, a new multiplier was designed with novel Adaptive Hold Logic (AHL) using Radix-4 Modified Booth Multiplier. By using Radix-4 Modified Booth Encoding (MBE), it is possible to reduce the number of partial products by half. Modified booth multiplier helps to provide higher throughput with low power consumption. This can adjust the AHL circuit to reduce the performance degradation. The expected result will reduce threshold voltage, increase throughput and speed and also reduce power. This modified multiplier design is coded by Verilog and simulated using Xilinx ISE 12.1 and implemented in Spartan 3E FPGA kit.
For Digital Signal Processing (DSP) like Fast Fourier Transform (FFT), Finite Impulse Response (FIR) filter, Discrete Cosine Transforms (DCT) etc., required high speed and low power Digital Multipliers. The throughput of these applications depend on multipliers and if the multipliers are too slow, the performance of entire circuits will be reduced. The Negative Bias Temperature Instability (NBTI) [7] occurs when a pMOS transistor is under negative bias (Vgs = −Vdd ). In this situation, the interaction between inversion layer holes and hydrogen-passivized Si atoms breaks the Si–H bond generated during the oxidation process, generating H or H2 molecules.
When these molecules diffuse away interface traps are left. The accumulated interface traps between silicon and the gate oxide interface result in increased threshold voltage (Vth ), reducing the circuit switching speed. When the biased voltage is removed, the reverse reaction occurs, reducing the NBTI effect. However, the reverse reaction does not eliminate all the interface traps generated during the stress phase and Vth is increased in the long term. Hence, it is important to design a reliable high-performance multiplier. The corresponding effect on an nMOS transistor is Positive Bias Temperature Instability (PBTI), which occurs when an nMOS transistor is under positive bias. Compared with the NBTI effect, the PBTI effect is much smaller on oxide or poly-gate transistors and therefore is usually ignored. However, for high metalgate nMOS transistors with significant charge trapping, the PBTI effect can no longer be ignored. The aim is to reduce the power consumption using Modified Booth Algorithm and increase the speed of the operation by reducing the threshold voltage of the multiplier. By using radix-4 Modified Booth Algorithm, partial products are reduced by half.
The throughput of the multiplier was increased. Reduce the threshold voltage and increase the drive current. Power consumption has been reduced. Also speed of the operation was improved. The modified reliable multiplier design with Adaptive Hold Logic helps to improve the throughput of the multiplier and also to reduce the threshold voltage and power consumption. Higher radix Modified Booth Algorithm and partial product reduction technique can give good result in terms of speed as well as area. By using Radix-4 modified booth algorithm, it reduces the number of partial products to half which improves the speed. An efficient multiplier should have following characteristics [2]: Accuracy- A good multiplier should give correct result. Speed- Multiplier should perform operation at high speed. Area- A multiplier should occupy less number of slices and LUT's. Power- Multiplier should consume less power.
For high-speed multiplication, the Modified Booth Algorithm (MBA) [5] is commonly used. For partial product reduction, different types of adders are used. Booth multiplication allows for the smaller, faster multiplication circuits through encoding the signed bits to 2's complement which is also the standard technique in chip design. Although the partial products are further reduced by using higher radix (2, 4, 8, 16, and 32), Booth Encoder increases complexity and improves the performance. By increasing radix value, partial products will be reduced. Hence, it will increase the speed. Low power consumption is also an important issue in multiplier design. To reduce significant power consumption, it is good to reduce the number of operation thereby reducing dynamic power which is a major part of total power consumption. So the need of high speed and low power multiplier has increased.
Andrea Calimera [1] et al. suggested a Negative Bias Temperature Instability (NBTI) effects on logic gates are of major concern for the reliability of digital circuits, they become even more critical when considering the components for which even minimal parametric variations impact the lifetime of the overall circuit. pMOS header transistors used in power-gated architectures are one relevant example of such components. In this brief, the authors address the problem of designing NBTItolerant power-gating architectures. They propose a set of efficient NBTI-aware circuit design solutions, including both static and dynamic strategies, that aim at improving the lifetime stability of power-gated circuits by means of oversizing, body biasing, and stress-probability reduction while minimizing the design overheads.
Jiang, H [5] et al. described an approximate multiplier with an approximate 2 bit adder is deliberately designed for calculating the sum of 1 and 2 of a binary number. This adder requires a small area, a low power and a short critical path delay. Subsequently, the 2 bit adder is employed to implement the less significant section of a recoding adder for generating the triple multiplicand with no carry propagation. In the pursuit of a tradeoff between accuracy and power consumption, two signed 16 bit approximate radix8 Booth multipliers are designed using the approximate recoding adder with and without the truncation of a number of less significant bits in the partial products. The proposed approximate multipliers are faster and more power efficient than the accurate Booth multiplier.
Cui. X [2] et al. described the conventional RB multiplier requires an additional RB partial product (RBPP) row, because an error correcting word (ECW) is generated by both the radix4 Modified Booth encoding (MBE) and the RB encoding. This incurs in an additional RBPP accumulation stage for the MBE multiplier. In this paper, a new RB Modified Partial Product Generator (RBMPPG) is proposed; it removes the extra ECW and hence, it saves one RBPP accumulation stage. Therefore, the proposed RBMPPG generates fewer partial product rows than a conventional RB MBE multiplier. Simulation results show that the proposed RBMPPG based designs significantly improve the area and power consumption when the word length of each operand in the multiplier is at least 32 bits; these reductions over previous NB multiplier designs incur in a modest delay increase (approximately 5%). The power delay product can be reduced by up to 59% using the proposed RB multipliers when compared with existing RB multipliers.
Jiun-Ping Wang [6] et al. suggested the fixed- width multiplier is attractive to many multimedia and digital signal processing systems which are desirable to maintain a fixed format and allow a little accuracy loss to output data. This paper presents the design of high-accuracy fixed-width modified Booth multipliers. To reduce the truncation error, we first slightly modify the partial product matrix of Booth multiplication and then derive an effective error compensation function that makes the error distribution be more symmetric to and centralized in the error equal to zero, leading the fixed-width modified Booth multiplier to very small mean and mean-square errors. In addition, a simple compensation circuit mainly composedof the simplified sorting network is also proposed. Compared to the previous circuits, the proposed error compensation circuit can achieve a tiny mean error and a significant reduction in mean-square error (e.g., at least 12.3% reduction for the 16-bit fixedwidth multiplier) while maintaining the approximate hardware overhead.
IChyn Wey [3] et al. described a reliable low power multiplier design by adopting Algorithmic Noise Tolerant (ANT) architecture with the fixed width multiplier to build the Reduced Precision Replica redundancy block (RPR). The proposed ANT architecture can meet the demand of high precision, low power consumption, and area efficiency. We design the fixed width RPR with error compensation circuit via analyzing of probability and statistics. Using the partial product terms of input correction vector and minor input correction vector to lower the truncation errors, the hardware complexity of error compensation circuit can be simplified. In a 12×12 bit ANT multiplier, circuit area in our fixed width RPR can be lowered by 44.55% and power consumption in the ANT design can be saved by 23% as compared with the state-of-art ANT design.
Srinivas K.B [10] et al. described that a bypassing logic will reduce dynamic power dissipation as well as signal propagation delay. The demand for electronic portable devices is gaining more attention in recent decades.
Portable devices are demanding for low power. Multiplier is the critical part of any arithmetic operation in many DSP applications. So it is essential to design multipliers that utilize less power and provide high speed of operation. One main aspect of low power design is to minimize switching activities to reduce dynamic power dissipation. Row and column bypass multiplier is a new design which reduces the switching activities with architecture optimization. The switching activity should not occur unnecessarily and it should be avoided by bypassing.
Surendran E.K.L [11] et al. described a new multiplier using modified Radix4 booth algorithm with redundant binary adder for low energy applications. Multipliers are the building blocks of high performance systems like FIR filters, Digital signal processors, etc., in which speed is the dominating factor. There are many multiplier architectures developed to increase the speed of algebra. Booth algorithm is the most effective algorithm used for fast performances. This works by introducing a high performance multiplier using Modified Radix4 booth algorithm with Redundant Binary Adder to get high speed. A comparative study of different booth algorithms in terms of power consumption, delay, and area, energy and energy delay product is also discussed in this work.
Ing-Chao Lin [4] et al. proposed an aging-aware multiplier design with a novel Adaptive Hold Logic (AHL) circuit. Digital multipliers are among the most critical arithmetic functional units. The overall performance of these systems depends on the throughput of the multiplier. Meanwhile, the Negative Bias Temperature Instability effect occurs when a pMOS transistor is under negative bias (Vgs = −Vdd ), increasing the threshold voltage of the pMOS transistor, and reducing multiplier speed. A similar phenomenon, positive bias temperature instability, occurs when an nMOS transistor is under positive bias. Both effects degrade transistor speed, and in the long term, the system may fail due to timing violations. Therefore, it is important to design reliable high-performance multipliers. The multiplier is able to provide higher throughput through the variable latency and can adjust the AHL circuit to mitigate performance degradation that is due to the aging effect. Moreover, the proposed architecture can be applied to a column- or row-bypassing multiplier.
More, T.V. [7] et al. described the switching activity of the component used in the design depends on the input bit coefficient. This means if the input bit coefficient is zero, corresponding row or column of adders need not be activated. If multiplicand contains more zeros, higher power reductions can be achieved. To reduce the switching activity is to shut down the idle part of the circuit, which is not in operating condition. Use of look up table is an added feature to this design. Further low power adder structure reduces the switching activity. Flexibility is another critical requirement that mandates the use of programmable components like FPGAs in such devices.
Prabhu, A.S. [8] et al. proposed a modified low power booth multiplier for high speed and low power applications. The design of a normal multiplier consumes most of the power in DSP processors. In order to reduce the power consumption of multiplier, the low power Booth recoding methodology is implemented by recoding technique. This booth decoder will increase the number of zeros in multiplicand. Booth multiplier has booth decoder to recode the given input to booth equivalent. Hence the number of switching activity will be reduced so the power consumption of the design can be reduced. The input bit coefficient will determine the switching activity of the component that is when the input coefficient is zero corresponding rows or column of the adder should be deactivated.
Rajput, R.P [9] et al. described a High Speed Modified Booth Encoder Multiplier for Signed and Unsigned Numbers. This paper presents the design and implementation of Signed Unsigned Modified Booth Encoding (SUMBE) multiplier. The present Modified Booth Encoding (MBE) multiplier and the Baugh Wooley multiplier perform multiplication operation on signed numbers only. The array multiplier and Braun array multipliers perform multiplication operation on unsigned numbers only. Thus, the requirement of the modern computer system is a dedicated and very high speed unique multiplier unit for signed and unsigned numbers. Therefore, this paper presents the design and implementation of SUMBE multiplier. The modified Booth Encoder circuit generates half the partial products in parallel. By extending sign bit of the operands and generating an additional partial product the SUMBE multiplier is obtained.
A new multiplier was designed with a novel Adaptive Hold Logic (AHL) circuit as shown in Figure 1. This multiplier includes two m-bit inputs (m is a positive number), one 2m-bit output, one Modified Booth Multiplier, 2m 1-bit Razor flip-flops, and an AHL circuit. The multiplier is able to provide higher throughput through the variable latency and can adjust the AHL circuit to mitigate performance degradation that is due to the aging effect. Moreover, the proposed architecture can be applied to a Modified Booth multiplier. The multiplier is based on the variablelatency technique and can adjust the AHL circuit to achieve reliable operation under the influence of NBTI and PBTI effects. This architecture is performed in 16-bit and 32-bit multipliers and also be easily extended to large designs.

Figure 1. Block Diagram with AHL
The modified booth multiplier is used to perform highspeed multiplications as shown in Figure 2. This modified booth multiplier's computation time and the logarithm of the word length of operands are proportional to each other. It is possible to reduce half the number of partial product. Radix-4 booth algorithm used here increases the speed of multiplier and reduces the area of multiplier. In this algorithm, every second column is taken and multiplied by 0 or +1 or +2 or -1 or -2 instead of multiplying with 0 or 1 after shifting and adding of every column of the booth multiplier.

Figure 2. Flow Chart for Modified Booth Multiplier
Thus, half of the partial product can be reduced using this booth algorithm. Based on the multiplier bits, the process of encoding the multiplicand is performed by radix-4 booth encoder.
Radix-4 Modified Booth Encoder performs the process of encoding the multiplicand based on multiplier bits. It will compare 3 bits at a time with overlapping technique. Grouping starts from the LSB, and the first block uses only two bits of the multiplier and assumes a zero for the third bit. The detection unit has one of the two operands as its input to decide whether the Booth encoder calculates redundant computations. The functional operation of Radix-4 booth encoder is shown in Table 1.

Table 1. Radix-4 Booth Encoding
In Radix-4 Modified Booth algorithm, the number of partial products reduced by half. For multiplication of 2's complement numbers, the two bit encoding using this algorithm scans a triplet of bits. To Booth recode the multiplier term, consider the bits in blocks of three, such that each block overlaps the previous block by one bit. Grouping starts from the LSB, and the first block only uses two bits of the multiplier. Figure 3 shows the grouping of bits from the multiplier term in modified booth encoding.

Figure 3. Grouping of bits from Multiplier Term
Each block is decoded to generate the correct partial product. The encoding of the multiplier Y, using the modified booth algorithm, generates the following five signed digits, -2, -1, 0, +1, +2.
Each encoded digit in the multiplier performs a certain operation on the multiplicand, X, as illustrated in Table 1.
A 1-bit Razor flip-flop contains a main flip-flop, shadow latch, XOR gate, and multiplier as shown in Figure 4. The main flip-flop catches the execution result for the combination circuit using a normal clock signal, and the shadow latch catches the execution result using a delayed clock signal, which is slower than the normal clock signal. If the latched bit of the shadow latch is different from that of the main flip-flop, this means the path delay of the current operation exceeds the cycle period, and the main flip-flop catches an incorrect result. If errors occur, the Razor flip-flop will set the error signal to 1 to notify the system to re-execute the operation and notify the AHL circuit that an error has occurred.
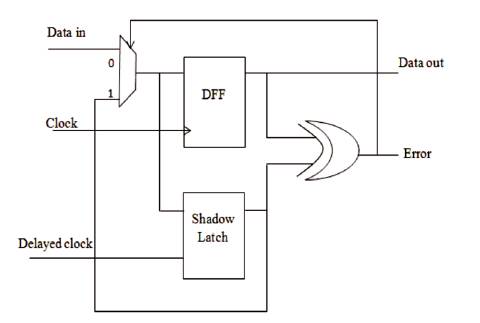
Figure 4. Razor Flip Flop
The authors use Razor flip-flops to detect whether an operation that is considered to be a one-cycle pattern can really finish in a cycle. If not, the operation is reexecuted with two cycles. Although the re-execution may seem costly, the overall cost is low because the re-execution frequency is low.
The AHL circuit contains an aging indicator, two judging blocks, one mux, and one D flip-flop as shown in Figure 5. The aging indicator indicates whether the circuit has suffered significant performance degradation due to the aging effect. The aging indicator is implemented in a simple counter that counts the number of errors over a certain amount of operations and is reset to zero at the end of those operations. If the cycle period is too short, Modified Booth Multiplier is not able to complete these operations successfully, causing timing violations. These timing violations will be caught by the Razor flip-flops, which generate error signals.
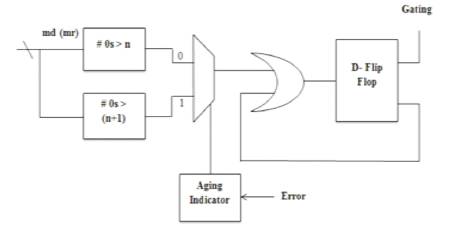
Figure 5. Adaptive Hold Logic (AHL)
If errors happen frequently and exceed a predefined threshold, it means the circuit has suffered significant timing degradation due to the aging effect, and the aging indicator will output signal 1, otherwise it will output 0 to indicate the aging effect is still not significant, and no actions are needed.
The first judging block in the AHL circuit will output 1 if the number of zeros in the multiplicand (multiplicator for the row-bypassing multiplier) is larger than n (n is a positive number), and the second judging block in the AHL circuit will output 1 if the number of zeros in the multiplicand (multiplicator) is larger than n + 1. They are both employed to decide whether an input pattern requires one or two cycles, but only one of them will be chosen at a time. In the beginning, the aging effect is not significant and the aging indicator produces 0, so the first judging block is used. After a period of time when the aging effect becomes significant, the second judging block is chosen.
Compared with the first judging block, the second judging block allows a smaller number of patterns to become one-cycle patterns because it requires more zeros in the multiplicand. When the modified booth multiplier finishes the operation, the result will be passed to the Razor flipflops. The Razor flip-flops check whether there is the path delay timing violation. If timing violations occur, it means the cycle period is not long enough for the current operation to complete and that the execution result of the multiplier is incorrect.
Thus, the Razor flip-flops will output an error to inform the system that the current operation needs to be reexecuted using two cycles to ensure the operation is correct. In this situation, the extra re-execution cycles caused by timing violation incurs a penalty to overall average latency. However, our proposed AHL circuit can accurately predict whether the input patterns require one or two cycles in most cases. Only a few input patterns may cause a timing variation when the AHL circuit judges incorrectly. In this case, the extra re-execution cycles did not produce significant timing degradation.
The simulation results for 8-bit booth multiplier using Radix- 4 Modified Booth algorithm is shown in Figure 6. By using Radix-4 Booth algorithm, the partial products are reduced by n/2. From Figure 6, 4 rows of partial products are only produced. Also delay has been analyzed. Then these partial products are added and produced the 16 bit multiplied output. From Figures 6 to 8, results have been obtained with the help of Xilinx 12.1 design suite.
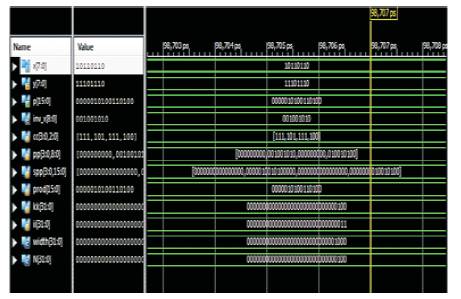
Figure 6. Simulation result for 8*8 Booth Multiplier
Figure 7 shows the output of Razor Flip Flop using D-Flip Flop and Shadow Latch simulated using Xilinx 12.1. The authors use Razor flip-flops to detect whether an operation that is considered to be a one-cycle pattern can really finish in a cycle. If not, the operation is reexecuted with two cycles. Although the re-execution may seem costly, the overall cost is low because the reexecution frequency is low
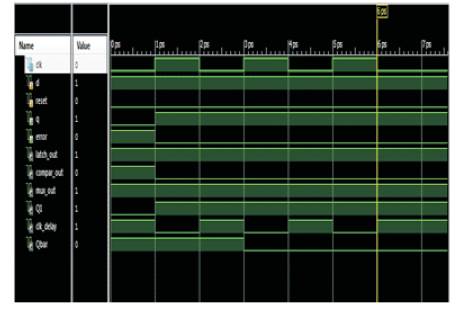
Figure 7. Simulation Result for Razor Flip Flop
Figure 8 shows the output of Adaptive Hold Logic using DFlip Flop simulated using Xilinx 12.1. The details of the operation of the AHL circuit are as follows: when an input pattern arrives, both judging blocks will decide whether the pattern requires one cycle or two cycles to complete and pass both results to the multiplexer. The multiplexer selects one of either result based on the output of the aging indicator. Then an OR operation is performed between the result of the multiplexer, and the Q signal is used to determine the input of the D flip-flop.
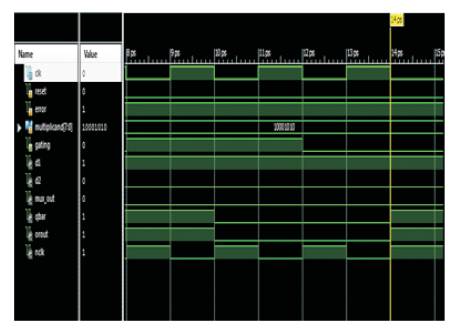
Figure 8. Simulation Result for Adaptive Hold Logic
High speed and low power multiplier design with Adaptive Hold Logic has been successfully simulated using Xilinx ISE Design 12.1. By using Radix-4 Modified Booth Algorithm, the number of partial products has been reduced by half, which improves the speed of the operation. In this architecture, we can improve the performance of the multiplier and also to improve the speed of the multiplier. By using Adaptive Hold Logic (AHL), the timing violation will be reduced and power consumption will also be reduced. So the overall performance will be improved.