There are numerous applications using different binary morphological operations reported in literature, e.g., noise Filtering, Boundary Detection, and Region Filling. The binary image representation can emerge not only due to the nature of the application, e.g., performing character recognition on a black and white document, but also as output from an Image Processing step, intensity thresholding, segmentation, or thresholded convolution. The existing binary morphology in [1];employs the image processing with MatLab simulation. Hence the synthesis could be done with DSP or ASIC architectures. Binary Image Processing is a powerful tool in many image and video applications [6]. Hence a reconfigurable processor is presented for binary image processing in this method

Image Processing plays vital role in the most demanding applications of Image and Video Processing. In general, importance is evident in diverse fields as Television Engineering. The importance of the Image Processing appears to be increasing with no visible sign of saturation. It is a mature technology domain wherein the demands for enhanced performance and reduced resource utilization have risen exponentially over the years.

Image Processing deals with the manipulation of digital signals using complex signal processing systems built from basic building blocks like filters and signal transformations. The advent of engineering tools has enabled the design of these basic building blocks faster and more accurate. Recent advancements in Field Programmable Gate Array (FPGA) synthesis technology, has resulted in this becoming the preferred platform for evaluating and implementing signal processing algorithms.

The computing units like FPGA architecture, like fast carry chains embedded multipliers, scalability and reconfigurability make it a very attractive platform for complex Image Processing algorithms.

Image-exogenous information - usually used to correct or to adapt an image anamorphism. Content dependent processing - contour preserving filters, and image restoration. The following techniques [2] have been introduced in this article: Fast Recursive Algorithms for Translation Invariant Structuring Elements. [3] Describes few algorithms and their hardware architectures for binary morphological erosion and dilation. And hence the stallfree low-complexity architecture is proposed that takes advantage of the morphological duality principle and Structuring Element (SE) decomposition. The complexity and number of memory accesses per pixel is low for both image and SE size common class of flat and rectangular SEs. [4] Provides en efficient blind binary image authentication scheme, whereas overall authentication and the second layer is targeted at identifying the tampering locations.

Morphological Image Processing (or morphology) described in [2] as a range of image processing techniques that deal with the shape (or morphology) of features in an image Morphological operations are typically applied to remove imperfections introduced during segmentation for the monochrome images. Morphological operators are used to prepare binary (threshold) images for object segmentation/recognition. Binary images often suffer from noise (specifically saltand- pepper noise) Binary regions also suffer from noise (isolated black pixels in a white region) and can also have cracks, picket fence occlusions. Dilation and erosion are two binary morphological operations that can assist with these problems.

2.1 Dilation

The basic effect of the operator on a binary image is to gradually enlarge the boundaries of regions of foreground pixels (i.e. white pixels, typically). Dilation is one of the two basic operators in the area of mathematical morphology, the other being erosion. Thus areas of foreground pixels grow in size while holes within those regions become smaller.

Figure. 1 Binary Morphological Image Processing Results. (a) Input Image. (b)dilation

The dilation operator takes two pieces of data as inputs. First issue is the image which is to be dilated. It is typically applied to binary images and hence it is noted that many versions work on grayscale images. The second is a set of coordinate points known as a structuring element. This structuring element determines the precise effect of the dilation on the input image.

Consider each of the background pixels in the input image in turn to compute the dilation of a binary input image by this structuring element. For all background pixel we superimpose the structuring element on top of the input image so that the origin of the structuring element coincides with the input pixel position. If a structuring element coincides with a foreground pixel in the image underneath, we can set the input pixel to the foreground value. If all the pixels in the image are background, the input pixel is left at the background value.

Dilation is the operation that combines two sets using vector addition of set elements. Dilation of image f by structuring element s is given by f ⊕ s.

The structuring element s is positioned with its origin at (x, y) and the new pixel value is determined using the rule:

[1]

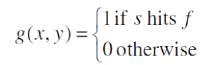
A binary image is viewed in mathematical morphology as a subset of a Euclidean space R^d or the integer grid Z^d, for some dimension d. Let E be a Euclidean space or an integer grid, and hence consider A as binary image in the space E, and structuring element is B.

The dilation of A by B is defined by:

[2]

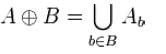
The dilation is commutative, also given by:

[3]

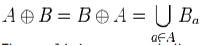
Figure 1(a) represents the original input image. Figure 1(b) denotes the dilated image.

2.2 Erosion

Erosion of image f by structuring element s is given by f ɵ s. The structuring element s is positioned with its origin at (x, y) and the new pixel value is determined using the rule:

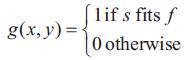
In binary morphology, an image is viewed as a subset of a Euclidean space R^dor the integer grid  Z^dfor some dimension d. The basic idea in binary morphology is to probe an image with a liberal determined image, whether this shape fits or misses the shapes in the image. This simple "probe" is called structuring element, and is itself a binary image (i.e., a subset of the space or grid).

The eroded image of A by the structuring element B is defined by:

[4]

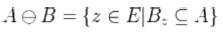
here translation of B is Bz by the vector z,

[5]

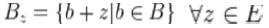
Figure 2(a) represents the original input image. Figure 2(b) denotes the eroded image.

Figure. 2 Binary morphological image processing results. (a) Input image. (b)Erosion

2.3 Opening

The opening of image f by structuring element s, denoted f ○ s is simply an erosion followed by a dilation

 

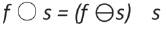
Where denotes erosion and denotes dilation. This process removes small objects from the foreground of an image. And then these objects are placing them in the background.

Figure 3(a) represents the original input image. Figure 3(b) denotes the result of morphological opening

Figure. 3 Binary Morphological Image Processing Results. (a) Input image. (b)Opening

The opening serves in computer vision and image processing as a basic workhorse of morphological noise removal. While closing removes small holes in the foreground, modifying small islands of background into foreground. Here usually small objects are taken as the dark pixels.

2.4 Closing

The closing of image f by structuring element s, denoted f s is simply a dilation followed by an erosion

[7]

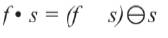
Where denotes dilation and denotes erosion.

In image processing, opening removes small objects whereas closing removes small holes.

Closing is employed in morphological processing for noise removal. It is a dual operator of opening; it can be derived from the fundamental operations of erosion and dilation. Closing is similar in some ways to dilation in that it tends to enlarge the boundaries of foreground (bright) regions in an image (and shrink background color holes in such regions). Here the fact is it is less destructive of the original boundary shape. It is an important operator from the field of mathematical morphology. Like those operators it is normally applied to binary images but there are gray level versions in operators. Figure 4(a) represents the original input image. Figure 4(b) shows the morphological closing.

Figure 4. Binary Morphological Image Processing Results. (a) Input image. (b)Closing

One of the uses of dilation is to fill in small background color holes in images. One of the problems with doing this is that the dilation will also distort all regions of pixels indiscriminately. This erosion on the image after the dilation will reduce some of this effect.

2.5 Hit-and-miss transform

Let A and B be two structuring elements. The pair (C,D) is sometimes called composite structuring element. For a given image A the hit-or-miss transform by B is given by:

[8]

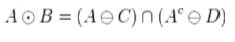
It is being used to construct the thinning and thickening operators often for all applications explained in these worksheets. The hit-and-miss transform has many applications in more complex morphological operations.

The Hit-and-miss operation is performed translating the origin of the structuring element to all points in the image. After this they are comparing the structuring element with the underlying image pixels. The foreground and background pixels in the structuring element exactly match foreground and background pixels in the image. It results in the pixel underneath the origin of the structuring element to be set to the foreground color. If it fails, then that pixel is set to the background color.

In order to generate the hard authenticator watermark, the key issue is how to locate the “embeddable” pixels given the watermarked image. When the block size (for both x and y directions), the non-interlaced 3X3 block becomes the fixed 3X3 block; the pattern of the determined pixels for the interlaced 3X3 block becomes the chess board patterns [5].

3.1 RSA algorithm

The RSA cryptosystem was invented by Rivest, Shamir, and Adleman in 1977. This is the most commonly used publickey cryptographic algorithm. It is considered as secure when sufficient long keys are used. The security of RSA depends on the difficulty of factoring large integers. Difficulty of factoring n to find the original primes p,q defines the strength of RSA. Hence the larger the value of primes, results harder in the factorization. Again, typical values for these primes are ranging from 512 to 4096bits. We can easily understand it from [11] the algorithm given below

1) Select any prime numbers p, q
2) Compute n = p*q
3) Compute ɸ = (p-1)*(q-1)
4) Select e, such that 1< e < ɸ, and gcd(ɸ, e) = 1
5) Find d such that ed = 1 mod ɸ
6) Public key KU = {e, n}
7) Private key KR = {d, n}

For any plaintext M < n,

Encryption, C = M e (mod n)

Decryption, M = C d (mod n)

We are doing the image encryption and decryption by using the above algorithm. Input image is written into one text file by using MATLAB. The text file is accessed by the VHDL code using MODELSIM and the processed the output values are stored in one another text file that is viewed by the MATLAB. Decryption has been developed by doing the same. We have to give the constant values n,e,d in RSA encryption and decryption.

Figure 5 represents the RSA cryptographic process. The bl ocks consist of the encoder/decoder and cryptographic modules.

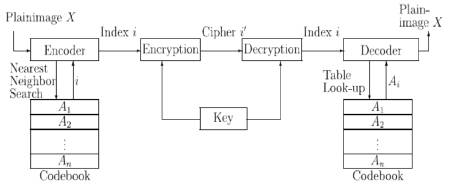
Figure 5. Cryptography Using RSA Algorithm

The modules of this article are used for segmenting a given image by morphological operations:

The initial step is to convert the given gray-level image into binary image. The one called "Label Binary Images" uses general threshold which makes the inside pixel equal to 1 and outside pixels equal to 0 and then creates a labeled binary image. The inside of the object is white and the outside is black. For converting a given image, in this project there are two modules integrated into Slicer 3. Here "Binary Threshold" thresholds the gray-level image by given upper and lower values in order to binarize the image. The inside pixels values are 255 and the ones which are in the outside of the object have the value 0.

For instance, in [7] we have two intersected spheres which are already binary image. After having binary image, the second step is performing erode operation to this image in order to make the different objects separate with the module called as Binary Erosion. In order to make them smooth, the spheres are threshold by general thresholding firstly and then by binary erode operation the spheres are totally separated to specify two different labels. Hence it is created by using Editor Module of Slicer 3.

The dilation operation is used in order to make them touch each other but not onto each other. The name of the module is Binary Dilation. The aim of this module is to make the totally separated objects touch each other but not overwritten. So the final step is to create the label map and make 3D model of touching but different labelled objects. The Editor and Model Maker modules are used in order to achieve this goal. The output of the algorithms is two different labelled binary images. This concept reflects the fact that images frequently contain collections of objects each of which can be the basis for a region. An image may be considered to contain sub-images sometimes referred to as regions-of-interest, ROIs, or simply regions. Thus one part of an image (region) might be processed to suppress motion blur while another part might be processed to improve color rendition. In a sophisticated image processing system it should be possible to apply specific image processing operations to selected regions.

Figure 6 represents the various modules in the mathematical morphological processing [8] . For digitization, the given Image is sampled on a discrete grid and each sample or pixel is quantized using a finite number of bits. Most usually, image processing systems require that the images be available in digitized form i.e., arrays of finite length binary words. Figure 7 represents the entity-relationship diagram. It provides the operations with the corresponding source codes.

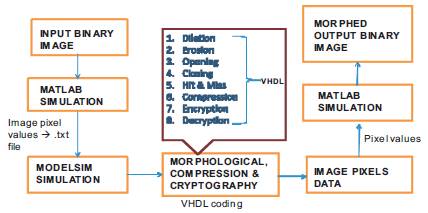
Figure 6. Binary Morphological Image Processing Modules

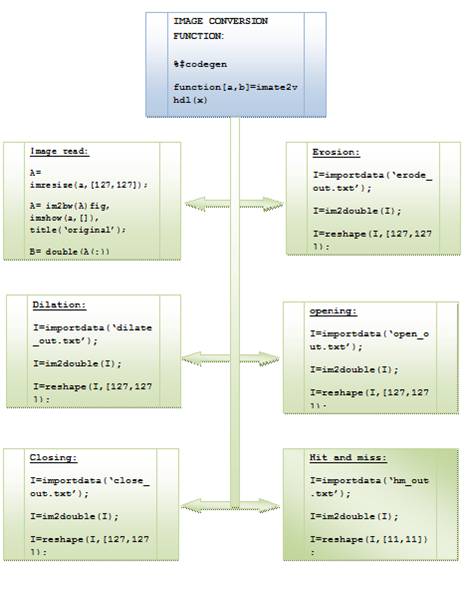
Figure 7. Entity– Relationship of Morphological Image Processing

To display a digital image, it is first converted into analog signal, which is scanned onto a display. The digitized image is processed by a computer [9] for videos.