During the last two decades extensive study on analytical/numerical method in the field of optical waveguide has been done by different researchers. Optical waveguides are the building blocks of photonics circuits. They are used as, couplers, switches, splitters, multiplexer and de-multiplexer for optical signals. Although the operation of waveguide devices is well known but their study on the performance characteristics which depends on many parameters like geometry, wavelength and initial field distribution, material data etc are still have a lot of scope to improve. These parameters must be optimized before fabricating a device. Optical fiber communication system requires the WDM optical network components. These components are often called non-uniform planar waveguide structure. In literature there would not found any straight forward analytical technique to analyze these components [1- 10]. One of such taper waveguide structure is shown in Figure 1 (a). This non-uniform waveguide structure or taper structure is divided into small steps discontinuity as shown in Figure 1(b). In next section the researchers will start by analyzing one such step discontinuity between m and m+1 steps. There is no mode conversion due to step discontinuity as such. The waveguide is designed to perform optimally for the fundamental mode only.

In this section the authors will analyze the power loss due to step discontinuity in an asymmetric planar slab taper waveguide structure. The dimension of structure is assumed to be small enough even at the point of discontinuity to be valid on single mode operation hence there is no chance of mode conversion. The analysis somewhat more involve in this case. One of such asymmetric waveguide structure with discontinuity is shown in Figure 2.

Figures 1(a) & (b). A taper waveguide structure has been divided into small steps

Here the n_f represents the film refractive index, n_s substrate refractive index and n_c cover refractive index. The three indices are chosen such that n_f > n_s > n_c and the guiding layers have a thickness 2a and 4a respectively in m^_th and m+ 1^th section. In the m^th region the wave solution is given by [2],

(1)

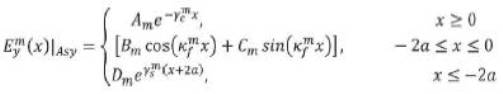
After applying the continuity conditions at various interface we get

(2)

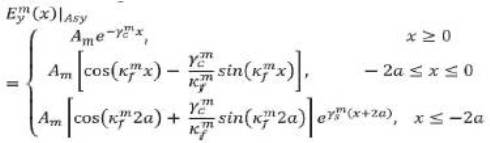
where A_m is the amplitude at the x = 0 interface and we get the following eigenvalue equation as

(3)

Similarly in the (m+1 )^th region the field solution is given by

(4)

continuity condition at x = a gives

(5)

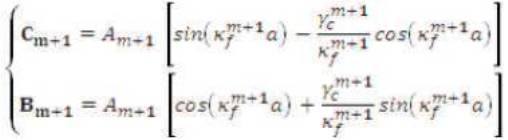
Similarly continuity condition at x = -3a gives

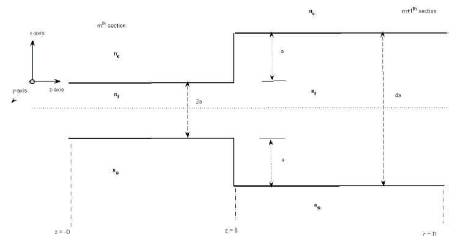
Figure 2. Step Discontinuity in Asymmetric Planar Slab Waveguide

(6)

after recombining of all these constants, we get

(7)

where A_m+1 is the amplitude at the x = 0 interface and after  boundary condition

(8)

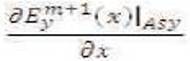
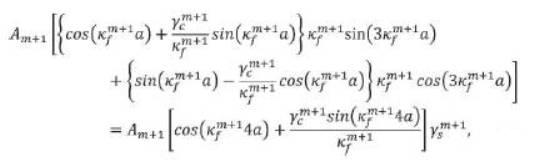
This can be further simplified to get

(9)

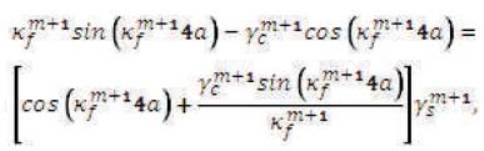
dividing by 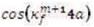both sides to get

(10)

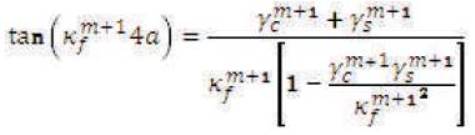
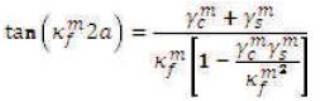
That is a transcendental equation derived for the (m+1)^th section having width of the film region 4a that must be solved numerically or graphically. In above equations (1) and (4) they assume that there are no reflections of the fields at the step discontinuity point. These two equations (3) and (10) can be simultaneously solved to get the exact values of K_m and K_m+1 . Consider the case when n_f= 1.49, n_s= 1.485, n_c= 1.45, a = 0.125 µm and operating wavelength The taper will support only one fundamental mode as shown in Figure 3. The values of βm are found 11.624µm^-1 and 11.647µm^-1 respectively; hence  β_m≈β_m+1[11-14].

Now if they consider the case when a = 0.75µm and other parameters remain same. Then taper will support multi modes as shown in Figure 4. Comparison of Figures 3 and 4 shows that a = 0.125µm give the single mode operation over a desired wavelength range[15].

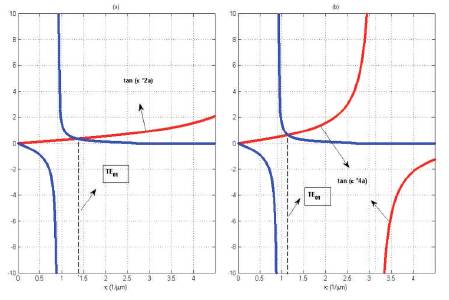
Figure 3. For Extremely Thin Asymmetric Taper Sections There is Only One Allowed Mode, Which Occurs at a) _Kf^m = 1.3496 µm^-1 b) K_f^m+1 = 1.1409 µm^-1

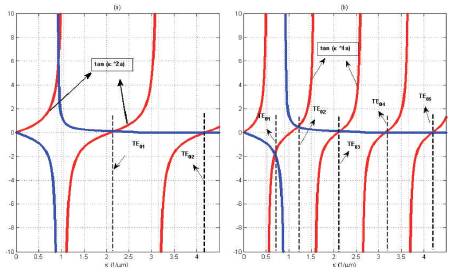
Figure 4. The Graphical Solution to the Eigenvalue Equation for a Multimode Asymmetric Waveguide Structure

By applying the similar procedure as for symmetric waveguide structure the continuity condition at

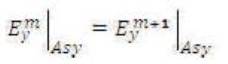
and

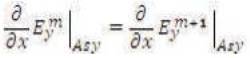at z=0

leads the following two equations [1]

(11)

(12)

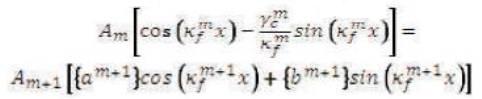
where

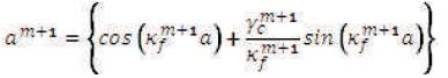
and

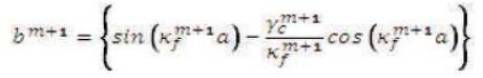
are the constants. Equations (11) and (12) can be simultaneously solved to get

(13)

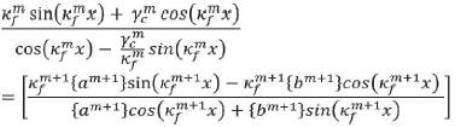
This equation is required for the graphical solution to know the optimum value of x for which eq. (13) will satisfy. The result is shown in Figure 5. It is apparent that maximum power will coupled from taper m^th section into m+1^th section only x≈-0.5µm Finally this condition will lead m [16-18],

(14)

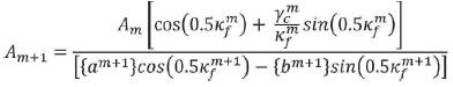
where K_f^m and K_f^m+1are measured in µ_m. By using condition (14) and after applying the continuity condition at step discontinuity point, we will get the following optimum equation

(15)

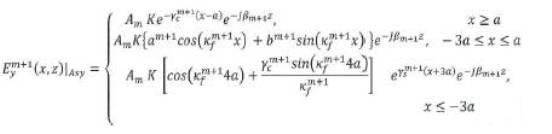
Here K is constant which can be easily evaluated and is given by,

(16)

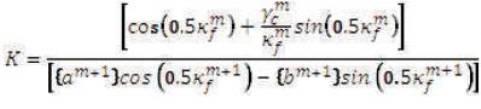
The unknown constant A_m can be found by normalizing the  input power to unit one which associated with the mode (per unit length in the y-direction) given by [20-24],

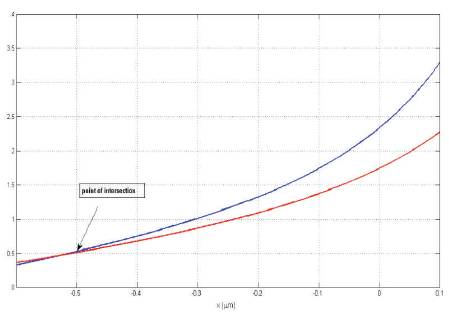
Figure 5. Optimum Power Coupling at Step Discontinuity Will Take Place Only if x ≈ -0.5µm (λ= 0.8µm)

(17)

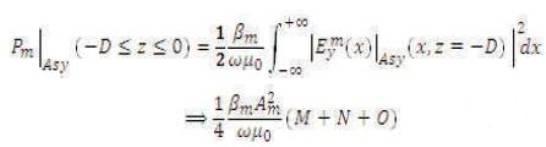
where

(18)

This power will remain constant till z = 0 point.

Power carried by fundamental TE₀₁ mode of m^th and (m+1)^th isolated sections is shown in Figure 6. Figure 7, shows the variation of constants A_m and A_m+1 (P_Total = 1) with wavelength. The fractional power carried by the film region of the m^thsection of asymmetric waveguide can be found by the expression

(19)

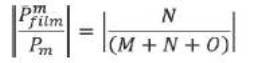
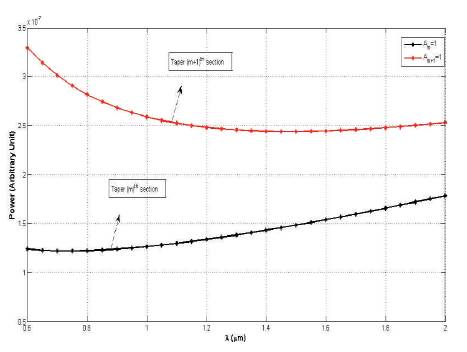
Figure 6. Power carried by m^th and ([m+1)]^th Isolated Sections

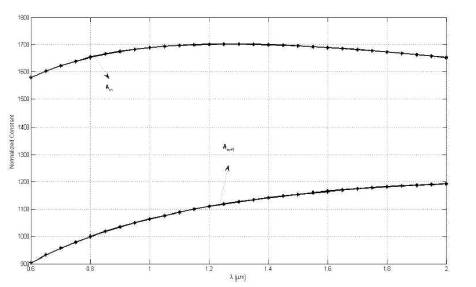
Figure 7. Calculated Normalized Constants A_m and  A_m-1 (P_Total = 1)

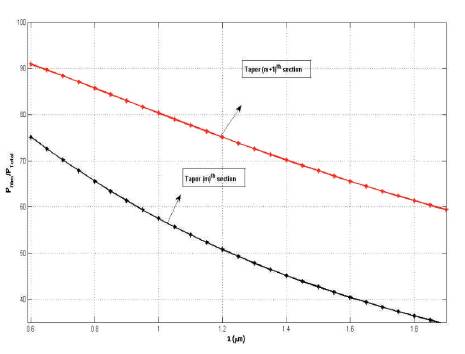
Figure 8. The Fractional Power (%) carried by the films of m^_th and ([m+1)]^_th Isolated Sections

The fractional power (%) carried by films region of m^th and ([m+1)]^th sections is shown in Figure 8. It shows that at lower wavelength the power confinement is large which saturates rapidly at higher wavelength region.

Now consider the taper discontinuity at z = 0. Then the power carried by (m+1)^th section of the taper can be described by

(20)

where

(21)

Figure 9 shows the effect of step discontinuity on power carried by m^th and (m+1)^th section. It reveals that there is substantial power loss due to discontinuity.

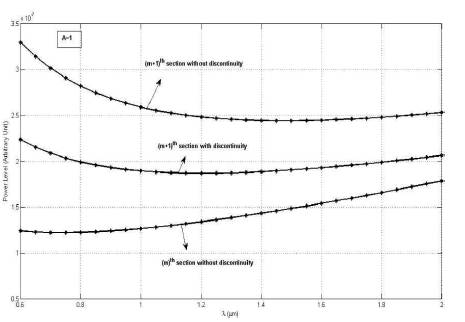
Figure 9. The Effect of Step Discontinuity on Power Carried by mth and ([m+1)]th Sections

Finally the power loss (%) due to discontinuity at z = 0 is given by

(22)

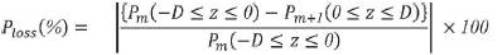
Figure 10 shows the power loss due to step discontinuity for various values of position x.

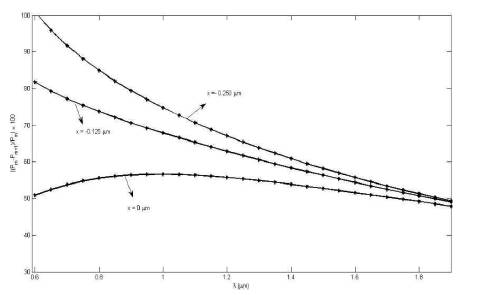
Figure 10. The Power Loss (%) Due to Step Discontinuity for Various Values of Position x (µm)

In this paper the authors have studied the effect of step discontinuity on single mode asymmetric planar slab taper waveguide structure. We found that the power loss due to step discontinuity is substantial. The results are found to be an accurate enough. The interpretations of the results are done at the end of the paper. By adopting the few assumptions the results have been derived. For more rigorous analysis of step discontinuity affect one need to consider the back reflection of the fields and mode conversion affect at the step discontinuity point. The technique presented in this paper is general can be easily extended to more complicated structure.