Figure 1. IEEE-754 Format for Double Precision Floating Point Numbers
In this paper, a high speed 64-bit double precision Floating Point Unit (FPU) using Vedic mathematics is proposed. In a general processor, the multiplication and division architectures play a crucial role in deciding the overall speed of the system. However, the standard algorithms are sequential units and reduce the performance of the processor. Vedic Mathematics on the other hand offers a new holistic approach of realizing these operations in a combinational unit. In the proposed architecture, the multiplication operation has been implemented using a 54-bit Vedic multiplier based on Urdhva Tiryagbhyam Algorithm while an optimized binary division architecture using Nikhilam Sutra is realized. The proposed method is coded in Verilog High Description Language (HDL), synthesized for Spartan 6 Field-Programmable Gate Array (FPGA) board and simulated using Xilinx Vivado Design Suite. An operating frequency of 205.08 MHz has been attained, which is 92.61% faster than the conventional implementation of a 64-bit floating point unit. The number of slice registers required for the overall realization of the FPU has also been reduced significantly by 94.3% and hence reducing the area requirement of the FPU in a general processor.
Floating point unit is a part of a processor specifically designed to perform operations on floating point or real numbers. An IEEE 754 double precision floating point format has been used for the representation of floating point numbers [3]. A floating point unit is widely used in the design of processors used in Automatic Control, Digital Signal Processing, Information processing, and application specific systems. Applications involving higher speed, accuracy, and precision necessitate the use of double precision floating point operations. Floating point representation has better resolution and accuracy compared to fixed point number representation.
The performance of any processor is defined by its power consumption, clock speed, and area requirement. For performing operations on floating point numbers, it is essential to have time and space competent techniques.
Vedic mathematics offers a combinational method to implement multiplication and division operations as opposed to the conventional techniques which are sequential [7]. Vedic mathematics is primarily established on sixteen sutras [5]. Among these sixteen sutras, Urdhva Tiryagbhyam algorithm is used to perform multiplication and Nikhilam sutra is used to perform division [2], [10]. By employing Vedic methodology, the operating speed of a floating point unit can be increased drastically. As the number of registers are also reduced, the overall area requirement of the processor is decreased.Hence the performance of a floating point unit and in turn a general processor is improved significantly due to the use of Vedic techniques.
The existing works on floating point unit have adapted the conventional methodologies for the arithmetic operations where division is performed through multiple subtractions [4]. As the partial results have to be stored in registers, a sequential circuit is realized. A logarithmic approach for performing the arithmetic operations on floating point numbers has been described in [9]. Although this approach reduces the complexity of computation and simplifies the overall data-path of the FPU, its memory occupancies lead to the latency in the model. In [6], the floating-point multiply-add units have been embedded in an island style FPGA. This technique has helped reduce the area and also improved the clock speed. But significant silicon wastage has also resulted from these embedded units in non-floating-point applications [6]. In this paper, the mantissa parts of the operands have been multiplied or divided using Vedic architectures and hence offer a dramatic improvement in clock rate.
This paper has been divided into five sections. The paper first briefly describes the IEEE-754 format for representation of double precision floating point numbers in Section 1. The standard floating point operations and their algorithms have also been explained in Section 2. The Vedic techniques for implementation of multiplication and division operations on 54-bit numbers are explained in Section 3. The simulation of the proposed architecture and itsperformance comparison is carried out in Section 4. Finally, conclusions are drawn in the Last Section.
For floating point computations, IEEE developed a standard format known as IEEE-754 [3]. The double precision format consists of 64 bits and is divided into three parts; 1 sign bit, exponential (11 bits), and mantissa (52 bits) as shown in Figure 1. The sign bit defines whether the number is positive or negative, 0 for positive and 1 for negative. The exponent value is offset by 1023. The mantissa also consists of a leading 1 for all double precision floating point numbers with exponential magnitude greater than 0. This leading 1 is not included in the 52 bits of mantissa.
Figure 1. IEEE-754 Format for Double Precision Floating Point Numbers
The IEEE-754 standard also defines five exceptions; Invalid, division by zero, overflow, underflow, and inexact. In the proposed floating point unit, these exceptions are indicated by output flag signals.
If the addition operation is selected and the operands are opposite in sign, the floating point unit computes the operation as subtraction. Similarly, if the subtraction operation is selected and the operands are opposite in sign, the floating point unit performs addition on the operands. The sign bit is computed in accordance with the magnitude of the operands. Figure 2 represents the flowchart for Addition and Subtraction
Figure 2. Flowchart for Addition/ Subtraction
In addition of two 64-bits double precision floating point numbers; two cases were considered - numbers with unequal exponents and numbers with equal exponents.
First two numbers A and B with unequal exponents are considered. After separation of the numbers A and B into their corresponding mantissas and exponents, four values man_A, exp_A, man_B, and exp_B are obtained. Next the exponents of the two are compared to get exp_large and exp_small. By the comparison of exponents, man_large and man_small are obtained. If the exponents are equal, man_large might have the smaller mantissa as only the exponent values is considered in assigning the small and large values. But in the next case, after obtaining the four values man_large, man_small, exp_large, and exp_small, shifting of the mantissa is performed.
Let the difference between the values of exp_large and exp_small be 'd'. The mantissa of smaller exponent, i.e man_small is shifted by d bits to the right. Let the new mantissa obtained be denoted by man_new_small. Then it is added to the mantissa of the other number (man_large). This addition is performed after including a leading 1 to both the 52 bits mantissas for normalization. The man1_small is 53 bits of d bits right shifted man_small (including a leading 1) and man1_large is 53 bits of the mantissa of the number with larger exponent (including a leading 1). Resultant mantissa is res_man= man1_small + man1_large and resultant exponent is rs_exp= exp_large.
If the exponents of the two numbers are equal, a leading 1 is included in front of each mantissa and an extra 0 in front of the 1 in case the addition overflows. Because when an overflow occurs, the exponent must be increased by 1. The resultant mantissa is res_man= man_1+man_2, which is 54 bits (including the leading 0 and 1). After the th addition, the 54 bit gets shifted out of the result and can be used for rounding purposes later. The leftmost 1 can become the leading 1 of the resulting mantissa.
Similar to addition, two numbers with unequal exponents are considered. After separation of the numbers A and B into their corresponding mantissas and exponents, four values man_A, exp_A, man_B, and exp_B are obtained. Next the exponents of the two are compared to get exp_large and exp_small. By the comparison of exponents, man_large and man_small is also obtained. If the exponents are equal, man_large might have the smaller mantissa as only the exponent values is considered in assigning the small and large values. After obtaining the four values man_large, man_small, exp_large, and exp_small, shifting of the mantissa is performed. Let the difference between the values of exp_large and exp_small be 'd'. The mantissa of smaller exponent, i.e man_small is shifted by d bits to the right. Let the new mantissa obtained be denoted by man_new_small. In case the exponents are equal, the mantissas are subtracted without any right shift of the mantissa.
The resultant mantissa after the subtraction is denoted by 'diff'. The number of 0s in diff before the leftmost 1 is counted, let the number of zeros be num. Now, the exponent of the larger operand is reduced by num and the result is left shifted by num number of bits to obtain the mantissa of the answer. The leftmost 1 of diff becomes the leading 1 of the resulting mantissa.
The sign of the result is obtained by XORing the sign bits of the two operands. Next, the exponents are added and 1023 is subtracted from the result to obtain the resultant exponent. A leading 1 is added to both the mantissas to obtain 53 bit man_A and man_B which are multiplied using the 54-bit Vedic multiplication module based on Urdhva Tiryagbhyam Algorithm as explained in the next section. Hence a 106 bit product is obtained Figure 3 shows the architecture for floating point multiplication
Figure 3. Architecture for Floating Point Multiplication
For normalization, if 105 bit of result is 1, mantissa is normalized to 52 bit by taking 104 to 53 bit position number and exponent is increased by decimal value one. If 105 bit of result is 0, mantissa is normalized to 52 bit by taking 103 to 52 bit position number and there is no increment in the exponent value.
Firstly, a leading 1 is added to mantissas of both the operands to obtain a 53 bit divisor and a 53 bit dividend.
The two mantissas with leading 1 are divided using a 54-bit Vedic divider module based on Nikhilam Sutra as explained in the next section. The resulting mantissa is normalized to 52 bits. Figure 4 represents the architecture for floating point division.
Figure 4. Architecture for Floating Point Division
A 54 bit quotient is obtained from the 54 bit Vedic Divider Module. If the most significant bit of the quotient is 1, nd st mantissa is normalized to 52 bit by taking 52 to 1 bit position number and exponent is increased by decimal rd value one. If 53 bit of result is 0, mantissa is normalized to th 52 bit by taking 51 to 0 bit position number and there is no increment in the exponent value.
To obtain the resultant exponent, exp_small is subtracted from exp_large and 1023 is added to the result to obtain result_exp. If the result_exp is less than 0, the quotient will be right shifted by the magnitude. The sign bit is obtained by XORing the sign bits of the two operands.
In this paper, all the four rounding modes specified by the IEEE 754 standard have been defined. The user has the liberty to choose the desired rounding mode. The four rounding modes are:
The output signals of underflow, overflow, inexact, exception, and invalid arein accordance with the IEEE 754 standard. The special cases have been described in Table 1. If any of the below cases occur, exception signal is asserted.
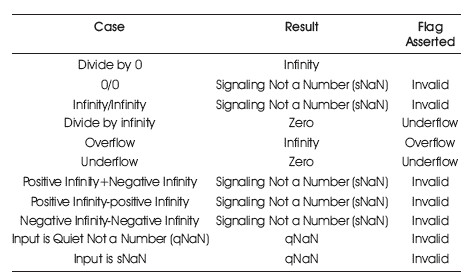
Table 1. Cases for Exception Signals
The Vedic technique for multiplication of two 54 bit unsigned numbers using Urdhva Tiryagbhyam sutra has been demonstrated in this section. The mantissa part of a double precision floating point number along with its leading 1 constitutes 53 bits. The mantissa parts of the two operands need to be multiplied using an unsigned multiplier. The word Urdhva Tiryagbhyam signifies vertical and crosswise [6]. This methodology is implemented by computing partial products and subsequent addition.
The delay and area of the architecture of a Vedic multiplier increases gradually with the number of bits of the operands in comparison to conventional multipliers.
A 3-bit Vedic multiplier is used as a fundamental block for the 54-bit multiplier. For multiplication of 3-bit binary numbers, consider two operands x and y. x can be denoted as x x x and y as y y y . As shown in Figure 5, x 2 0 and y are multiplied and stored as s =x y . For cross multiplication, x is multiplied with y and y is multiplied with x . The partial results are added together and stored as c s =x y + y x . Similarly, c s = c + x y + x y +x y ; c s =c +x y +x y and c s =c +x y . The final product is computed as c s s s s s . Using the 3-bit Vedic multiplier as 4 4 3 2 1 0 a fundamental block, a 54*54 Vedic multiplier is implemented. The architecture of the proposed 54-bit multiplier is shown in Figure 6. Carry save adder is used for the summation of partial products. The final product is of 108 bits which is normalized to a 52 bit mantissa using the normalization procedure explained in the section above.
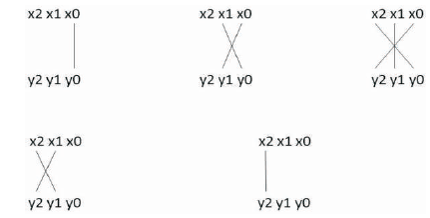
Figure 5. Vedic Multiplication of two 3-bit Numbers
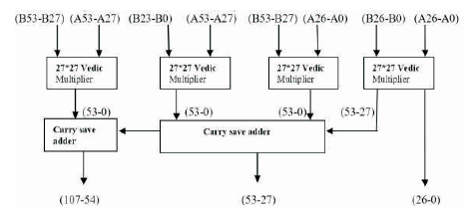
Figure 6. Vedic Multiplication Architecture for 54-bit Binary Numbers
Table 2 compares the combinational time delay between an array multiplier and a Vedic multiplier for 2, 4, and 8 bits [1]. As can be observed from the table, vedic multiplier is faster than array multiplier for all the three cases. The difference in the time delay between the two multipliers increases as the number of bits is increased.
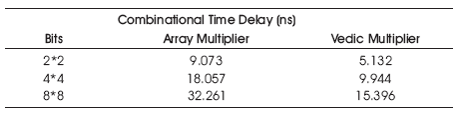
Table 2. Delay Comparision of Vedic Multipler [1]
The Nikhilam Navatascaramam Dasatah sutra literally means 'all from 9 and the last from 10' [8]. Division algorithm using Nikhilam Sutra utilizes only addition and complement operations. The mantissas of the two operands are divided using a 54 bit Vedic divider based on Nikhilam Sutra.
The proposed architecture for 54-bit divider using Nikhilam sutra is shown in Figure 7. Consider A as dividend and B as divisor. B is fed as input to the circuit of two's complement operation. The two's complement of B is multiplied with the most significant 27 bits of A. The same 27 bits of A are also given as input to an incrementer initialized by 0. The product of multiplication is summed with the 27 LSB of A. If the sum is greater than B, the sum is again fed as input to the multiplier replacing A [54:27]. The operation is reiterated until the sum is less than the divisor B. The result of the incrementer is the quotient of the division. The quotient is normalized to 52 bits and forms the mantissa of the final output.
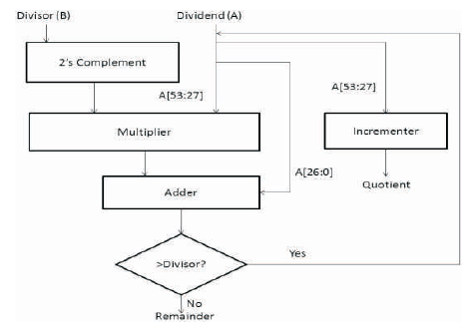
Figure 7. Flowchart for Nikhilam Sutra
The architectural schematic of 64 bit double precision floating point unit using Vedic mathematics was synthesized using Xilinx Vivado Design Suite for Spartan 6 FPGA board. Vivado Design Suite is a software suite developed by Xilinx for synthesis and analysis of HDL designs. Verilog HDL has been used for the design of the proposed floating point unit. Spartan 6 was specifically chosen as to compare the performance of the FPU based on speed and area with the existing work [6] under the same conditions. The maximum frequency achievable by a clock in an FPGA board is defined by its speed grade. The speed grade of Spartan 6 FPGA board chosen is -3. The design has been verified by simulation using ISIM Simulator. The synthesized Register-Transfer Level (RTL) schematic has been shown in Figure 8. The synthesis report generated by Xilinx Vivado provides information on the maximum clock frequency, minimum clock period, and the number of slice Registers as tabulated in Table 2. Figures 9-12 represent the simulation results for 64-bit Addition, Subtraction, Multiplication, and Division.
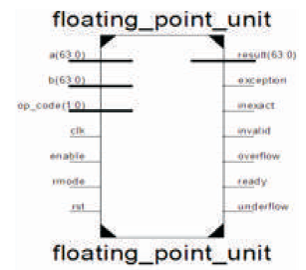
Figure 8. RTL Schematic of FPU
Figure 9. Simulation of 64-bit Addition
Figure 10. Simulation of 64-bit Subtraction
Figure 11. Simulation of 64-bit Multiplication
Figure 12. Simulation of 64-bit Division
This section verifies the operation of the FPU for four mathematical operations; addition, subtraction, multiplication, and division. Signals a and b are the 64 bit operands and a two bit signal op_code selects the desired operation. The result is stored in the 64 bit signal result. As shown in Figure 8, error signals exception, inexact, invalid, overflow, and underflow are also generated in accordance with IEEE-754 standard.
As tabulated in Table 3, the performance of the proposed architecture has been compared with the conventional implementation of a 64 bit floating point unit [4]. The existing work does not integrate the use of Vedic mathematics in its operations. The results show the maximum clock frequency achieved is 205.08 MHz which is 92.61% faster than its conventional counterpart. This increase in speed can be attributed to the use of Vedic techniques for multiplication and division operations. As the Vedic architecture is purely combinational as opposed to the conventional methods of multiplication
Table 3. Performance Comparison
and division which are sequential units, the number of slice registers essential for the implementation of floating point unit has been significantly reduced by 94.3%. The area requirement of the floating point unit has thus been condensed which makes it more economical.
In this paper, a more efficient IEEE-754 double precision Floating point unit based on Vedic techniques is proposed. The multiplication operation is realized using 54-bit Vedic multiplier based on Urdhva Tiryagbhyam Algorithm and the division operation is based on Nikhilam Sutra. The unit has been coded in Verilog HDL, synthesized for the Spartan 6 FPGA board using Xilinx Vivado Design Suite. The proposed architecture outperforms its counterpart in terms of clock speed by 92.61%. Accredited to the use of Vedic Sutras, the proposed work is improved with respect to speed, area, and accuracy. The design attained a maximum clock frequency of 205.08 MHz. The synthesized design can be further implemented on an FPGA board to confirm its operation and analyze its performance in terms of power dissipation.