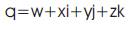
In this paper, the authors first discuss the quaternion representation of colour images and quaternion matrix algebra. Colour images consisting of the three RGB channels can be represented using pure quaternion-valued pixels. Then, to perform the decomposition of such colour images, they introduce the singular value decomposition of a quaternion matrix which represents a colour image. Finally, based on this decomposition they proposed a method for colour image compression without separating the colour image into three channel images. Results of the compression on three different colour images are presented.
The concept of the quaternion was introduced by Hamilton in 1843[1]. It is the generalization of a complex number. A complex number has two components: the real and the imaginary part. The quaternion, however, has four components, i.e., one real part and three imaginary parts and can be represented in Cartesian form as:
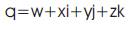
where w,x,y and z are real numbers and I, j and k are complex operators which obey the following rules.
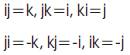
and also satisfies i2 =j2 =k2 =ijk=-1. From these rules, it is clear that quaternion multiplication is not commutative. The quaternion conjugate is
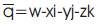
and the modulus of a quaternion is given by
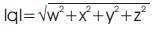
A quaternion with zero real part is called a pure quaternion and a quaternion with unit modulus is called a unit quaternion. Each quaternion q=w+x.i+y.j+z.k can be decomposed into a form as complex numbers i.e., q=(w+x.i)+(y+z.i).j=a+b.j where a and b are two complex numbers. Suppose we have an n x n quaternion valued matrix,Q with, Q=Ac +Bc .j. where Ac and Bc are n x n complex matrices, then the equivalent 2n x 2n complex matrix C of Q is
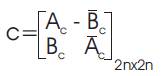
By converting Q into complex matrix representation C, the classical complex SVD algorithm can be applied to C to generate the eigen-basis (eigen vectors) and corresponding singular values ranked in descending order (all singular values are real).
In this paper, the authors focus on the quaternion matrices and they use concept as in [2] to calculate the eigen values of the quaternion matrix and to compute the SVD of a quaternion matrix. Based on this quaternion singular value decomposition, they propose a new method for colour image compression without separating the colour image into three channel images. The main advantage of this method compared to conventional colour image compression approaches is that it does not require separation of colour image into three channel images and also provides good quality reconstructed images even for extreme compression ratios. The quaternion arithmetic involved in various operations is implemented using the quaternion toolbox for Matlab[5].
The remainder of this paper is organized as follows. In section 1, the authors discuss the quaternion representation of colour image pixels. Using quaternions to represent colour images is done by encoding the three channels into the three imaginary parts of a pure quaternion. Section 2 deals with decomposition of a quaternion matrix which represents a colour image based on quaternion principal component analysis such as quaternion singular value decomposition and section 3 deals with colour image compression based on this decomposition. Section 4 gives the results of compression. Section 5 concludes the paper.
Colour image pixels have three components, and they can be represented in quaternion form using pure quaternions[3], [6] [7] [8]. For images in RGB colour space, the three imaginary parts of a pure quaternion can be used to represent the red, green and blue colour components. For example, a pixel at image coordinates (x,y) in an RGB image can be represented as
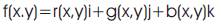
where, r(x,y), g(x,y), and b(x,y) are the red, green and blue components of the pixel, respectively. Figure1 illustrates the approach adopted to represent RGB colour image using the quaternion form.
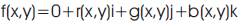
Using quaternions to represent the RGB colour space, the three colour channels are processed equally in operations such as multiplication. The advantage of using quaternion based operations to manipulate colour information in an image is that we do not have to process each colour channel independently, but rather, treat each colour triple as a whole unit. The authors believe, by using quaternion operations, higher colour information accuracy can be achieved because a colour is treated as an entity.

Figure 1. Quaternion Representation of a Colour Image.
The following section reviews the Quaternion Principal Component Analysis (QPCA). The implementation of QPCA is based on the Quaternion Singular Value Decomposition (QSVD).
The singular value decomposition is an important technique in linear algebra. It plays an interesting, fundamental role in many different applications, for instance, in digital image processing. The singular value decomposition of a matrix factors an m x n matrix A into the form,
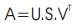
where U is an m x m orthogonal matrix; V an n x n orthogonal matrix, and S an m x n matrix containing the singular values of A with σ1 ≥ σ2 ≥ .... ≥ σn ≥ 0 along its main diagonal.
If we use quaternion-valued matrix Q to represent a colour image, where each pixel is represented by a pure quaternion, then by QSVD, the image can be can decomposed as
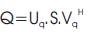
where Uq and Vq are two unitary quaternion matrices, S is singular matrix of Q and H represents the quaternion Hermitian transpose operator, or conjugate–transposition operator. The quaternion singular value decomposition (QSVD) can be considered as a generalization of real or complex number singular value decomposition, and inherits similar properties. Many papers have proposed how to compute the eigen-values of a quaternion-valued matrix[2],[4]. Ever y quaternion matrix can be decomposed into the multiplication of two matrices, Q and R, where Q is a unitary matrix and R is an upper triangular matrix. Therefore, a quaternion matrix can be decomposed into its singular value form by converting it into complex matrix representation.
Each quaternion matrix has an equivalent complex matrix. The relations (isomorphism: C <=> Q, where Q represents a quaternion number and C represents its complex equivalence) between the quaternion matrix and its equivalent complex matrix can be found in[2]. Therefore, the existing complex SVD algorithm can be applied to this equivalent complex matrix to obtain the eigenvectors and singular values of the corresponding quaternion matrix. In this paper, the authors use the approach as in[2] to calculate the eigen values of the quaternion matrix and to compute the SVD of a quaternion matrix.
The algorithm to compute the SVD of a quaternion matrix can be broken down into the following steps.
Step 1: Convert the input RGB colour image into a 2-D quaternion-valued matrix (Q).
Step 2: Calculate the equivalent complex matrix C of Q by Eq. (4).
Step 3: Compute the SVD of the complex matrix C by the conventional SVD of a complex matrix.
Step 4: The singular matrix S of Q and the two unitary quaternion matrices Uq and Vq can be computed by following the approach in [2].
Based on SVD of a colour image, many useful image processing methods by SVD can be extended to colour images without separating the colour image into three channels. Here, they use QSVD for the application of colour image compression. The beauty of the SVD within its digital applications is that it provides a robust method of storing large images as smaller, more manageable ones. This is accomplished by reproducing the original image with each succeeding non-zero singular value. Furthermore, to reduce storage size even further, one may approximate a good enough image using even fewer singular values.
Similar to the SVD of a gray image, the SVD of a colour image Q can be decomposed into the summation of vector outer products
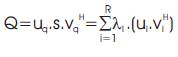
where ui and vi are the column vectors of matrix U and V , respectively and H represents the quaternion Hermitian transpose operator, or conjugate–transposition operator, λi’s are the diagonal terms of real matrix S (i.e. the singular values), and R is the rank of Q. Every product ui . viH an eigen-image. Hence, the colour image ƒ(x,y) represented by Q can be considered as the linear combination of R colour eigen-images. Similar to the complex matrix, the preceding eigen-images represent the low-frequency components of the original image, and the later ones represent the high-frequency components. Figures 2-4 illustrate first, second, and fourth colour eigen- images of Mandrill, Lena and Flower colour images.

Figure 2. Selected Eigen-images Of Mandrill Colour Image (a) Original image of size 330 x 330 (b) u1 v1H ( c ) u2 v2H (d) u4 v4H

Figure 3. Selected Eigen-images of Lena Colour Image H H H (a) Original image of size 512x512. (b)u1 v1H ( c ) u2 v2H (d) u4 v4H

Figure 4. Selected Eigen-images of Flower Colour Image (a) Original Image of size 330x330 b)u1 v1H ( c ) u2 v2H (d) u4 v4H
The singular values distribution of Mandrill and Lena colour images are shown in Figure 5 (a & b). The QSVD distribution of these images shows that these images are full rank images (none of the 512 singular values for Lena image and 330 singular values for Mandrill image equals zero). The image is full rank means that all the singular images are necessary to rebuild the original exactly. The same phenomenon as in the conventional complex case, the singular values decay very fast. Hence, an approximate representation of a colour image can be obtained by summing the first K eigen-images.
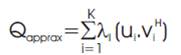
where K≤R. The real part of Qapprox is small and will decrease to zero when K increases to R and one colour image has only three components, so the real part of Qapprox will be discarded. In general, even small K can provide a good approximation of the original colour image. Consequently, the storage requirements for this colour image drop from 3xNxN to K(2x4N+1) (including K real singular values; 2K x N quaternion vectors).
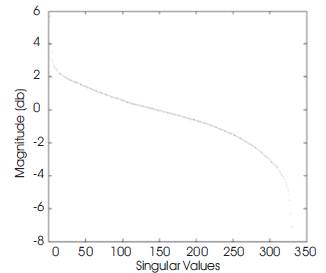
Figure 5. Singular Values of Two Colour Images. (a) Mandrill
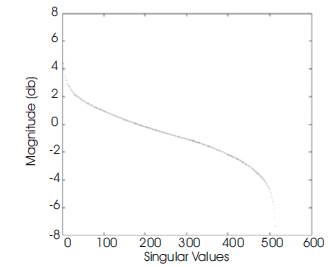
Figure 5. Singular Values of Two Colour Images. (b) Lena
In this section, they present results of application of the QSVD for compression on the Mandrill, Lena and Flower colour images. Figure 6 illustrates four estimated images of the Mandrill colour image based on QPCA. In Figure 6 (b)-(e), the images are reconstructed with K=3, 20, 50, 255(the perfect reconstruction). Usually, when the image has more high frequency components, greater K is necessary to have a good approximation. On the other hand, for images containing mostly low frequency components, the performance of this reconstruction is good with small K. By comparing the two approximations in Figure 6 (d) and (e), it is clear that a good enough representation may be found with far fewer singular values.This substantially reduces the amount of information necessary to store the exact image. This is a real life example of the power and efficiency of the singular value decomposition. Let us look at the numbers involved. Because the original image before the SVD was 330x330, it requires 330x 330x3=326700 entries for storage. The image produced by the first 20 singular values requires only 20x330x4 entries; the image with the first 50 requires 50x330x4. This drastically reduces the information necessary to 8.08% and 20.2% of the original image, respectively. Figure 7 illustrates four estimated images of the Lena colour image based on QPCA. In Figure 7 (b)-(e), the images are reconstructed with K=5, 20, 50, 300 (the perfect reconstruction). Table 1 shows the compression ratios obtained with different values of K.
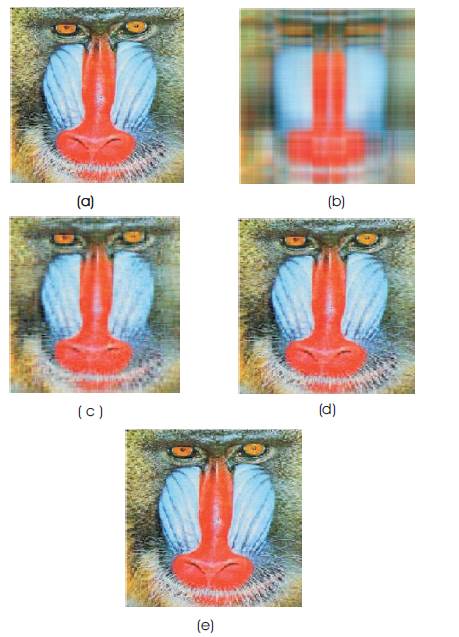
Figure 6. QPCA Based Image Compression. (a) Original Mandrill Colour Image Original Image of size 330x330 (b)–(e) are the reconstructed images with K=3, 20, 50, 255. Note that (e) is the Perfect Reconstruction of the Original Image.

Figure 7. QPCA Based Image Compression. (a) Original Lena Colour Image Original Image of size 512x512 (b)–(e) are the reconstructed images with K=5, 20, 50, 300. Note that (e) is the Perfect Reconstruction of the Original Image.
In order to quantify the way information is distributed into the singular values and to analyze the performance of this estimation, the PSNR of the estimated colour images for K=10,30,50,70,90,110 and for three colour images, “Mandrill, Lena and Flower”, are given in Table 2. The colour image Lena has many high frequency components, so the performance is the worst among these 3 images. The Flower colour image has less high frequency components, so the performance is the best.
Figure 8 shows the plot of the PSNR for different values of K and reconstructed images of Mandrill image. The PSNR is calculated using the formula
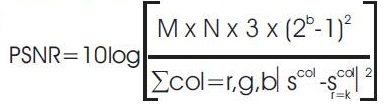
where K corresponds to the number of singular images used to reconstruct the image, M x N is the size of the image and for an 8-bit image, b=8. The image reconstructed with 10 singular image is at PSNR= 25.3812db while the one reconstructed with 30 images is at PSNR=28.9271 db. Then from 30 to 110 singular images, the PSNR increases to PSNR=39.2051 db. Looking at reconstructed images, the one reconstructed with 110 images looks quite good, even though the PSNR is only 39.2051 db. Comparing the PSNR and singular values plots, one can see that they look like inverse of each other. This allows to interpret the singular values obtained by QSVD of a colour image as a distribution of structural and colour energy in the image.
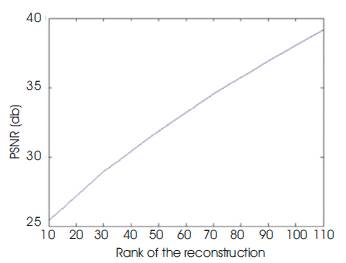
Figure 8. PSNR Values of the Reconstructed Images of the Mandrill Colour Image With QSVD Compression.
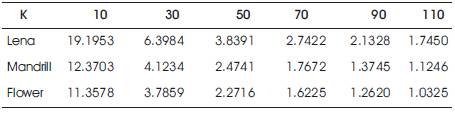
Table 1. Compression Ratios Obtained With Different K Eigen- Images
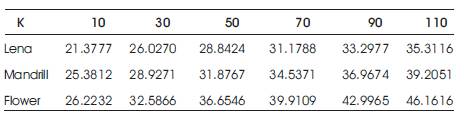
Table 2. PSNR of the Approximated Colour Images, Lena, Mandrill and Flower
The authors have proposed a new approach for colour image compression based on quaternion matrix algebra and quaternion singular value decomposition. The decomposition of a colour image is possible using QSVD and leads to the expression of the original colour image into a sum of colour eigen–images. Structural and colour information is encoded in singular images and the progressive reconstruction of the original image with its singular elements is closely related to the PSNR. Future work will concern application of QSVD for colour image de-noising and watermarking.