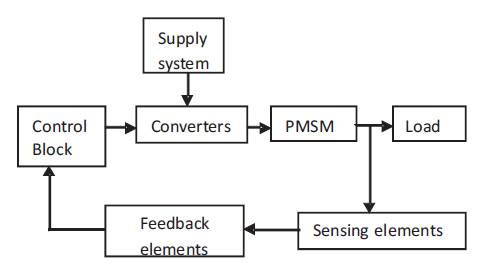
Figure 1. Block Diagram of PMSM Drive
Permanent Magnet Synchronous Motor (PMSM) drives are being used increasingly in a wide range of applications, such as machine tools, robotics, aerospace generators, actuators and electric vehicles. It is extensively used in industrial applications due to it's advantageous features such as high efficiency, high torque to inertia ratio, low noise and robustness. In advanced motor control system, an accurate knowledge of motor parameters are essential in order to achieve better performance. Machine parameters are classified into electrical parameters such as resistances of windings and d, q axes inductances of both stator and rotor and mechanical parameters such as angular position, speed, moment of inertia and viscous friction coefficient. Various types of parameter estimation methods for PMSM are available in the literature such as back e.m.f. based method, signal injection based method, state observer based method, Model Reference Adaptive System (MRAS) based method etc. This paper presents a review of all these methods used to estimate the parameters of a Permanent Magnet Synchronous Motor.
Electrical machine which converts electrical energy into mechanical energy and vice versa is the work space in the drive system. Drive systems are widely used in applications such as pumps, fans, robotics, textile mills, elevators, electric vehicles etc [38]. More than 85% of drive systems are induction motors at present but Permanent Magnet Synchronous Motors (PMSM) can replace them. As they are more efficient, less maintenance cost and compact in size which in turn reduces the replacement cost [1]. The stator current of an Induction Motor (IM) contains magnetizing as well as torque producing components, whereas in PMSM due to the usage of permanent magnets on rotor, magnetizing current component is absent, therefore the stator current provides only torque producing component [2]. Hence for the same output, the PMSM will operate at a higher power factor (because of the absence of magnetizing current) and will be more efficient than the IM. On the other hand, the conventional wound-rotor synchronous motor must have dc excitation to the rotor, which is often supplied by brushes and slip rings. This implies regular brush maintenance and rotor losses, which reduces life of the machine.
The PMSM drive can be implemented by two modes such as (i) Open loop control (ii) Closed loop control. The implementation block diagram of PMSM drive is shown in Figure 1.

Figure 1. Block Diagram of PMSM Drive
 (a) Linear model
(a) Linear model (b) Non-linear model
(b) Non-linear model (a) Scalar control (open
loop control)
(a) Scalar control (open
loop control) (b) Vector control
(closed loop control)
(b) Vector control
(closed loop control) (a) Rectifiers (1-phase
& 3-phase)
(a) Rectifiers (1-phase
& 3-phase) (b) Inverters (1-phase
& 3-phase)
(b) Inverters (1-phase
& 3-phase) The feedback elements
are treated as rotor rotating
angle, speed, torque and currents.
The feedback elements
are treated as rotor rotating
angle, speed, torque and currents. (a) Using mechanical
sensors
(a) Using mechanical
sensors (b) Using different
observers
(b) Using different
observersThe design of control system for a high performance drive requires a mathematical model of the machine. Mathematical model is usually derived from physical principles [39]. The dynamics of a sinusoidal PMAC motor can be described by a set of differential equations relating voltages, currents (fluxes), speed and torque. The equations are modelled in d-q axes variables in the rotor reference frame using Park's transformation.
The sinusoidal PMAC motor are similar to the salient pole motors, except that there is no field winding and the field is provided instead by mounting permanent magnets in the rotor. The excitation voltage cannot be varied. The elimination of field coil, dc supply and slip rings reduces the motor loss and complexity. These motors, also known as brushless motors, which finds applications in robots and machine tools etc. [1].
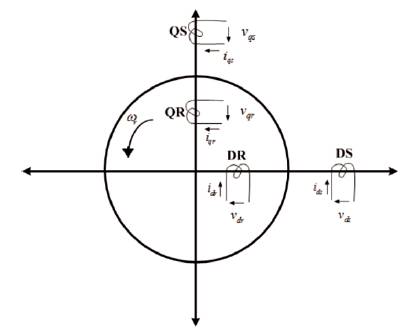
Figure 2. Permanent Magnet Synchronous Machine
The schematic diagram of PMSM with damper windings is shown in Figure 2. The model of PMSM with damper winding has been developed on rotor reference frame [2] using the following assumptions:
The voltage equations for the permanent magnet motor in rotor reference frame are [40] as follows,
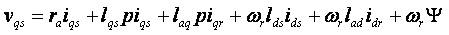
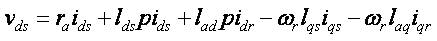
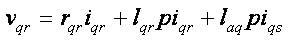
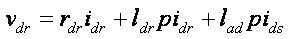
where, Ψ = lad ifr = air gap flux linkage
Equation (1) can be rewritten as,
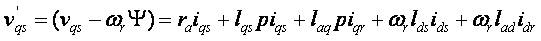
where all voltages (v) currents (i) are refer to the rotor reference frame. The subscripts qs, ds, qr and dr correspond to q and d axis quantities for the stator(s) and rotor(r) in all combinations, ra denotes the armature resistance, lqs denotes quadrature axis inductance, lds denotes direct axis inductance etc.
Equations (1) to (5) can be represented in matrix form as given below,
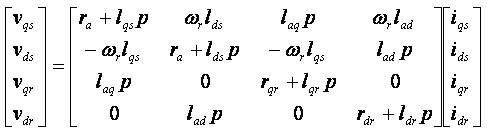
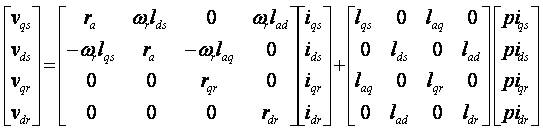
In the abbreviated form, the matrix can be written as,
[Voltage column matrix] = [impedance matrix] × [current column matrix]
i.e. [V] = [Z] × [I] and it will be modified as,
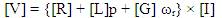
where [R] is the resistance matrix, [L] is the inductance matrix and [G] is the torque matrix or motional inductance matrix or rotational inductance matrix.
The electromagnetic torque [40] is an important output variable, which gives mechanical parameters of the machines rotor position and speed.
The voltage equations can be written as follows,
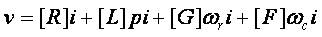
where R matrix consists of resistive elements, L matrix consists of derivative inductive elements, G matrix has coefficients of electrical rotor speed ωr , F is the frame matrix in terms of coefficient of reference frame speed, ωc.
Now pre-multiplying the above equation by the transpose of the current vector, gives the instantaneous input power as,
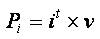
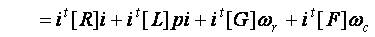
From the fundamentals, it is known as air gap power has to be associated with rotor speed. The air gap power is the product of the mechanical rotor speed and electrical magnetic torque.
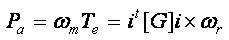
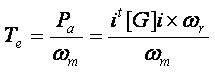
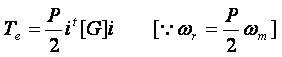
The factor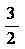 is introduced
into the equation from the
power equivalence condition between the 3 phase and
the 2 phase [4].
is introduced
into the equation from the
power equivalence condition between the 3 phase and
the 2 phase [4].

The G matrix from above equation (7) can be obtained as;

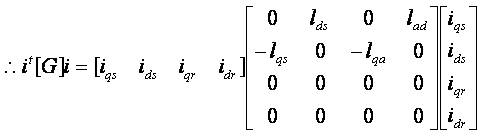
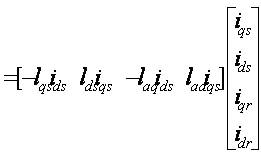

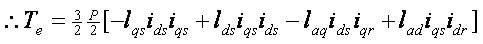
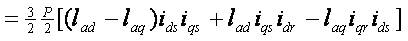
and the load torque becomes
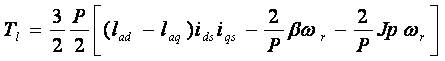
Hence by using system and torque equations PMSM motor can be modeled.
In advanced motor control system, an accurate knowledge of motor parameters is essential in order to achieve good dynamic performance. Meanwhile, control techniques such as Field Oriented Control (FOC) and Direct Torque Control (DTC) for controlling PMSM are also still developing and improving. In FOC method, the design of the current loop controller is based on the stator resistance and stator inductance. In addition, parameters of speed loop and position loop controller are also influenced by the current loop control parameters. In DTC method, electromagnetic torque and stator flux are used as control variables to directly control the torque and flux. So it is necessary to estimate the parameters of the PMSM accurately to achieve good dynamic performance of the drive system.
In order to achieve an accurate and good dynamic performance of the drive system, machine parameters need to estimate accurately. Some of these parameters, such as stator resistance are given by constructors, but it varies in different operating conditions. The purpose of this paper is to present an efficient dynamical identification method to estimate parameters of a PMSM. Using the below mentioned methods, one can determine the parameters of PMSM during different operating conditions. The machine parameters can be determined analytically or by the analysis of magnetic field during the machine operation [3]. Estimation is the comparison of known parameters with experimental values. Estimation of physical parameters like flux linkages are difficult because the machine operates into deep saturation. Mainly machine parameters can be classified into two types.
Winding resistance and inductance of stator and rotor in both d-q axes.
Angular velocity, rotor position in mechanical degrees, moment of inertia and viscous friction coefficient.
PMSM is frequently used in the industry due to its high efficiency and quick mechanical dynamics [5]. To design high performance control systems, it is important to have an accurate knowledge of the machine parameters. The data sheet containing the motor parameters that come out from the manufacturer is not always available, and when a new PMSM is to be installed in an application, it is desirable to identify the parameters with parameter identification automatically. This is also more time efficient compared to manually changing the parameter values. Even when the data sheet is available, it does not usually take care about some parameters that tend to vary during different operating conditions. Classical motor control techniques such as vector control require a position sensor to control the PMSM, and in such case, the parameter information from the data sheet is normally sufficient. Since a sensor brings high cost and sometimes low reliability, it is desirable to remove the sensor, which will require the more advanced control techniques. Many position sensor-less control methods are reliable on an accurate motor model and by introducing an on-line parameter identification in such drive systems, it is possible to improve the control performance [3].
Techniques that determine motor parameters during a standstill or rotation without any load are called "off-line parameter identification methods". The off-line methods can further be categorized as self-commission and commission methods. In self-commission, all required motor parameters suitable for control are determined without any previous knowledge about the parameter values. In commission, some previous information about the parameter values are required.
The techniques that adapt the motor parameters during the drive operations are called "on-line parameter identification methods". Many on-line identification algorithms with different nature have been proposed in earlier literature and they can be categorized into various groups.
A number of estimation techniques have been developed to achieve speed and position of sensorless PMSM drives. Most of these suffer from the variation of motor parameters such as stator resistance, inductance and torque constant. The conventional linear estimators are not adaptive to the variations of the operating conditions in a non-linear system. The sliding mode control technique has shown promising results in order to estimate the parameters of a non-linear system. In this technique, the robustness of the motor parameter estimation can be guaranteed. This can be applicable for both linear time invariant and non-linear systems.
In this method, position of rotor and speed of PMSM is easily estimated. This technique can be generalized to other motor drives and motion control systems. It is observed that the observer gains have great influence on the performance of the observer and it is mechanically unreliable.
The stator resistance method is an online method for parameter estimation of PMSM based on the extended EMF model. This method can be applicable for all types of synchronous machines. The stator resistance is sensitive to the temperature and frequency variations.
The rotor resistance estimation method is based on the motor model that takes magnetic saturation into account. In this method, mechanical as well as electrical parameters such as rotor resistance and angular position of rotor can be estimated. This method can be applicable for all types of SM, PMSM and SRM. It requires continues input and output operating data.
The standstill method is used for identifying the linear parameters, operational impedances and the time constant of a salient pole PMSM. The parameters of PMSM are identified from standstill test data. To conduct the standstill tests, different test signals like excitation voltages at standstill condition and the following currents in different windings of the machine must be known. This test also provides complete data about direct and quadrature axes parameters.
This test can be done in either on-site or at industry and it posses low possibility of risk to the machine being tested. But it requires more measuring circuit and hence expensive.
This is an online method to estimate parameters of large size PMSM. In this method, armature circuit parameters of machine using real time operating data are estimated. This method can be easily applied when the operating data, synthetic input and output data are available. It is an alternative method for approximation of functions. The problem of system identification using orthogonal series expansion includes linear time invariant, lumped and distributed systems and non-linear systems. The parameter estimation algorithm, developed originally to detect the field turns are to be shorted for PMSM under steady state.
The advantage of this method is the detection of turn-to-turn shorts of fielding winding of a synchronous machine. So the accuracy of this method is high. But, it requires time to time operating data of the system.
The Kalman's filter method can be used to estimate the equivalent circuit parameters like resistances and inductances. It can be applicable only for linear models of the machine, and requires continues operating data for estimation. This method is used to estimate the stator winding resistance, rotor flux linkages of permanent magnet and temperature rise in stator winding. Magnet saturation causes temporary changes to the machine inductances according to the operating point of the machine.
Kalman's filter is an estimator and can be used to track a dynamic process of the machine. This approach requires an assumption of the model of process being tracked. This method estimates the machine parameters with a reasonable accuracy when system connected to a large disturbance i.e. grid or source. This method is more sensitive to sampling time.
The usage of high performance PMSM drive applications are increasing day-by-day. PMSM with accurate parameters are significant for precise control system design. This method proposes an intelligent model parameter identification using Practical Swarm Optimization (PSO) approach. PSO is a versatile and efficient tool for optimization. To design advanced controller for PMSM, it is very important to obtain an appropriate model of the motor. In this method, stator resistance and load torque disturbance of PMSM are identified. PSO is a population based stochastic search algorithm, which has been widely used to solve a broad range of optimization problems. It is also applicable for other types of electrical motors.
PSO algorithm is capable of tracking time varying parameters with good accuracy. But PSO based identification method is not applicable for complicated non-linear models.
In this method, back e.m.f. is used to estimate the rotor speed. This method offers satisfactory performance at higher speeds. However, at zero or very low speed, the back e.m.f. becomes negligible. This makes the speed estimation at lower speed very difficult. Also, the method is highly sensitive to machine parameters.
Sometimes the phase inductance varies for different rotor positions due to the saliency present in the rotor side. To extract the position from inductance profile, a high frequency voltage signal is fed to motor phases. This method is reliable at zero speed.
However, the accuracy of this method is highly influenced by the geometry of the rotor, so it is not suitable for surface mounted PMSM. The main drawback of this method is the adverse effect of injecting signal on motor dynamics and extra hardware requirement. This method is used for sensorless schemes at standstill.
In this method, the parameter can also be treated as the state and which can be estimated along with the rotor speed. To overcome the chattering phenomenon, a low pass filter is used, which increases cost of the drive system.
The computational complexity, parameter sensitivity and the need of initial conditions degrade the superiority of this method. It offers more stability.
MRAS based method is used for online identification of the PMSM parameters. MRAS computes a desired state using two different models such as reference model and adjustable model as shown in Figure 3. The error between the models is used to estimate an unknown parameter. A condition to form the MRAS is that, the adjustable model should only depend on the unknown parameter. Here, the reference model is independent of the rotor speed, whereas the adjustable model is dependent on the same.
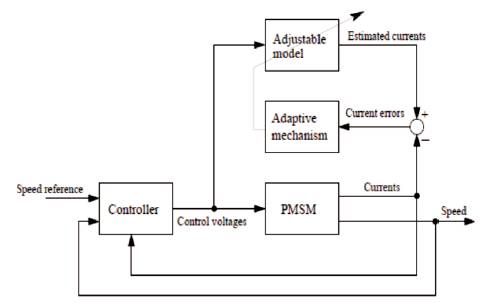
Figure 3. Block Diagram for MRAS
The error signal is fed to the adaptation mechanism. The output of the adaptation mechanism is the estimated quantity, which is used for the tuning in adjustable model and also for feedback. It is a simple method and requires less computation, but it does not work well with low torque and at standstill conditions.
It is an online parameter identification method used to estimate the parameters of both surface and interior permanent magnet synchronous motors. In this method, to identify the unknown parameters of the motor, mathematical model using known values (such as voltages and currents) is used. The mathematical model can be constructed on a stationary or rotating reference frame. This method gives better results in rotating reference frame because the model coefficients can be assumed to be almost constant.
As this method does not use rotor position or velocity to identify motor parameters, the identified parameters are not affected by position estimation error under sensorless control. But it requires more data for every estimation and more non-linear equations are to be solved.
In this method, by measuring machine input voltages, output currents, speed, and internal parameters of the machine can be estimated. In the identification stage, the model excitation signals are the current values and speed of the machine and the response signals are the input voltages. After getting the model, the output currents and electrical torque of the machine can be calculated, by knowing the input voltages and the speed of the machine.
If the model based current estimations are reliable enough to replace the current sensor information, then the machine can be controlled and torque can be estimated without having current sensors. It is more complex for the system having non-linear equations and hence it requires more calculations.
The open-loop performance characteristics of PMSM for a step change in speed corresponding to a frequency of fr =40Hz to 50Hz at a constant load torque of TI =0.6 N-m using MATLAM/SIMULINK are shown in Figures 4-9. The stator winding currents are shown in Figures 4 and 5, where as the rotor or damping winding currents are shown in Figures 6 and 7. From the results it is clear that, the system maintains stability in the aforesaid frequency range. For the frequency less than fr =39Hz, the system becomes unstable. One can estimate the parameters of the PMSM under stable condition only. Figures 8 and 9 show the speed of the PMSM without and with inverter respectively. Form the figures, it is clear that the inverter fed motor will have reduced oscillations when compared to those without the inverter fed motor under transient condition.
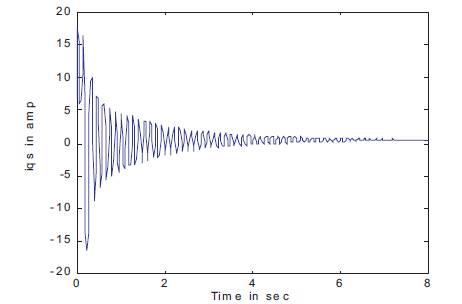
Figure 4. iqs Current Waveform
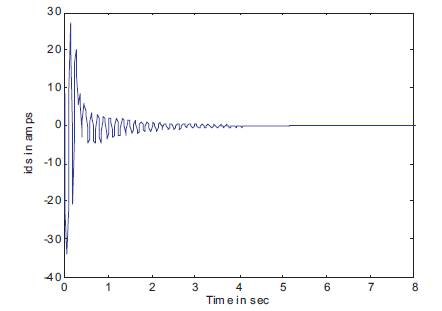
Figure 5. ids Current Waveform
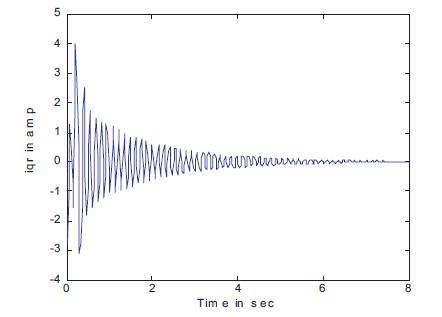
Figure 6. iqr Current Waveform

Figure 7. idr Current Waveform
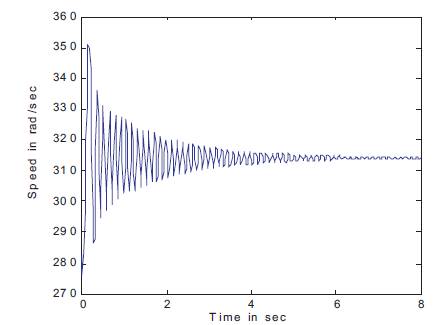
Figure 8. Speed Waveform without Inverter

Figure 9. Speed Waveform with Inverter
In this paper, an investigation of parameter estimation methods of PMSM have been discussed. PMSM has been modelled in rotor reference frame by using Kron's primitive machine. To design high performance control systems, it is important to have accurate knowledge of the machine parameters. This paper provides the basic information about parameter estimation methods and its merits as well as demerits. These methods can be suited for both sensor and sensorless machine. The electrical parameters are estimated by off-line as well as on-line techniques but mechanical parameters are estimated by on-line methods only. The open loop speed and performance characteristics of PMSM are also presented.