(1)
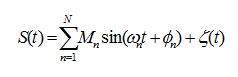
Estimation of power system parameter plays an important role in the modern power system. In this paper, estimation of harmonics components in a power system synthetic signal is done by an improved estimation technique called as ADALINE. This neural estimator basically uses an adaptive interpreted linear neuron. Learning parameter is adjusted to keep the difference between the Real and Expected values to satisfy the difference that arises due to error equation. Tracking of the fourier co-efficent of the proposed signal, which also constitutes a noise, and DC decaying component can be done easily and accurately using the proposed algorithm. To verify the effectiveness of the proposed algorithm, estimation of amplitude as well as Phase of fundamental and harmonics is carried out. The simulation results obtained are encouraging to work more on the estimation of signals.
Power quality in power system increases the attention of many researchers working in the area of power quality. Use of power semiconductor devices in generation, transmission, and distribution sectors result in harmonics in the modern power system, which deteriorates the power quality. This degradation of power quality affects the operation and control of the power system, unnecessary tripping, more losses in the transformer core, etc. (Mori et al., 1992; Al-Feilat et al., 1994; Ray et al., 2015). Several remedies (Ray et al., 2015; Dash et al., 1996), such as dynamic voltage regulator, noise fi l ter, con s tan t vol tage tran s former, i s ol ati on transformer, transient voltage surge suppressor, static var compensators, and harmonics filters (Ray, et al., 2015) have been developed to improve the performance and efficiency of the power system.
Proper and accurate estimation of amplitude and phase of harmonics components is essential to design the harmonics filter so that implementation of control techniques is easily adopted. Various control techniques, such as proportional integral, indirect current control, synchronous detection, partial feedback linearization, neural network, and fuzzy logic controller (Al-Feilat et al., 1994) were discussed. If proper filtration technique is not implemented then inter harmonics and sub harmonics originates and entirely damages the power system (Al-Feilat et al., 1994; Ray et al., 2015). To provide the quality of the deliver power, it is necessary to know the harmonic parameter such as magnitude and phase. Many algorithms are available to evaluate the harmonics of the power system (Dash et al., 1996; Lobos et al., 2001; Liu 1998; Dash & Sharaf, 1998; Watson & Arrillaga 2003; Mishra, 2005; Kumar et al., 2006; Qidwai & Bettayeb, 1998; Bettayeb & Qidwai, 2003; Haykin, 2008; Ljung, 1999). Many well-known techniques, such as least square error techniques, (Kennedy et al., 2003; Ray & Subudhi, 2015), Newton method, Fast fourier transform (Ray et al., 2015), and wavelet transform have been used for power system harmonic and frequency estimation.
This work develops a modified adaptive linear neural network technique followed by Dash and Sharaf (1998) called ADALINE. ADALINE structure is used to estimate the fundamental and harmonics components of signal. The structure of the ADALINE is a mixture of various sequences, such as input, output, and an expected response along with adjustable parameters which can be updated by weight vector (Puhan et al., 2015; Panda et al., 2014). After the harmonic components are estimated, the signal is passed through the filter and power quality of the system is improved.
Negative effects of harmonic currents and voltages are signal interference, overvoltages, data loss (Dash et al, 1996; Reddy et al., 2015; Sekaran, 2006; Yadav & Singh, 2017), and circuit breaker failure, as well as equipment heating, malfunction and damage. Harmonics are responsible for introduction of noise on telephone and data transmission lines, huge increases in computer data loss, excessive heating in transformers and capacitors resulting in shortened life or failure. Rotor heating and pulsating output torque caused by harmonics can result in excessive motor heating and inefficiency.
Let us assume the voltage or current waveforms of the known fundamental angular frequency w as the sum of harmonics of unknown magnitudes and phases. The general form of the waveform is,
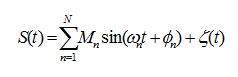
where,
N is the number of harmonics. ωn = n2πf0 ; f0 is the fundamental frequency; ς(t) is the additive noise. The discrete time version of equation (1) can be represented as,
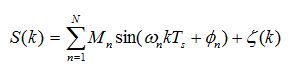
where, Ts is sampling period.
The non-linearity that arises in the model is used to phase the sinusoids. From the discrete signal of equation (2), the amplitudes and phases of the fundamental and all the harmonics components are estimated.
The estimation of harmonics parameter such as amplitude and phase can be carried out as follows. Now for this purpose, equation (2) can be rearranged into equation (3)
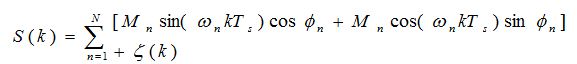
The formulation of the above equation is utilized to find the estimation of fundamental and harmonics magnitude and phase angle error.
Figure 1 shows the block diagrammatic representation of ADALINE. Product of input signal and weight of the ADALINE gives the estimated output and is compared with the desired output. The error obtained is minimized by updating the weight of the ADALINE.
The input to the ADALINE is,
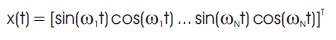
The weight vector of the ADALINE is,
Figure 1. Developed ADALINE Model
The optimized output of the unknown parameter using BFO algorithm is taken as the initial values of the weight vector of ADALINE and it is updated using a modified Widrow-Hoff delta rule as
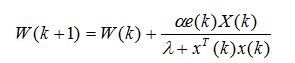
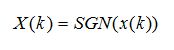
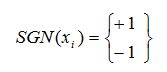
+ 1 if xi > 0
-1 if xi < 0
i = 1, 2, ...., 2N + 2
0 < α < 2
The learning parameter α can be adapted using the following expression,
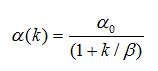
where α0 is the initial learning rate and β is decaying rate constant. λ is a small quantity and it is usually chosen to make
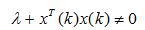
The value of λ is taken as 0.01.
Once the updation steps are completed for the weight vector, which is one of the important parameters to be learned, the other parameters, such as amplitude of harmonics components, phase angle of the harmonics component, and the fundamental signal are derived as followed by the equations (11) and (12).
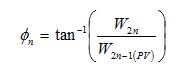
The performance evaluation of the developed algorithm is carried out by generating a synthetic signal using MATLAB. The synthetic signal is a combination of fundamental and various harmonics signals, such as 3rd , 5th , 7th , and noise. The developed signal is industrial in nature.
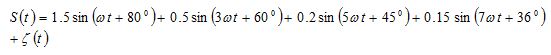
A random noise of ς(t) = 0.01 rand with normal distribution zero mean and unity variance.
Figure 9 represents the estimation of phase of 7th harmonics component estimation and actual performance of the signal is shown in Figure 2 and the estimation of the amplitude and phase of the 3rd , 5th and 7th harmonics component are shown in Figures 3 to 9, using the developed ADALINE algorithm.
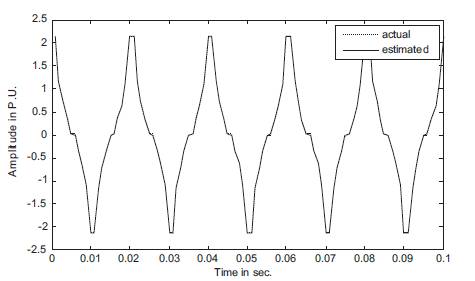
Figure 2. Plot of Estimation and Actual Signal
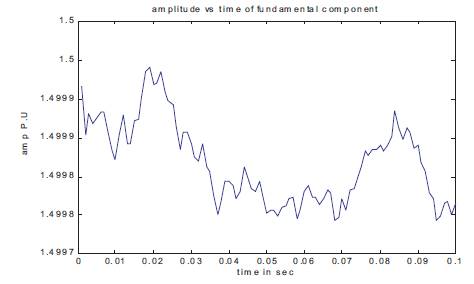
Figure 3. Estimation of Fundamental Amplitude of Signal
Figure 4. Estimation of 3rd Harmonic Amplitude of Signal
Figure 5. Estimation of 5th Harmonic Amplitude of Signal
Figure 6. Estimation of 7th Harmonic Amplitude of Signal
Figure 7. Estimation of Fundamental Phase of Signal
Figure 8. Estimation of 3rd Harmonic Phase of Signal
Figure 9. Estimation of 7th Harmonic Phase of Signal
Figures clearly state that the estimated magnitude and phase of the different types of harmonic component matches with the mentioned value in the signals (equation 1).
Figure 10 shows the segregation of estimation of fundamental and all the harmonics of that signal using ADALINE. From Figure 10, it is seen that highly accurate estimation is obtained in each case of estimation.
Figure 10. Segregation of Estimation of all Components
Table 1 shows the accuracy of the estimated values compared to the actual values in all cases of estimation. th Maximum deviation in amplitude of 3.1% occurs at 7 harmonic estimation and maximum deviation in phase of 0 t h 1.21 occurs at 7 harmonics estimation. The computational time required for the estimation is 0.336 seconds.
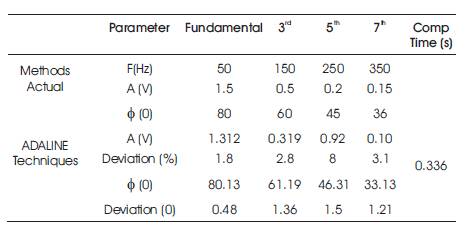
Table 1. Comparison of Estimated vs. Actual Value using ADALINE
This paper presents ADALINE for accurate estimation of amplitudes and phases of the harmonics contained in a voltage or current waveform for power quality monitoring. Various simulations are carried out and the results obtained are analysed with respect to the estimation accuracy, speed of convergence, and settling time and it is observed that the proposed algorithm gives very encouraging results, which can be used to estimate the inter-harmonics and also the sub-harmonics.