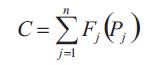
Particle swarm optimization has emerged as a useful optimization tool for handling nonlinear programming problems. Various modifications to the basic method have been proposed with a view to enhance speed and robustness and these have been applied successfully on some benchmark mathematical problems. But few applications have been reported on real-world problems such as economic dispatch (ED) with non smooth cost functions. To show improved particle swarm optimization (IPSO) in efficiency and effectiveness, the proposed IPSO is applied to test the economic dispatch problems, with non-smooth cost functions considering valve-point effects and multi-fuel problems. The results of the IPSO are compared with the results of conventional numerical methods, evolutionary programming approaches and genetic algorithm.
Finally the convergence characteristics of improved particle swarm optimization (IPSO) are compared with modified particle swarm optimization results (MPSO).
Recently, ECONOMIC dispatch (ED) is an important optimization task in power system operation for allocating generation among the committed units such that the constraints imposed are satisfied and the energy requirements interms of British thermal units per hour (Btu/h) or dollar per hour ($/h) are minimized. Improvements in scheduling the unit outputs can lead to significant cost savings. Most of the power system optimization problems including economic dispatch (ED) have complex and non-linear characteristics with heavy equality and in equality constraints. Recently, as an alternative to the conventional mathematical approaches, the heuristic optimization techniques such as Genetic algorithm, simulated annealing and recently introduced particle swarm optimization (PSO) are considered as realistic and powerful solution schemes to obtain the global or quasi global optimums in power system optimization problems[1].
The particle swarm algorithm is a method for optimizing hard numerical functions based on a metaphor of human social interaction (Eberhart, Simpson, and Dobbins, 1996; Kennedy,1997) [2] . Individual s represented as multidimensional points interact with one another and converge on optimal regions of the problem space. While originally developed as a simulation of social behavior, the algorithm has become accepted as a computational intelligence technique related to evolutionary algorithms. The main advantages of the PSO algorithm are summarized as simple concept, easy implementation, robustness to control parameters and computational efficiency when compared with mathematical algorithm and other heuristic optimization techniques.
The practical ED problems with valve-point and multi-fuel effects are represented as a non-smooth optimization problem with equality and inequality constraints and this makes the problem of finding the global optimum difficult. To solve this problem, many salient methods have been proposed such as a mathematical approach, dynamic programming, evolutionary programming [3], and genetic algorithm[4] .
In this paper, an alternative approach is proposed to the non-smooth ED problem using a improved particle swarm optimization (IPSO), which focuses on the treatment of the equality and inequality constraints when modifying each individual's search and introduces a constriction factor in the velocity update equation while limiting the maximum value of velocity (Vmax ) to position maximum(Xmax ). The equality constraint (i.e., the supply/demand balance) is easily satisfied by specifying a variable (i.e., a generator output) at random in each iteration as a slag generator whose value is determined by the difference between the total system demand and the total generation excluding the slag generator.
The ED problem is to find the optimal combination of power generations that minimizes the total generation cost while satisfying an equality constraint and inequality constraints.
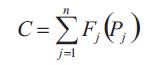

Where PD is the total system demand.
The generation output of each unit should be between its minimum and maximum limits. That is, the following inequality constraint for each generator should be satisfied.
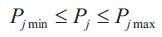
In reality, the objective function of an ED problem has non differentiable points according to valve-point effects and change of fuels; therefore, the objective function should be composed of a set of non-smooth cost functions. In this paper, two cases of non-smooth cost functions are considered. One is the case with the valve-point loading problem and the other is the case with the multiple fuel problems.
For large steam turbine generators, the input-output characteristics is shown in Figure1. Large steam turbine generators will have a number of steam admission valves that are opened in sequence to obtain ever-increasing output of the unit. As the unit loading increases, there by the input to the unit increases and the incremental heat rate decreases between the opening points for any two valves. However, when a valve is first opened, the throttling losses increase rapidly and the incremental heat rate rises suddenly. This gives rise to the discontinuous type of characteristics in order to schedule steam unit, although it is usually not done. This type of input-output characteristics is non-convex; hence, optimization technique that requires convex characteristics may not be used with impunity.
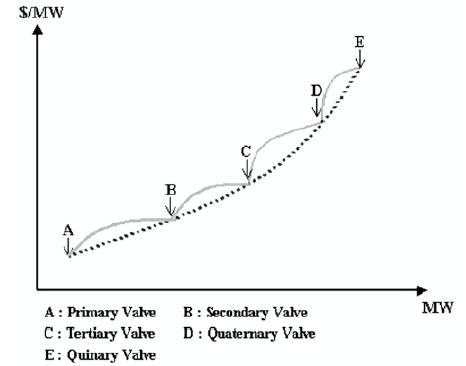
Figure 1. Example of cost function with 5 valves
In valve point loading problem, the objective function is generally described as superposition of sinusoidal functions and quadratic function given in eqn (4).
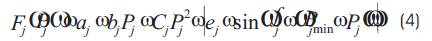
Generally, a piecewise quadratic function is used to represent the input-output curve of a generator with multiple fuels shown in Figure 2. The piecewise quadratic function is described as eqn (5).
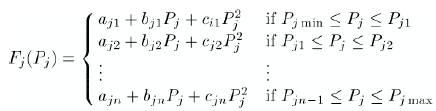

Figure 2. Piecewise quadratic and incremental cost functions of a generator.
PSO algorithm is developed by simulating human social behavior and individuals of a swarm. Particle swarm optimization has roots in two main component methodologies. Perhaps more obvious are its ties to artificial life (A-life) in general, and to bird flocking, fish schooling and swarming theory in particular. It has been noticed that members within a group seem to share information among them, a fact that leads to increased efficiency of the group. The PSO algorithm searches in parallel using a group of individuals similar to other AIbased heuristic optimization techniques.
PSO algorithm searches in parallel using number of individuals. An individual in a swarm approaches to the optimum or a quasi optimum through its present velocity, previous experience, and the experience of its neighbors. In a physical -dimensional search space, the position and velocity of individual are represented as the vectors Xi=(xi1, xi2 ……..,xin ) and Vi =(vi1 ,vi2 ,…….,vin ) , respectively, in the PSO algorithm.
Let 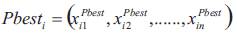 and
and 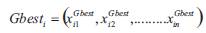 respectively, be the best position of individual and its neighbors' best position so far. Using the information, the updated velocity of individual is modified under the following equation in the PSO algorithm.
respectively, be the best position of individual and its neighbors' best position so far. Using the information, the updated velocity of individual is modified under the following equation in the PSO algorithm.
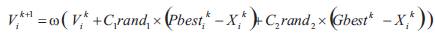
Where
Vik Velocity of individual i at iteration k
ω constriction factor
C1, C2 Weight factors
rand1, rand2 random numbers between [0 1]
Xik Position of individual i at iteration k
Pbestik best position of individual i until iteration k
Gbestk best position of the group until iteration k
Each individual moves from the current position to the next one by the modified velocity in eqn(6) using eqn (7).

The search mechanism of the PSO using the modified velocity and position of individual based on eqns (6) and (7) is illustrated in Figure 3.
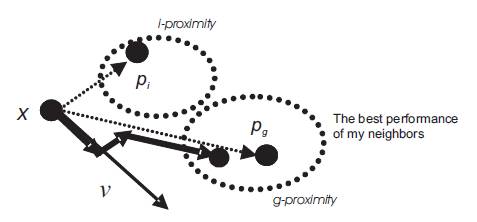
Figure 3. The Search Mechanism of the Particle Swarm Optimization
In this section, a new approach to implement the PSO algorithm will be described in solving the ED problems. The process of the modified PSO algorithm can be summarized as follows:
Step 1) Initialization of a group at random while satisfying constraints.
Step 2) Velocity and position updates while satisfying constraints.
Step 3) Update of Pbest and Gbest.
Step 4) Activation of space reduction strategy.
Step 5) Go to Step 2 until satisfying stopping criteria.
In the initialization process, a set of individuals is created at random. In this paper, the structure of an individual for ED problem is composed of a set of elements (i.e., generation outputs). Therefore, individual's position at iteration 0 can be represented as the vector of (i.e., Zi0 =(Pi10 ,.....,Pin0 )where 'n' is the number of generators. The velocity individual i (i.e.,Vi0 =(ωi10,......ωin0)) corresponds to i i1 in the generation update quantity covering all generators. The elements of position and velocity have the same dimension, i.e., MW in this case. The following procedure is suggested for any individual in a group
Step 1) Set j=1.
Step 2) Select an element (i.e., generator) of an individual at random.
Step 3) Create the value of the element (i.e., generation output) at random satisfying its inequality constraint.
Step 4) If j=n-1, then go to Step 5; otherwise j=j+1and go to Step 2.
Step 5) the value of the last element of an individual is determined by subtracting 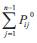 from the total system demand. If the value is in the range of its operating region then go to Step 6; otherwise go to Step 1.
from the total system demand. If the value is in the range of its operating region then go to Step 6; otherwise go to Step 1.
Step 6) Stop the initialization process.
For creating each individual while satisfying equality and inequality constraint the following strategy has been used.
Pmin+(Pmax-Pmin) x rand(1)
rand (1) is a MATLAB function which produces a value in between 0 and 1.
After creating the initial position of each individual, the velocity of each individual is also created at random. The following strategy is used in creating the initial velocity.
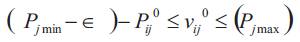
Where ω is a small positive real number. The velocity of element j of individual 'i' is generated at random within the boundary. The difference is the upper limit in eqn (8) i.e., the maximum limit of velocity is equals to the maximum limit of position.
(i). Velocity update
To modify the position of each individual, it is necessary to calculate the velocity of each individual in the next stage. In this velocity updating process, the values of parameters such as , c1 , c2 should be determined in advance. The constriction factor
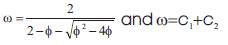
The values of c1 and c2 have the same value, which implies the same weights are given between Pbest and Gbest in the evolution processes. The velocity of each particle in the next stage can be updated by using eqn (6).
(ii)Position modification
The position of each individual is modified by eqn (7). The resulting position of an individual is not always guaranteed to satisfy the inequality constraints due to over/under velocity. If any element of an individual violates its inequality constraint due to over/under speed then the position of the individual is fixed to its maximum/minimum operating point as shown in Figure 4. Therefore, this can be formulated as eqn (10).
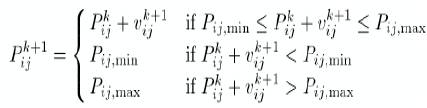
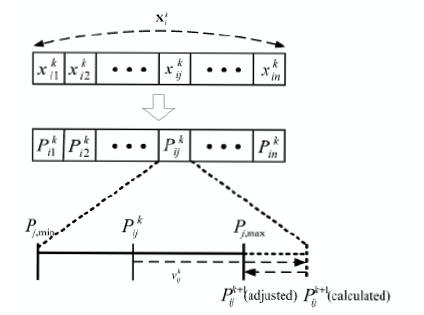
Figure 4. Adjustment strategy for an individual's position within boundary
Although the aforementioned method always produces the position of each individual satisfying the inequality constraints in eqn (3), the problem of equality constraint still remains to be resolved.
Therefore, it is necessary to develop a new strategy such that the summation of all elements in an individual (i.e.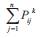 , ) is equal to the total system demand. To resolve the equality constraint problem without intervening the dynamic process inherent in the PSO algorithm, we propose the following heuristic procedures.
, ) is equal to the total system demand. To resolve the equality constraint problem without intervening the dynamic process inherent in the PSO algorithm, we propose the following heuristic procedures.
Step 1) Set j=1. Let the present iteration be k.
Step 2) Select an element (i.e., generator) of individual i at random and store in index array A(n).
Step 3) Modify the value of element j using eqns (6),(7),and(10).
Step 4) If j= n-1 then go to Step 5, otherwise j=j+1 and go to step (2)
Step 5) The value of the last element of individual is determined by subtracting 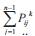 from PD . If the value is not within its boundary then adjust the value using eqn (12) and go to Step 6, otherwise go to Step 8.
from PD . If the value is not within its boundary then adjust the value using eqn (12) and go to Step 6, otherwise go to Step 8.
Step 6) Set l=1 .
Step 7) Readjust the value of element 'l' in the index array A(n) to the value equality condition (i.e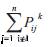 . ). If the value is within its boundary then go to Step 8; otherwise, change the value of element 'l' using eqn 10. Set l=l+1, and go to Step7. If l=n+1, go to Step 1.
. ). If the value is within its boundary then go to Step 8; otherwise, change the value of element 'l' using eqn 10. Set l=l+1, and go to Step7. If l=n+1, go to Step 1.
Step 8) Stop the modification procedure.
The Pbest of each individual i at iteration k+1 is updated as follows.
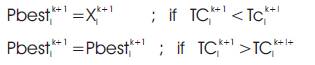
To accelerate the convergence speed to the solutions, the IPSO has introduced the search space reduction strategy. This strategy is activated in the case when the performance is not increased during a pre-specified iteration period. In this case, the search space is dynamically adjusted (i.e., reduced) based on the distance between the Gbest and the minimum and maximum output of generator. To determine the adjusted minimum/maximum output of generator j at iteration k, the distance is multiplied by the predetermined step-size and subtracted /added from the maximum (minimum) output at iteration as described in eqn. (12).
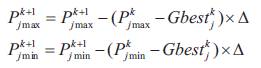
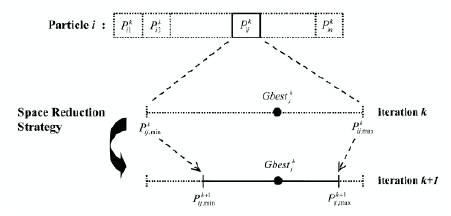
Figure 5. Schematic of the dynamic space reduction strategy.
The IPSO is terminated if the iteration approaches to the predefined maximum iteration.
There exist several parameters to be determined for the implementation of the PSO. In this paper these parameters have been determined through the experiments for the 3-generator system. To avoid the problem of the curse of dimensionality, the procedures and strategies are determined as follows:
i) The values of and have the same value, which implies the same weights are given between Pbest and Gbest in the evolution processes.
ii) Number of particles (10-50) are reported as usually sufficient.
iii) Usually c1 +c2 =4, no good reason other than empiricism.
iv) If Vmax is too low the IPSO convergence speed is too slow; if Vmax is too high, IPSO performance is too unstable.
v) The values of are also varied from 0.01to 0.8 with increments of 0.01 under the assumption that the parameters c1 and c2 are tuned in the processes.
To assess the efficiency of the proposed IPSO, it has been applied to ED problems where the objective functions can be either non-smooth with valve point loading and multi fuel effect. The results obtained from the IPSO are compared with the existing methods such as evolutionary programming (EP) [3] and the genetic algorithm (GA) [5].
The IPSO is applied to two ED problems, one with 3 generators and another with 13 generators, where valvepoint effects are considered for both problems. The input data for 3-generator and 13 generators are given in [6]. Here, the total demand for the 3-generator and 13- generator systems is set as 850 MW, 1800 MW respectively. The obtained results for the 3-generator system using the predetermined parameters are given in Table 1. and the results are compared with the existing methods. It shows that the IPSO has succeeded in finding the global solution presented in [3] with a high probability always satisfying the equality and inequality constraints.
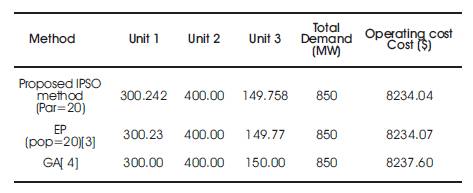
Table 1. Test results of 3 generators system
The convergence characteristics of IPSO for the three generator system with different number of particles are shown in Figure 6. From these characteristics it is observed that as the number of particles increases the convergence performance of PSO is improved. So with constriction factor is tested on the same example with valve point effects. These results are compared with weight factor results. From the Figure 7, it has been observed that the convergence speed of the IPSO is improved with constriction factor.
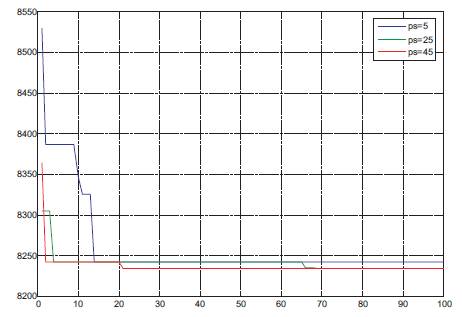
Figure 6. illustrates the convergence characteristics of the proposed PSO for different number of particles
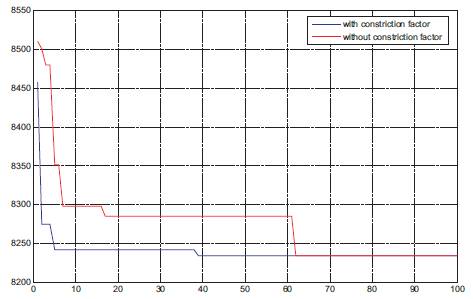
Figure 7. Convergence characteristics with and without constriction factor
The proposed algorithm is also tested on 13-generator system considering valve point effects. Generator coefficients, maximum demand and generator output limits are given in[3]. The optimum operating policy of the generators is determined and the results compared with the results obtained from Evolutionary programming. The results are given in Tables 2 and 3.

Table 2. The optimum operating policy of 13 generators

Table 3. Test results of 13 generator system
The developed IPSO has also been applied to the ED problem with 10 generators where the multiple-fuel effects are considered. In this case, the objective function is represented as the piecewise quadratic cost function. The input data and related constraints of the test system are given in [5]. In this case, the total system demand is 2500MW.
The minimum cost is calculated by taking the mean value of the results obtained from 20 random trials and results are compared with the results of evolutionary program method [3] and are given in Tables 4 and 5.

Table 4. Optimum operating policy of the generators
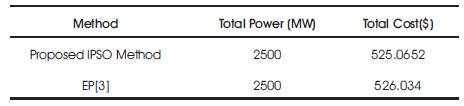
Table 5. Test results of 10 generator system considering multi fuel point effects
The IPSO has provided the global solution satisfying the constraints with a very high probability for the ED problems with smooth cost functions. For the ED problems with nonsmooth cost functions due to the valve-point effects, the IPSO has also provided the global solution with a high probability for 3-generator system which are better than other heuristic methods. In the case of non-smooth function problem due to multi-fuel effects, the IPSO has shown superiority to the numerical methods, the evolutionary programming approach, while providing very similar results.
The PSO algorithm with the constriction factor can be considered as a special case of the algorithm with inertia weight. From the simulation results, it can be concluded that the best approach to use with particle swarm optimization as a "rule of thumb" is to utilize the constriction factor approach while limiting Vmax to Xmax .