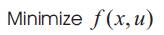
A new approach to solve optimal power flow (OPF) problem in the power system is presented. In the proposed method, a two step initialization process have been adopted which eliminates the mutation operation and also it gives optimal solution with less number of generations which results in the reduction of the computation time. The feasibility of the proposed algorithm is demonstrated for a standard 2-machine, 5-bus system. The obtained results using proposed method are compared with the conventional optimization technique. The results reveal better solution and computational efficiency of the proposed algorithm.
In the optimal power flow problem, certain control variables are adjusted to minimize an objective function such as the cost of active power generation or losses while satisfying operating limits on various control and dependent variables. The solution of OPF problem must satisfy the network security constraints. In the past, conventional methods like Newton's method[1-3] and Interior point method [4-6] were used to solve the OPF problem. But, in recent years, evolutionary methods are commonly used to solve the OPF problem than conventional methods because of their advantages like simple to implement, reduction in computation time, a fast and near global optimal solution.
A novel approach for the optimal power flow problem in a deregulated power market using Bender's decomposition has been presented[7-9]. The other methods to find the solution for OPF problem have been discussed[10-13]. In this paper the initialization is done in two steps so that the mutation operation is not required and also it gives better solution with less number of generations which results in the reduction of the computation time. The feasibility of the proposed algorithm is demonstrated for a standard 2- machine, 5-bus system. Then, the obtained results are compared with Newton's method. From the results, it can be observed that the proposed method gives better solution than the Newton's method.
The rest of the paper is organized as follows: Section 2 explains the optimal power flow problem formulation. Section 3 describes the proposed algorithm. Section 4 demonstrates the effectiveness of proposed algorithm for optimal power flow solution through numerical examples and finally, conclusions are given in section 5.
In its general form, the OPF problem can be mathematically represented as
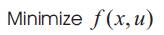

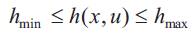
where,
f (x, u) is the objective function
x is the vector of dependent variables
u is the vector of independent or control variables
g (x, u) represents equality constraints
h(x, u) represents inequality constraints
In this article, minimization of fuel cost is considered as an objective function to examine the performance of the proposed algorithm. The optimal solution must satisfy the equality and inequality constraints. The total fuel cost function for a number of thermal generating units can be represented by a quadratic function as
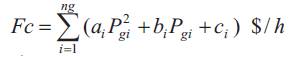
where,
ai ,bi & ci are cost co-efficients of generator at bus i
Pgi is the generation of the ith generator.
ng is the number of generator buses.
The equality constraints represent the set of nonlinear power flow equations as
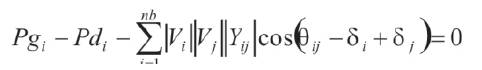
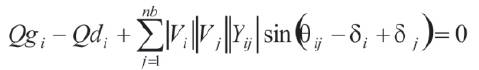
where
Pgi & Qgi are the active and reactive power generations at ith bus. Pdi & Qdi are the active and reactive power demand at ith bus.nb is the number of buses.Vi & Vj are the voltage magnitudes of ith & jth bus. δi & δj are the voltage angles of ith & jth bus. !Yij ! & θ ij are the bus admittance matrix elements between ith & jth bus.
The following are inequality constraints for OPF problem
Generators real and reactive power constraints
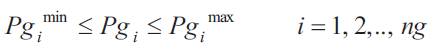
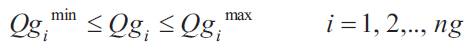
where Pgimin & pgimaxare the minimum and maximum active power generation limits at ith bus . Qgimin & Qgimax
are the minimum and maximum reactive power generation limits ith at bus.
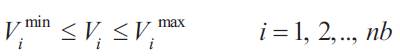
where Vimin &Vimax are the minimum and maximum voltage limits at ith bus
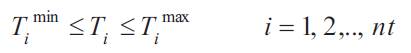
where Timin & Timax are the minimum and maximum tap settings of ith transformer nt and represents number of transformer tap settings.
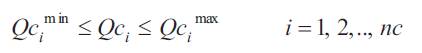
where Qcimin & Qcimax are the minimum and maximum reactive power injection limits of ith compensator and nc represents number of compensators.
The intelligent search evolution algorithm tries to approach the target in an optimal manner for finding the optimal or near optimal solution to any mathematical optimization problem. The initial population is randomly generated with the control parameter limits in two steps. Then, the evolutionary operators like crossover or recombination and selection are performed to all individuals until a stopping criterion is reached. The major stages of the proposed algorithm are briefly described as follows:
The population is generated for each control variable by using the following equation
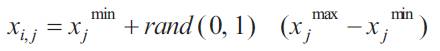
where i=1, 2,.., ps j=1, 2,.., ncv.
ps = population size.
ncv = number of control variables.
xjmin & xjmax are the lower and upper bounds of jth control variable.
r and ( 0,1 ) is a uniformly distributed random number between 0 and 1.
The two step initialization process provides better probability of detecting an optimal solution to the power flow equations that would globally minimize a given objective function. In the first step, initial population is generated as a multi-dimensional vector of size (ps × ncv) and it is considered as a village. Evaluate the value of cost function for each string in the village. Select the best string from the village corresponding to minimum cost. Repeat the procedure for number of villages (nv). In the second step, combine all the best strings from each village to form multi-dimensional vector of size (nv ×ncv) and this new population is used for evolutionary operations.
In this study, an efficient recombination operator has been used so that search along variables is also possible. If xi(j)and xi (k)are the values of variables xi in two strings j and k. The crossover between these two values may produce the following new value
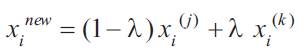
where the parameter λ is a random number between 0 and 1.
For the present work, sorting and ranking selection procedure is used.
In the current work, the number of generations reaches the given maximum number of generations is used as stopping criteria.
A standard 2-machine, 5-bus system [14] has been considered to demonstrate the effectiveness and robustness of the proposed method. A MATLAB program is implemented for the test example on a personal computer with Intel Pentium dual core 1.73 GHz processor and 512 MB RAM. Ten runs have been performed for the test example. The optimal solution results over these ten runs have been tabulated. The input parameters of the proposed method for the test example are given in Table1.
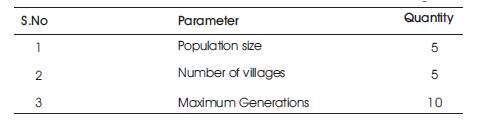
Table 1. Input Parameters for the test Example
In 5-bus test system, bus 1 is considered as slack bus, while bus 2 as generator bus and other buses are load buses. The solution for the optimal power flow problem is obtained using proposed method and is compared with the solution given in example 7.3.6 [14] which is solved using Newton's Method. The comparison of bus voltages and power flows of test example for both the methods are given in Table 2 and Table 3 respectively. The optimal power flow solution results of both the methods are given in Table 4. The convergence characteristics of this test example using proposed method are shown in Figure1.
From Table 2 and Table 3, it can be observed that the voltage magnitudes, voltage angles, the active power flow and reactive power flow obtained using the proposed method is close to Newton's Method. Also, from Table 4, it is clear that the total power generation, total losses and cost computed using the proposed method is close to Newton's Method. Further, as the number of iterations increase, the cost decreases and it is nearly constant above 5 iterations as shown in Figure.1 which indicates that the number of iterations required for the proposed method is less.
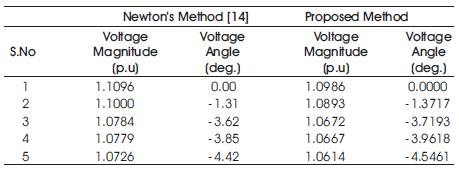
Table 2. Comparison of bus Voltages for the 5-bus System
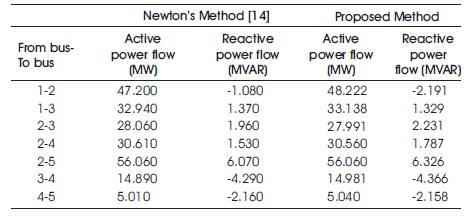
Table 3. Comparison of power flow for the 5-bus system
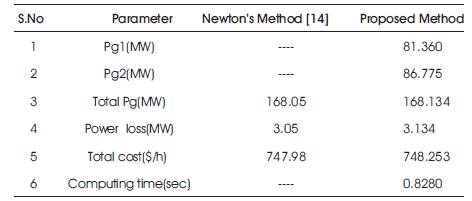
Table 4. Comparison of OPF Results for the 5-bus System
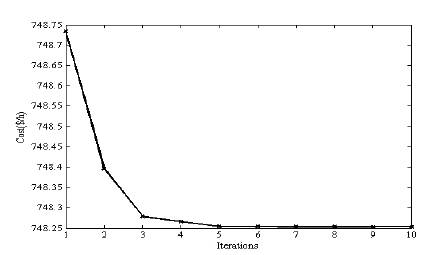
Figure 1. Convergence Characteristics of Standard 5 bus system using Proposed Method.
The Newton's method for optimal power flow solution is more complex because, it needs a Jacobian matrix [J], Hessian matrix [H] and inverse of Hessian matrix. As the system size increase, it is more difficult to form these matrices and to find the inverse of Hessian matrix. Because of this, it takes more computation time and more number of iterations for best solution. These problems can be overcome by using the proposed method which is less complex compared to Newton's method. From the test example results, it is very clear that the optimal solution obtained using proposed method is close to the Newton's method but it requires less number of iterations. The less number of iterations for optimal solution indicates reduction in the computing time. This is because of two step initialization process adopted in the proposed method which also eliminates mutation operation.
In this paper, an intelligent search evolution algorithm has been proposed. The proposed method employs a two step initialization process and there is no need of mutation operation. The results demonstrate the effectiveness and robustness of the proposed method. The results obtained for test example using the proposed method are compared with Newton's method and observations reveal that the results are close to the Newton's method. Also, it is clear that the proposed method gives optimal solution with less number of generations and requires less computation time.