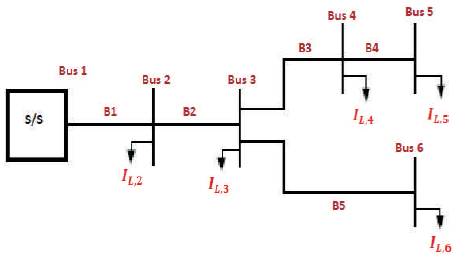
Figure 1. A Sample 6-bus Radial Distribution System
This manuscript proposes a novel technique to solve the feeder reconfiguration problem with an objective of minimizing total real loss and maximizing energy savings in a radial distribution system. Feeder reconfiguration (FRCG) is a significant way of altering the power flows through the lines or to alleviate the overloads on the feeders, while maintaining the radial structure. To ensure the radial nature and avoid islanding of nodes, all feasible switching combinations are formed prior to the optimization process using a graph theory. This FRCG problem enables for determining the best combination of switches are to be opened for maximum loss reduction and energy savings, so it offers optimal performance. A Metaheuristic Whale Optimization (WOA) Algorithm is used to reconfigure and identify the optimal secure switches for maximum real power loss reduction, which directs to energy savings in the main distribution system. The constraint of real power loss is incorporated into the estimation of the objective function. The anticipated method has been examined on standard 33-node and 119-node systems at regular load pattern, where attained results are compared by means of available literature.
Reconfiguration is defined as a change in the structure of the system without disturbing the loads or without islanding of any nodes in the original system. Feeder Reconfiguration (FRCG) of radial distribution system is a very successful approach to reduce losses, improve voltage profile, and enhance system reliability. Distribution networks are generally structured in mesh, but operated in a radial configuration for effective coordination of their protection schemes and to reduce the fault level. The primary objective of network reconfiguration is to acquire an open loop configuration that minimizes real power loss while satisfying all the operational constraints without islanding any node.
A number of research papers have been emerged on the general topic of feeder reconfiguration, where there is still a need to develop more appropriate and effective techniques for the network reconfiguration under reliable operating conditions. Many recent researches have been done on distribution feeder reconfiguration on reducing the power losses. Das et al. (1995) proposed a simple and efficient method for solving radial distribution networks, which involves only the evaluation of a simple algebraic expression of voltage magnitudes and no trigonometric functions as opposed to the standard load flow case. Shirmohammadi and Hong (1989) proposed an algorithm of distribution feeder reconfiguration to reduce line resistive losses. Goswami and Basu (1992) presented a heuristic algorithm for feeder reconfiguration.
Haque (1999) described a scheme to reduce the I R loss correlated with the reactive component of the branch currents by installing the shunt capacitors at proper locations. Mishima et al. (2005) proposed a tabu search for reconfiguration of an open loop radial distribution network with distributed generators to minimize the total line losses subjected to the line or transformer capacity constraints and voltage constraint. Gomes et al. (2005) proposed a heuristic optimization technique suited for network reconfiguration to minimize total system losses in the primary distribution system. Here one node was isolated from the original network during switching.
Zhang et al. (2007) presented an Improved Tabu Search (ITS) algorithm for loss minimization reconfiguration in large-scale distribution systems. Reddy and Reddy (2010) propose a fuzzy based two stage analytical approach used for the capacitor placement in the reconfigured network. Niknam (2010), and Niknam and Nayeripour (2010) presented a hybrid PSO-ACO and modified SFLA of distribution system reconfiguration for loss reduction. Gupta et al. (2011) described an Adaptive PSO (APSO) for reconfiguration of radial distribution system for minimization of real loss without involving any additional cost concerned switching equipment. Srinivasa Rao et al. (2011) proposed an optimal reconfiguration problem for large scale networks to reduce total network losses using GA, RGA, ITS, and HSA algorithms. Abdelaziz et al. (2013)proposed a feeder RCG solved by two optimization methods to find the suitable topology of an explicit load, which minimizes the total system power loss subjected to voltage limits, branch current limits, and radial structure.
Sedighizadeh et al. (2014) described simultaneous network RCG and placement of capacitors at suitable locations to reduce emissions. Imran and Kowsalya (2014) proposed a new Fireworks Algorithm to solve network RCG problem for different abnormal conditions. Reddy and Reddy (2016a) described the dragonfly algorithm exclusively for sequential and simultaneous network reconfiguration to acquire minimal loss configuration. Reddy and Reddy (2016b) proposed PSO algorithm using sequential and simultaneous network reconfiguration to accomplish lowest loss configuration. Mirjalili and Lewis (2016) developed a new nature motivated metaheuristic optimization algorithm called Whale Optimization Algorithm (WOA), which mimics the social behaviour of humpback whales.
Namachivayam et al. (2016) proposed loss reduction and utility's loss of returns by network reconfiguration and capacitor placement. Reddy and Reddy (2017a) proposed ALO of capacitor placement after reconfiguration for loss reduction. Reddy et al. ((2017b), (2017c) )proposed the application of the Grey Wolf Optimization (GWO) and Sine Cosine Algorithm (SCA) of network reconfiguration for loss reduction.
The main contributions of this paper are as follows.
A number of researchers have proposed backwardforward sweep method for balanced radial distribution systems power flow analysis. In backward state, Kirchhoff's Current Law (KCL) is applied to calculate the branch currents from load currents and Kirchhoff's Voltage Law (KVL) is applied to find the voltages of each node for each upstream node of a line, i.e., in forward stream. A sample 6-bus system is shown in Figure 1.

Figure 1. A Sample 6-bus Radial Distribution System
The complex power injected into the bus n is given by,
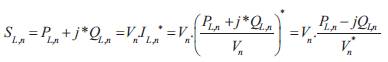
The relation between load currents and branch currents can be found by using KCL equations (Gupta et al., 2011) as follows.
Thus, the relationship between load currents and branch currents expressed in Bus-Injection to Branch-Current (BIBC) matrix form is given as,
The receiving end voltages can be calculated by forward sweeping across the line by subtracting the line section drop from the sending end voltages of the line section. The relation between the branch currents and bus voltages can be obtained by following equations (Gupta et al., 2011) .
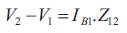
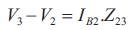
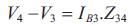
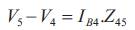
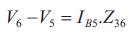
The above equations signified in the reduced matrix structure (Gupta et al., 2011) is specified in general form as,
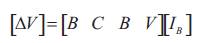
The load end voltages can be studied by forward sweep across the branch by deducting the line section (branch) drop from the source end voltages of that same branch.
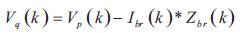
The total real power losses in the distribution systems are 2 active and reactive power losses. The total real loss (I R loss) in a balanced distribution system is given as,
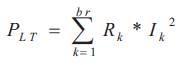
The constraints considered are as follows.
Power balance constraints,
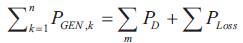
Voltage constraints,
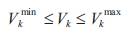
Here, the acceptable voltage limits are 0.9-1.10 for the given system.
The objective function of the problem is to minimize the total real power loss in the primary distribution system, which is given as,
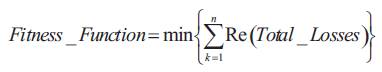
The maximum energy savings per year (Sedighizadeh et al., 2014) is given as,
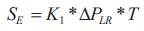
where, SE is the net savings in $ / year;
K1 is a factor that the energy losses are converted into dollars;
T is the Total time period of hours in a year; and
DPLR is the system’s real power loss reduction in Kilo Watts.
The fundamental loops are determined for the meshed distribution network by closing all tie switches. The number of fundamental loops in the meshed distribution network is equal to the number of tie-switches of the system and are given by the relation (Gupta et al., 2011).
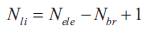
where, Nii is the total number of links or tie switches;
Nele is the total number of elements, i.e., sectionalizing plus ele tie-switches; Nbr is the total number of branches.
Switching loops are designed by considering the real power loss constraint as given in Table 1.
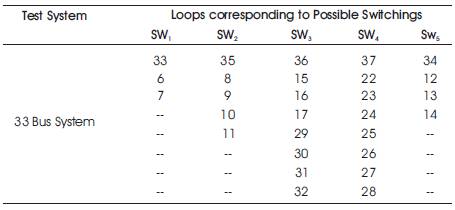
Table 1. Switching Reconfiguration of 33 Bus
Basic configuration for 33-bus system = [33 34 35 36 37].
Here, simultaneous switchings are used for the optimal switching corresponding to minimum loss in each loop, while maintaining the radial structure in the distribution systems (Abdelaziz et al., 2013).
Population-based meta-heuristic optimization algorithms share a common feature regardless of their nature. “The search process is divided into two phases: exploration and exploitation. The optimizer must include operators to globally explore the search space. In this phase, movements should be randomized as largely as possible.
The exploitation phase follows the exploration phase and can be defined as the process of looking over in every aspect the promising regions of the search space. Exploitation concerns to the local search capability in the promising regions of design space found in the exploration phase. Finding a good balance between exploration and exploitation is the most challenging task in the development of any meta-heuristic algorithm due to the stochastic nature of the optimization process” (Mirjalili and Lewis, 2016). Surprisingly, WOA comprises of two internal parameters to be tuned, i.e., A and C. The shrinking encircling mechanism is shown in Figure 2 and the spiral updating position approach is exposed in Figure 3.
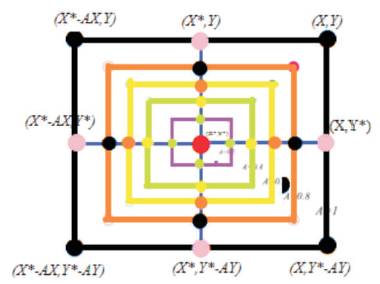
Figure 2. Bubble-net Search Mechanism employed in WOA: Shrinking Encircling Mechanism
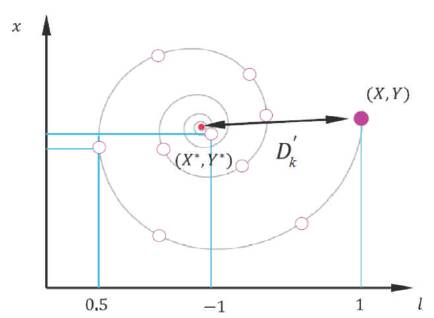
Figure 3. Update the Spiral Position
The mathematical model of WOA is described as,
Step 1: Initialize the number of search agents=100, maximum iterations=500.
Step 2: Set boundaries, i.e., lower, upper boundaries and dimensions to the necessary parameters.
Step 3: Perform the basic load flow to acquire the actual I2 R loss and voltages prior to the optimization.
Step 4: Initialize position vector to zero and set score for the leader to infinite. Randomly generate an initial whale position X.
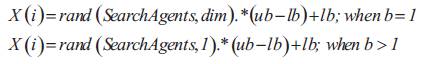
Step 5: Update a, A, C, l, and p for every iteration.

Here r1 and r2 are random numbers in the range [0, 1]
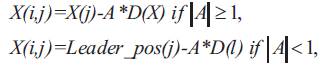
Step 6: Verify boundary conditions of whales in the search space and set back them if they are out of the boundary.
Step 7: A spiral equation is then created between the position of whale and prey to mimic the helixshaped movement of humpback whales as,
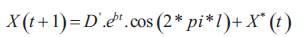
Step 8: The humpback whales swim around the prey within a shrinking circle and along a spiral-shaped path simultaneously. The shrinking encircling mechanism or the spiral model updates the position of whales during the optimization process.
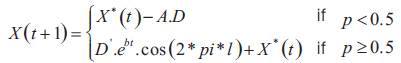
Step 9: In exploitation phase, updating the position of each search agent according to a randomly selected search agent instead of the best search agent created so far. This mechanism and | A | > 1 emphasize exploration and allow the WOA algorithm to perform a global search.
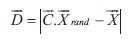
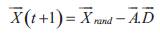
Step 10: Repeat the iterative process from step 6 to 9 until the iteration count terminates or achieves an optimum solution.
Step 11: Display the leader score of whale, which gives the optimum result is power loss with respect to leader position or set of best switches corresponding to the low loss configuration.
The proposed whale optimization is applied on standard 33-node and 119-node systems. In all calculations, the parameters are, K = 0.06/ kWh; T = 8760hr / year.
This system is configured with a 100 MVA, 12.66 KV standard 33-node test system with 37 branches, 32 sectionalizing switches and 5 tie switches. The total substation loads for the basic configuration are 4715 kW and 2300 kVAr ( Haque, 1999); Reddy et al., 2008. The simultaneous reconfiguration results for 33-bus system are shown in Table 2. The voltage profile of original network and after feeder reconfiguration is shown in Figure 4.

Table 2. Feeder Reconfiguration Results of 33-node Systems
Figure 4. Comparison of Voltage Profile before and after Reconfiguration of Normal Load Conditions of 33-node System
From Table 2, the real power loss for the original network was 369.2558 kW and after feeder reconfiguration by the application of WOA algorithm, power loss is reduced to 238.2888 kW.
The configuration of 100 MVA, 11 kV, standard 119-node test system with 133 branches, 118 sectionalizing switches and 15 tie switches. The total substation load of the basic configuration is 22.7097 MW and 17.0411 MVAr ( Zhang et al., 2007; Rao et al., 2011
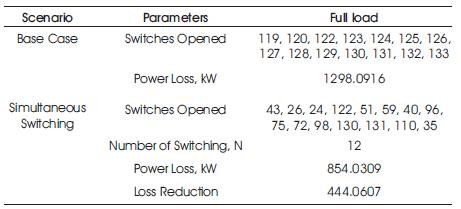
Table 3. Feeder Reconfiguration Results of 119-node Systems
The voltage at each node of the original and after optimal configuration of 119-node system is exposed in Figure 5. The comparison results with published articles in the literature of 119-node system are revealed in Table 4.
Figure 5. Comparison of Voltage Profile before and after Reconfiguration at Normal Load Conditions of 119-node System
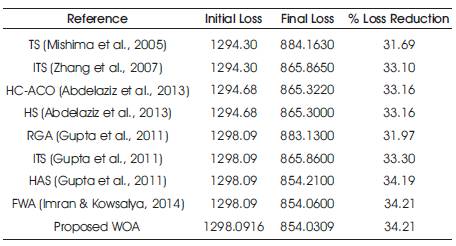
Table 4. Comparison Results of 119-node Systems
From Table 3, the real power loss for the original network was 1298.0916 kW and after feeder reconfiguration using the application of WOA algorithm, power loss is reduced to 854.0309 kW. The comparison of initial, final loss, loss reduction, and energy savings of original and reconfigured network are exposed in Table 5.
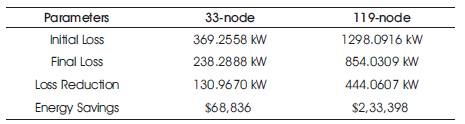
Table 5. Energy Savings of 33-node and 119-node Systems
The annual energy savings with simultaneous network reconfiguration are $68,836 for 33-node system and $2,33,398 for 119-node system, respectively.
The performance of whale optimization of 33-node test system is compared with different optimization techniques published in available literature, which is exposed in Table 6. Here, all algorithms are simulated for maximum iterations=500 and search agents=100.
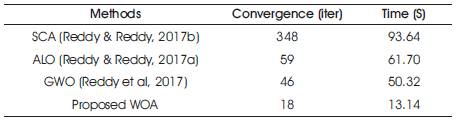
Table 6. Comparison of Different Algorithms on 33-node System
In this paper, Feeder Reconfiguration is implemented in two standard distribution systems using simultaneous switching. The optimal network reconfiguration is to find a better configuration of open loop network that gives lowest power loss. In this paper, the whale optimization algorithm is successively applied for reconfiguration problem to reduce total real power losses and it takes less computational time. The maximum loss reduction after feeder reconfiguration is 130.9670 kW for 33-node and 444.0607 kW for 119-node systems, respectively. The reduction in power losses is maximum, which leads to maximize energy savings with simultaneous switching.
The power loss reduction after feeder reconfiguration compared to the original network is 35.47% for 33-node and 34.21% for 119-node systems, respectively. The energy savings are $68,836 for 33-node system and $2,33,398 for 119-node systems, respectively. The numerical results illustrate that the proposed whale optimization algorithm is capable of finding optimal solution with respect to best set of switches using simultaneous switching.