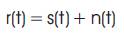
Modulation scheme is one of the most important characteristics to note in the monitoring activity and identification of radio signals. Modulation recognition system must be able to make the correct classification of the modulation scheme of the received signal under interference. AMR is required in both military and civilian applications, such as surveillance, electronic warfare, threat assessment, signal confirmation, interference identification, software defined radio, and spectrum management. AMR is also believed to play an important role in the implementation of the 4th-Generation (4G) communication system. A generalized modulation identification scheme is developed and presented. With the help of this scheme, the automatic modulation classification and recognition of digitally modulated speech signals with a priori unknown parameters are possible effectively. The developed scheme based on wavelet transform and statistical parameters has been used to identify M-ary PSK, M-ary QAM, and M-ary FSK modulations. Various speech signals corrupted by noise have been used as sample signals .Statistical parameters are calculated and compared against certain threshold values to detect the modulation type. The simulated results show that the correct modulation identification is possible to a lower bound of 15 dB.
Broad Area: Electronics& Tele Communication Engineering.
Sub Area: Digital Signal Processing.
The automatic recognition of the modulation format of a detected signal, the intermediate step between signal detection and demodulation, is a major task of an intelligent receiver, with various civilian and military applications. Obviously, with no knowledge of the transmitted data and many unknown parameters at the receiver, such as the signal power, carrier frequency and phase offsets, timing information, etc., blind identification of the modulation is a difficult task. This becomes even more challenging in real-world scenarios with multipath fading, frequency-selective and time-varying channels. High-level amplitude modulated signals M-ASK M-FSK, MQAM etc. have an excessive number of symbol status and therefore incline to be disturbed by noise. So it is difficult to identify the high-level amplitude modulated signals at low SNR.
Automatic identification of the digital modulation type of a signal is a rapidly evolving area [1]. The techniques are proposed to distinguish digitally modulated signals such as Quadrature Amplitude Modulation(QAM) signal, Phase Shift Keying(PSK) signal and Frequency Shift Keying(FSK) signal [2] .The features for identification may be either time based or frequency based. Time domain features may be amplitude , instantaneous frequency or phase of complex envelop of modulated signal In frequency domain power spectrum may be analyzed or parameters such as variance skewness, etc may be analyzed. [3] [4]. Counts of signals falling into different parts of the signal plane are used to identify the digital modulation types. These methods are either computationally intensive or require a high carrier-to-noise ratio (CNR). Another approach for digital modulation types identification is to use wavelet transform (WT) [5-10]. Under the assumption that some communication parameter such as carrier frequency and symbol rate are available, another technique used is an approximate likelihood ratio modulation classifier to separate BPSK and QPSK[11-13].
Artificial neural network approach has been applied to classify identification schemes[14].
This paper proposes modulation identification scheme for recognition of digitally modulated signals using transients. In ideal case, the Haar WT magnitude (jHWTj) of a PSK signal is a constant and that of a FSK signal is a multistep function. Hence the variance of jHWTj of an input signal is used as a feature to classify the two signals.Compared to PSK and FSK signals, one distinction in QAM signal is that it does not have a constant amplitude. The jHWTj of a QAM signal is a multi-step function similar to that of a FSK signal because of the change in amplitude as symbol changes. Histogram peak count technique is used to distinguish the modulated signals for varying SNR's.
Two general classes of AMC algorithms can be crystallized, Likelihood-Based (LB) [11-13] and Feature- Based (FB) [14-15] methods, respectively. The former is based on the likelihood function of the received signal and the decision is made comparing the likelihood ratio against a threshold. A solution offered by the LB algorithms is optimal in the Bayesian sense, viz., it minimizes the probability of false classification. The optimal solution suffers from computational complexity. In the FB approach, on the other hand, several features are usually employed and a decision is made based on their observed values. Once the modulation format is correctly identified, other operations, such as signal demodulation and information extraction, can be subsequently performed.
Different modulation schemes have the characteristic of different transients in amplitude, frequency or phase. The wavelet transform (WT) is a powerful tool for analyzing nonstationary signals, which include digital communication signals, and the WT magnitude of communication signals vary with modulation types. The WT has capability to extract transient information which can be exploited for modulation classification.
Let the received waveform r(t), 0 ≤ t ≤ T be described as
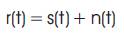
where,
s(t) is transmitted signal and n(t) is an additive white Gaussian channel noise. The signal s(t) can be represented in complex form as
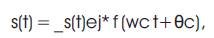
where,
ωc is the carrier frequency and θc is the carrier phase. Generally, the complex envelope of s(t) in (1) may be expressed for all modulation types as
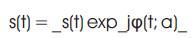
where,
φ(t; a) represents the time-varying phase of the carrier, a represents all possible values of the information sequence {ak}, in the case of binary symbols ak = ±1.
The analysis technique is required for non stationary signal, which will analyze the signal frequency with time instants of occurring. The Fourier transform approach gives either the frequency components or time components. The wavelet transform has the special feature of multi resolution analysis (MRA), which provides the necessary parameters to extract the feature of the modulated signals. The DWT of a signal x is calculated by passing it through a series of filters. First the samples are passed through low pass filter. with impulse response g resulting in a convolution of the two:
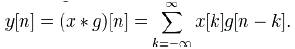
The signal is also decomposed simultaneously using a high pass filter h. The outputs give the detail coefficients (from the high-pass filter) and approximation coefficients (from the low-pass). It is important that the two filters are related to each other and they are known as a quadrature mirror filter.
However, since half the frequencies of the signal have now been removed, half the samples can be discarded according to Nyquist's rule. The filter outputs are then subsampled by 2.
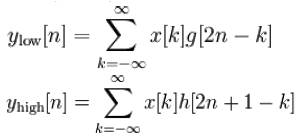
This decomposition has halved the time resolution since only half of each filter output characterizes the signal. However, each output has half the frequency band of the input so the frequency resolution has been doubled. Figure1.
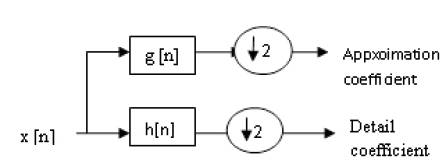
Figure 1. Block Diagram of Filter Analysis
With the sub sampling operator
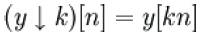
the above summation can be written more concisely.
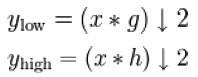
This decomposition is repeated to further increase the frequency resolution and the approximation coefficients are decomposed with high and low pass filters and then down-sampled.
Input signals used here are audio signals corrupted by noise standard modulated signals. There are also Input signals used here such as audio signals corrupted by noise. Standard modulated signals can also be generated using software tools of MATLAB or using Communication Block set of Simulink.
The proposed modulation identification scheme is shown in Figure 2. The identification has been done using statistical parameters. Digitally modulated signal corrupted by noise is used as input signal. Code is developed to extract features such as mean and variance for the signal. Histogram is plotted for various input signals and then peaks are generated. Based on the peaks, decision is taken. Since the transient characteristics of M-ary QAM and M-ary PSK signal are constant it will have single peak in its histogram but the Mary FSK signals have more than single peak because these signals have multistep frequency component .
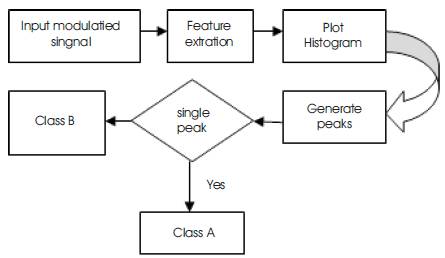
Figure 2. Identification Algorithm
Signals are further classified as that belonging to Class A and Class B, based on threshold values decided based on number of signals. Signals falling in class A and class B has been shown in Table 1. Further classification of signals belonging to class A based on comparison of statistical values with threshold values is shown in Figure 3. Verification of signals is also done by finding the transient values by applying 1D wavelet transform to various modulated signals. The wavelet selected is Haar Wavelet.
Audio wav files corrupted by noise as input signal are tested for classification with the software tools of MATLAB. The developed algorithm is verified for BPSK, 16 PSK, 32PSK, 2QAM, 8QAM, 16QAM, and MFSK modulation schemes. The wavelet transform has been applied to extract the transient characteristics of the received signal. After extracting the transient characteristics, the coefficients were extracted to generate the histogram peak. Figure 4 shows a noisy BPSK Signal. The histogram plot and histogram peak of BPSK is shown in Figures 5 and 6, respectively. These Figures show that M-ary PSK signal has constant transient characteristics, and it has a single peak in its histogram. Figure 7 shows a M-ary FSK signal, its histogram plot Figure 8 and 9 shows multiple peaks as signal have multistep frequency component which distinguishes the two signal.

Table 1. Class distinction of Modulated Signals
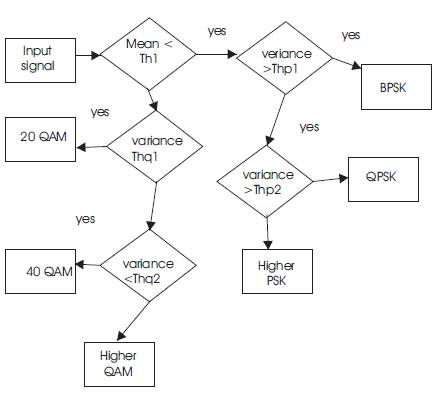
Figure 3. Classification of Class A Type Signals
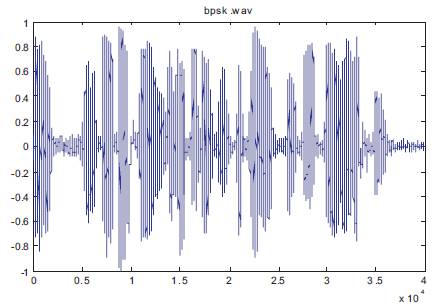
Figure 4. BPSK Waveform Corrupted By Noise
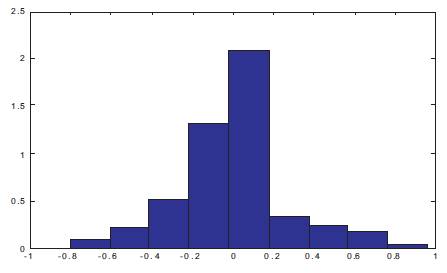
Figure 5. Histogram Plot for BPSK
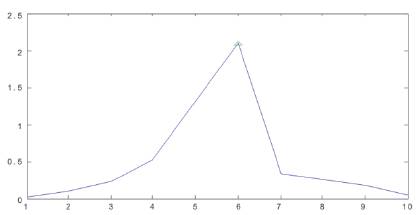
Figure 6. Histogram Peaks for BPSK
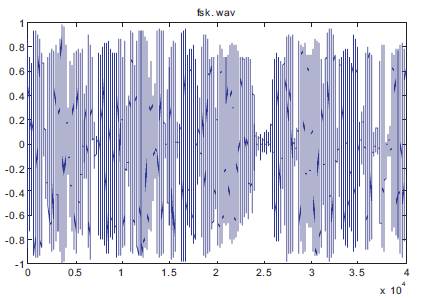
Figure 7. 2FSK Signal Corrupted by Noise
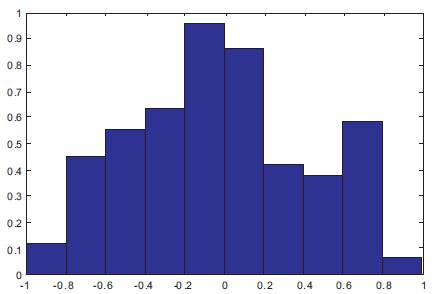
Figure 8. Histogram Plot for 2FSK
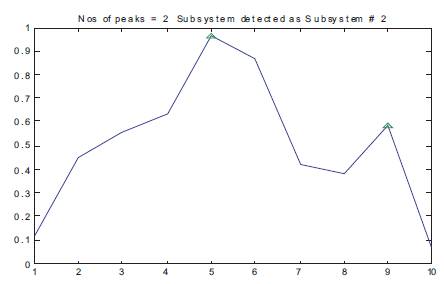
Figure 9. Histogram Peaks for 2FSK
A generalized modulation scheme is described suitable for number of modulation schemes employed in SDR. The algorithm developed is used to test for various audio modulated corrupted signals. The simulated results using wavelet transform technique and statistical parameter measurement shows that correct modulation identification is possible for varying SNR.