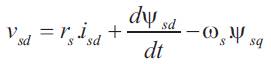
This paper describes the indirect adaptive fuzzy control of doubly fed induction machine with both its stator and rotor fed by two PWM voltage source inverters in which the system operate in stator field oriented control. Associated to Takagi- Sugeno fuzzy model, an indirect adaptive control has been applied to a simplified structure. The development of this model is carried out in two stages. The first stage consists in estimating the parameters of a fuzzy model. In the second, the control is provided by a fuzzy controller based on the torque calculated method. Simulation study based on idealised motor and inverter models is conduced to show the effectiveness of the proposed method.
Many kinds of fuzzy models of control process have been developed to describe the behaviour of complex nonlinear dynamics. In the last decade, a considerable amount of research has focused on the design of adaptive fuzzy controllers. The main advantages of the latter are a better performance, because the adaptive controller can adjust itself to the changing environment, less information about the plant is needed, also the adaptation law can help to learn the dynamics of the plant during real-time operation.
The mathematical model of the DFAM in Park configuration is nonlinear and highly coupled. The control of the DFAM is possible by applying stator field oriented techniques[1-6]. Nevertheless, a uncertain DFAM behaviour and parameters model variations in time yields to degradations of the control performances in the case of an off-line identification. Therefore, it is suitable to look for some adaptive methods[7]. Here in this paper, we propose a new control scheme to achieve the goal of speed regulation with stator field oriented double fed induction motor drive and adaptive fuzzy logic control based on the inverse identification. This one allows a high performance of the control scheme and especially the robustness of the algorithm with regard to changing parameters and external disturbances.
The controlled system is a wound rotor asynchronous motor, fed at both its stator and rotor sides by two PWM voltage source inverters.
Using frequently adopted assumptions, like sinusoidally distributed air-gap flux density distribution and linear magnetic conditions and considering the stator voltages (vsd, vsq) and rotor voltages (vrd, vrq) as control inputs, the stator current (isd , isq ), the rotor current (ird , irq ) and the speed ωm as state variables. In the referential axis linked to m rotating field, the following electrical equations are deduced [1],
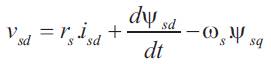
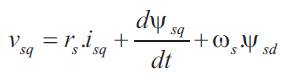
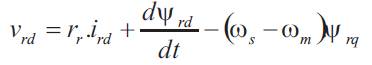
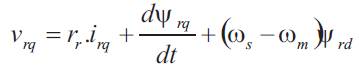
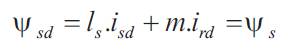

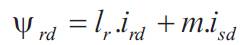
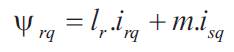
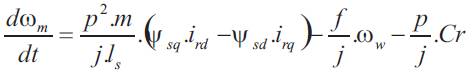
The power factor and stator flux Ψs are dependent on the s direct component of both stator and rotor currents [8-10]. From equations (1) and (5) it follows that unity power factor at stator side, i.e. alignment of voltage and current vectors, will be obtained in steady state by imposing the references:
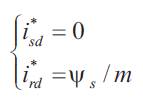
In the case of a rotor flux oriented vector control of a cage induction motor, it is known that the rotor flux follows the dcomponent of stator current only with a large (rotor) time constant. For high dynamic drives the flux has thus to be kept high even at no load.
In a DFAM, the flux is directly related to the d-component of the rotor current and the flux level can be quickly adapted. This allows, if necessary, a flux reduction during no load (economy mode) without too much degrading the torque response.
The controllers for isd and isq are decoupled by introducing the control variables Visd and Vird given by:
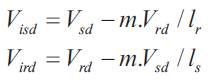
After elimination of the flux (with Ψsq= 0, Ψsd=Ψs ) and the rotor quadrature current, eq. (1) and (3) are transformed into:
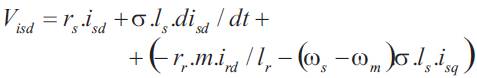
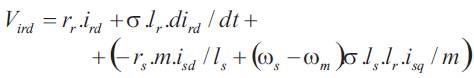
with σ = 1-m2 /(ls lr ) the total leakage coefficient.
The reference values for the direct components of stator and rotor voltages are given by:
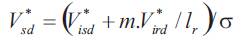
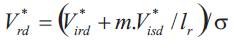
The torque reference C* is transformed into a reference for the q-component of the stator current:
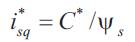
It follows from (4), (6), (7) and (8):
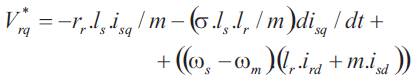
The torque controller generates the reference value for the quadrature component of rotor voltage V*rq.
Finally, the slip or rotor frequency reference is transformed in a reference for the quadrature component of stator voltage eq. (2):
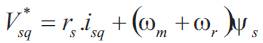
The stator flux position is computed from (eq.3):
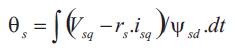
Taking into account the field orientation of the machine, the DFIM equations on d-q axes become:

With taking into account the steady state operation for which the stator flux and the electromagnetic torque are maintained constant equal to their reference values, if the variations of the different current components are neglected, the equations (12),(13) and (17) become:
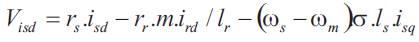
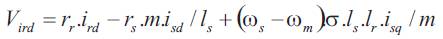
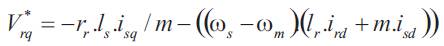
The scheme of the proposed control is shown in Figure 1.
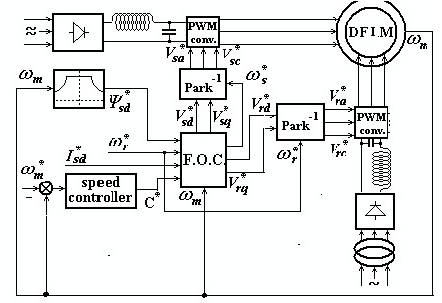
Figure 1. Scheme of the Simplified Vector Control of the DFAM
Let us consider a non-linear system MIMO where dynamic equation is described by the following expression

with: X = [x(n-1) ,...,x], x = [x1 ,...,xm ] and u = [u1 ,...,um ]t where x(j) is the jth derivative of x.
F(X) and G(X) are respectively a matrix and a vector of nonlinear functions.
The problem of the adaptive fuzzy control based on the inverse identification consists in the elaboration of a set of independent controllers (control with decentralized structure). For that, we decompose the system given by equation (24) to m subsystems; each subsystem is controlled locally by a control station which exceeds only to local information of the subsystem.
In the adaptive fuzzy control based on the inverse identification, ui is approximated by a one order Sugeno fuzzy system.

A fuzzy rule of the knowledge base of the function fi (X;θi ) has the following form:
where
1 ≤ l(q,j) ≤ m(q,j); k = 1,..., M, m(q, j) is the number of fuzzy sets associated to the input xiq of the fuzzy system, and M is the total number of the fuzzy rules;
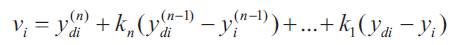
yi and yid are respectively output and desired reference. Coefficients ki are selected so that the polynom
Sn +knSn-1 +...+k1 is a Hurwitz polynom.
The vector θi encompass all the parameters of the fuzzy system; i.e., parameters of the membership functions and those of the conclusions.
The final output of the fuzzy system is given by,
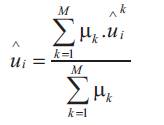
where µk represents the activation degree of the rule Rk . It is given by,
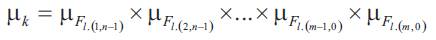
For a given input X, the fuzzy system is trained by a teaching algorithm in order to minimize the instantaneous error at the input of subsystem i. This error is defined by,

The adaptation law is given by the following equation,
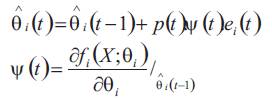
Where p(t) is the gain of the estimation algorithm. In the modified gradient method, the gain p(t) is chosen variable, and is given by the following equation:
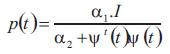
By using the equilibrium equation between the motor and resistive torques we can write:
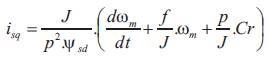
This equation can be put in the form:
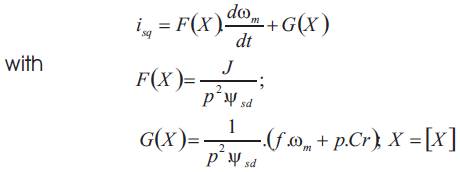
In order to be able to apply the adaptive fuzzy control based on the inverse identification, current Isq is approximated by a Sugeno fuzzy system of one order such as:
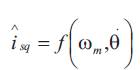
For the studied case, the fuzzy system has only one input which is the speed ωm; three membership functions are m assigned to this input.
The final input of the fuzzy system is given by:
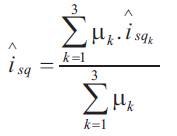
where 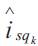 represents the consequence of the rule Rk . Its expression is given by:
represents the consequence of the rule Rk . Its expression is given by:
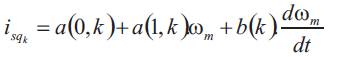
and µk represents the confidence degree of the rule Rk .
A consequence of the rule Rk of the fuzzy controller is given by:
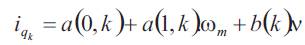
with
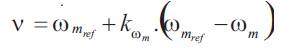
The desired current isqref is given by the following relation:

The vector of the parameters θ is estimated in order to minimize the following instantaneous error
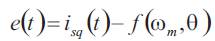
The control structure is given by figure (2)
An adaptive fuzzy logic control of the stator flux oriented control has been simulated [11]. The coefficient imposing the desired responses is Kωm = 2000. In the Figure 3 shows m the starting and the reference speed tracking performance of the DFIM (load torque application at t=0.5s, and speed reference changing at t=1s). A rapid response is obtained. Besides, it is very close to the desired reference.
The dynamic response of the speed and the electromagnetic torque with a change in the load torque show that the input reference is perfectly tracked by the speed and the introduced perturbation is immediately rejected by the control system.
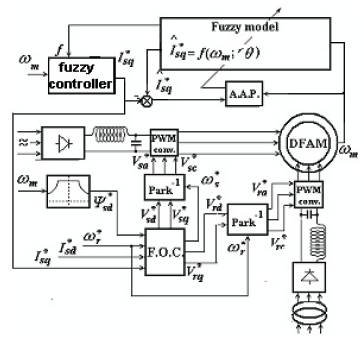
Figure 2. Structure of Speed Regulation by the Adaptive Fuzzy Control Method based on the Inverse Identification
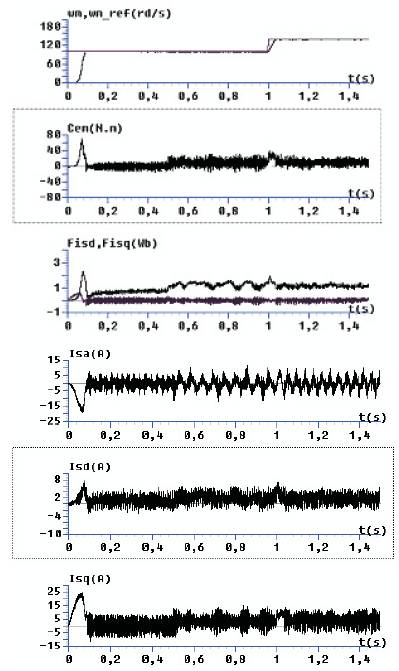
Figure 3. Load Torque Application at t=0.5s, and Speed Reference Changing at t=1s.
Moreover, it is clearly shown for stator flux responses that the decoupling is realised since the direct component of the stator flux converges to the reference (Ψsd)ref and its quadrature component to zero[12] .
Here Figure 4 shows the robustness quality of the proposed control scheme regarding the parametric variations of the machine. The dynamic behaviour of the speed is shown with a 75% rise of (rr ,rs ), and -25% of (lr ,ls and m) relative to the identified model parameters. The controller is not involved by these variations. Results encourage the implementation of this control.
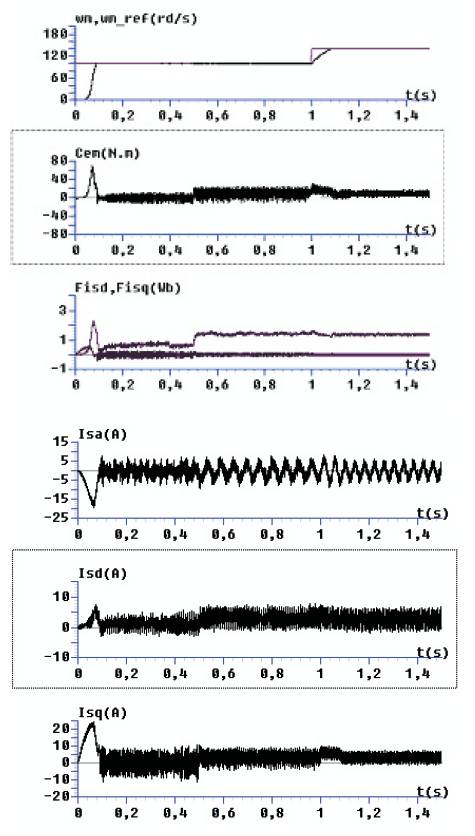
Figure 4. changing parameter effect (75% rise of (rr , rs ), and -25% of (lr , ls and m).
An indirect adaptive fuzzy logic control for the stator field oriented double fed asynchronous motor has been presented. With the proposed controller, successful and reliable operation of the machine is illustrated with the simulation results. The robustness quality of the proposed control appears clearly in the test results as we change machine parameters and especially under a load torque variation. However further study taking into account magnetic saturation of DFAM and inverter switching losses are necessary for a final evaluation of the proposed control scheme.
Moreover, this work can be improved by using multilevel inverter or matrix converter in the rotor circuit, and the genetic algorithms to optimize the different gains and parameters of the fuzzy systems. In addition, it is interesting to apply the combination of fuzzy logic and sliding mode controls in the commutation surface to ovoid the undesirable oscillations mainly the chattering phenomenon of the torque.
Machine of 1.5 kW, 220V, 12V.
rs =4.85, rr =3.805
ls =0.274H, lr =0.274H, m=0.258H,
J=0.031 kg.m2 ,
ƒ=0.008 N.m.s/rd,