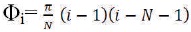
Pulse compression is important in many of the radar systems. It is a signal processing technique mainly used in radar and sonar to increase the range resolution and signal to noise ratio. It is used to overcome problems of a radar system, which requires a long pulse to achieve large radiated energy and a short pulse for Range resolution (Skolnik, 1981). The resolution is the ability of radar to differentiate targets that are closely placed together in range. In general, the short and long duration pulses are necessary for good range and velocity resolution in the radar, respectively because the long duration pulse that is transmitted is responsible for detection, and the bandwidth which is increased after modulation is responsible for the range resolution (Lewis, 1993; Lewis & Kretschmer, 1981).

Lewis (1993) has proposed that in this technique, the highest sidelobes are reduced to only one code element magnitude independent of the pulse compression ratio.

Lewis and Kretschmer (1981) have proposed a sliding window two sample subtractor technique to reduce sidelobes for polyphaser codes. Sidelobes in Barker code can be minimized with multiplicative mismatched filters (Sarkar & Fam, 2008). Sidelobe reduction in pulse compression radar can also be achieved with NLFM (Vizitiu, 2014).

Lee (2006) in the proposed technique improved the range-sidelobe reduction without increasing the system complexity. And also the technique is robust to the existing noise sources (Lee, 2006).

Kretschmer and Welch (2000) have proposed amplitude weighting technique for reduction of sidelobes in polyphase codes (Kretschmer & Welch, 2000). Zakeri, Zahabi, and Alighale (2012) have proposed some techniques to improve the signal to noise ration in polyphase codes. Lewis and Krestschmer (1982) have presented the variants of Frank code in their paper. P1 code which is derived from step frequency, Bolter matrix derived P2 code, and linear frequency derived P3 and P4 codes. The significant advantage of P1 and P2 codes over the Frank code and the P4 code over P3 is that they are tolerant to receiver band limitations (Lewis & Kretschmer, 1982). A new pulse compression technique was introduced that can reduce sidelobes significantly (Kumari, Rajarajeswari, & Krishna, 2005; Lee & Griffiths, 2004; Lee, 2006).

The codes that use any harmonically related phases based on a certain fundamental phase increment are called Polyphase codes. Different polyphaser codes are Frank, P1, P2, P3, P4. All these P1, P2, P3 and P4 codes are the modified versions of Frank code. The polyphase code does not have any restrictions in terms of length, i.e it does not have any fixed length, can be for any length of code. The other advantage of this P4 code is that it is more Doppler tolerant when compared to other polyphase codes. Here P4 code is used for thee valuation.

The phase sequence of P4 code is

(1)

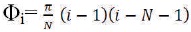
Equation (1) gives the phase sequence of P4 code and the performance characteristics that are considered here are Peak Sidelobe ratio (PSL ratio) and Signal to Noise Reduction (SNR) loss.

The peak side lobe ratio is calculated by

(2)

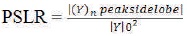
Equation (2) shows the performance calculation of P4 in terms of peak to sidelobe ratio by amplitude weighting for further reduction of sidelobes.

The proposed technique with Woo filter is shown in Figures 1 and 2. The block diagram (Figure 1) shows the Woo filter form 1, where the input signal has undergone one bit shift. The original signal and one bit shifted signal both are added together and given to the autocorrelation block which act as a matched filter. In Figure 2, the modified Woo filter is summation of the original signal and one bit shift of the original signal. The output of this matched filter is subjected to amplitude weighting. The signal that is subjected to weighting is cross correlated with the matched filter output.

Figure 1. Schematic Diagram of the Proposed Technique using Woo Filter Form 1

Figure 2. Schematic Diagram of the Proposed Technique using Modified Woo Filter Form 2

In this, the P4 code of length 1000 is considered for evaluation. In this technique, combination of the input P4 signal and one- bit shifted version of the input signal is applied to amplitude weighting technique using different weighting techniques. such as Hamming, Hanning and Blackman, etc. This produces a better PSLR ratio and SNR loss.

3.1 Woo Filter Form-1 Results

Table 1 shows the comparison of PSLR and SNR loss for different windowing techniques using Woo filter form I.

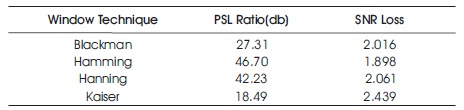
Table 1. Comparison of PSLR and SNR Loss for Different Windowing Techniques using Woo Filter Form 1

Figures 3 - 6 show that the PSLR and SNR loss is better for Hamming window compared to other windowing techniques.

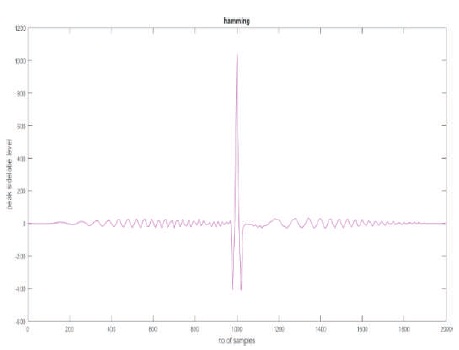
Figure 3. Sidelobe Level using Hamming Window

Figure 4. Sidelobe Level using Hanning Window

Figure 5. Sidelobe Level using Blackman Window

Figure 6. Sidelobe Level using Kaiser Window

3.2 Woo Filter Form-2 Results

Table 2 shows the comparison of PSLR and SNR loss for different windowing techniques using Woo filter form 2.

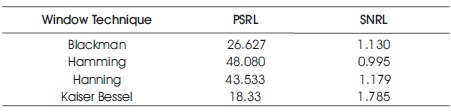
Table 2. Comparison of PSLR and SNR Loss for Different Windowing Techniques using Woo Filter Form 2

Figures 7 - 10 show that the PSLR and SNR loss is better for Hamming window compared to other windowing techniques.

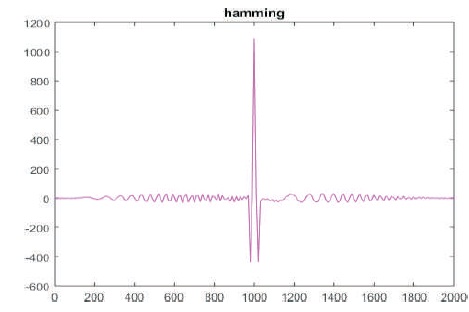
Figure 7. Sidelobe Level using Hamming Window

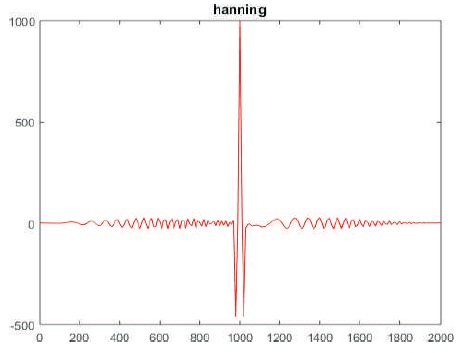
Figure 8. Sidelobe Level using Hanning Window

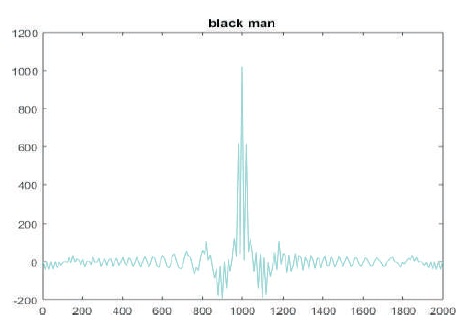
Figure 9. Sidelobe level using Blackman Window

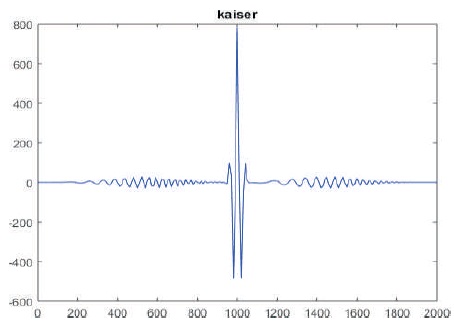
Figure 10. Sidelobe level using Kaiser Window

In this paper, the sidelobe reduction for polyphase codes is presented. In order to reduce the PSLR values further, weighting techniques are employed. Different windowing functions are studied and the performances of these windows for P4 code are presented. A novel technique Woo filter form 1 and form 2 is proposed and the performance characteristics such as PSLR and SNR loss has been calculated. The comparison results show that the Hamming filter provides better PSLR and SNR loss by using Woo filter form 2.