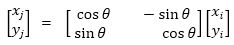
In this paper, the authors illustrate the design of the exponential function based on the conventional and scale free hyperbolic Coordinate Rotation Digital Computer (CORDIC) algorithm which are used in applications of the neural networks Very Large Scale Integrated circuit design. The CORDIC algorithm is introduced to design the function of the neural networks. The design of exponential function based on conventional and scale free hyperbolic CORDIC processor is coded in VHSIC (Very High Speed Integrated Circuit) hardware description language and their simulation and synthesis results are present in this paper. The Xilinx 13.1 software is used for the simulation and synthesis of code design.
Artificial Neural Networks (ANN) (Qian, 2006) are a high-complicated nonlinear dynamic system in function. The Artificial Neural Network is a method for learning knowledge. For example, the authors take the multilayer perception of an ANNs. These are arranged in layers and connected via interconnects. Each neuron from a previous layer feeds every neuron on the next layer with amplification. Neurons accumulate the sum of each of its inputs scaled by interconnect which is called synaptic weight to generate the net value, which is called the net function and the resultant output value of the neuron is measured by the activation function of the neuron. There are some difficulties in the implementation of parallel characteristics of ANNs (Haykins, n.d; Meyer-Bäse et al., 2003), which are used for parallel computation on Very Large Scale Integration (VLSI) of ANNs because of much more multiplication operations and activation functions operations. The digital implementations of neurons are either very complex or very simple. y=f(x)=1/1+e-x or hyperbolic tangent function y= f(x)=tan(x), which smoothen the transition between excitation and inhibition thereby improving neural response. The CORDIC algorithm (Volder, 1959, 2000; Walther, 1971, 2000; Hu & Naganathan, 1993) has various applications like digital filter implementation, FFTs, DCTs (Volder, 1959, 2000; Walther, 1971, 2000; Hu & Naganathan, 1993). It can be employed to calculate many transcendental algebraic functions, which can be used in neural networks, VLSI design, such as multiplication, division, hyperbolic, and trigonometric function. There are several advancements in the CORDIC algorithm for saving the hardware area and reduction in the number of iterations, delay and compensate on the scale factor in which one improved CORDIC algorithm is a scale free CORDIC algorithm.
In this paper, the conventional and generalized CORDIC algorithms are introduced in section 2. In section 3, the authors discuss about the hyperbolic CORDIC Processor. In section 4, the authors explain the design steps of scale free hyperbolic CORDIC processor. Section 5 gives the realization of the very simple function = f(x)=1/1+e-x, and it also analyzes about the area complexity issues, latency, range of convergence, and relative error plot of the circuit design.
The CORDIC algorithm means co-ordinate rotational digital computer which was invented by a great scientist Jack E. Volder. A planar rotation is a good explanation of the CORDIC algorithm as shown in Figure 1. Suppose that converting a vector (xi, yi) into a new vector (xj, yj) is rotated by an angle θ, it is defined as,
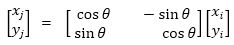
Figure 1. Planar Rotation of a Vector
The angle θ can be decomposed in several small angles using an iterative process. An iterative process is called micro-rotation. An iterative process is defined by the following equation.
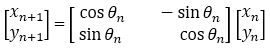
Here n= number of iterations. Equation (2) can be modified by taking cosq factors outside from the bracket.
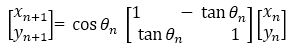
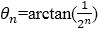
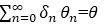
where δ ={+1, -1}
This results in the following equation for tanθn.
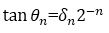
Combining equations (3) and (6), the following results are obtained.
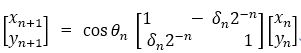
The algorithm has been reduced to a few simple shifts and additions except cosθn coefficient. The term cosθn can be omitted by pre-computing the final results. First of all, the coefficient is rewritten.
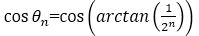
And then, for all values of 'n' from 0 to ∞ and multiplying the results, we can get equation (8), which will refer as scale factor K.
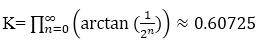
where K is constant for all initial vectors and for all values of the rotation angle, because the coefficient K is pre-computed and taken into the account at a later stage as a scale factor. Equation (7) may be rewritten as,
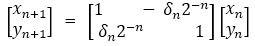
or
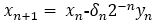
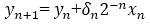
Here a new variable term called ‘z’ is introduced. z represents the rest of the rotation angle θ.
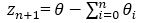
Using equations (4) and (13), the final equation of the angle θ is mentioned below.
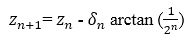
Thus the basic CORDIC equations are,
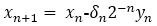
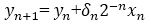
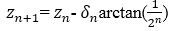
There are two modes in CORDIC algorithm, one is rotation mode and another one is vectoring mode. In vectoring mode, initial vector (xn, yn) are rotated until yn becomes closer to zero, while in rotation mode, initial vector (xn, yn) are rotated until zn approaches to zero.
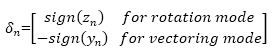
Hence, in rotation mode,
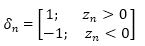
And in vectoring mode,
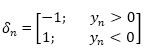
So, we can say that CORDIC algorithm is useful for the evaluation of elementary functions due to its simple add-shift operation property. So the CORDIC processor is used in different engineering fields due to its simple add-shift property.
After few years, there are some needs of improvements in the CORDIC algorithm. So Walther had introduced a new generalized and unified CORDIC algorithm. This unified algorithm is useful to execute rotations in different coordinate systems like circular, hyperbolic, and linear coordinate systems. For defining these three coordinate system, one variable m is introduced in the unified CORDIC equation having three different values. The generalized CORDIC is formulated as follows:
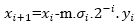
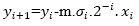
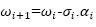
where m=1 circular, 0 linear, -1 hyperbolic.

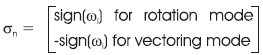
The trigonometric, hyperbolic functions, and multiplication are computed using a single chip CORDIC processor and its rotational mode is the rotation and trajectories are circular, hyperbolic, and linear, respectively. If mode is set in vectoring then we can calculate their inverse functions using relevant coordinate system.
An unified CORDIC algorithm in hyperbolic coordinate system of equations are formulated as given below:
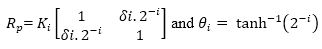
For hyperbolic CORDIC processor, the iteration number i=4, 13, 40 are executed twice for improving the convergence range. The scale factor K value is 1.207583 in hyperbolic CORDIC processor. The Range of Convergence (RoC) of angle is -1.1182 to 1.1182 in the conventional CORDIC hyperbolic processor. The limit of convergence has restriction from the CORDIC processor at certain range of target angle. For the enhancement of target angle range, there is some need of improvement of conventional CORDIC algorithm. A new idea is introduced for the CORDIC algorithm. This is a scale free CORDIC algorithm for increasing the range of convergence. Scale factor is completely eliminated in this new improved CORDIC algorithm. Scale free CORDIC algorithm involves few steps which are mentioned below.
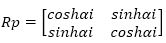
The Taylor series expansion of the hyperbolic functions are given by,
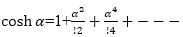
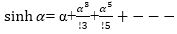
The need of accuracy, range of convergence, and hardware complexity according the desired application of the users decide the selection of the order of the Taylor series in the scale free CORDIC algorithm. The calculated and approximated value of sinh and cosh is very closer for the third order Taylor series in the range of [0,π/4]. The percentage error in sinh and cosh values for third order approximation is optimum as compared to the second order and fourth order Taylor series approximation. So the authors select the third order Taylor series for the rotation matrix in scale free hyperbolic CORDIC processor. Thus the rotation matrix of CORDIC hyperbolic mode by using Taylor series is mentioned below.
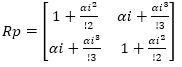
The suggested algorithm used third order expansion and approximate factorial 3 to 22, so the rotation matrix becomes as:
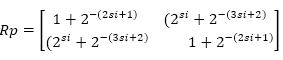
These equations give the next coordinate values xi+1, yi+1. These equations depend on shift index values, which are calculated using the N word length and M, which is the location of the most significant bit.
In conventional CORDIC, the elementary angles are predefined and stored in a Read Only Memory (ROM), the micro-rotation corresponding to all the elementary angles are performed either clockwise and anticlockwise, and each elementary angle is used only one time. But in scale free CORDIC Processor (Maharatna et al., 2004, 2005) the micro-rotations are rotated in only one direction, and in scale free CORDIC processor, there are multiple iterations. For storing elementary angles in scale free CORDIC processor (Meher et al., 2009; Jaime et al., 2010; Aggarwal & Khare, 2011), the elementary angles are redefined as:
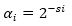
where si is the number of shifts for ith iteration.
The most–significant one bit location refers to the bit position of the leading one in an input string of bits starting from Most Significant Bit (MSB). The Multiple System Operator-Location Identifier (MSO-LI) generates an n-bit output for a 2n bit input string. It is used for finding the shift index.
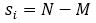
Here, N is the word length of the input data and M is the location of the Most Significant Bit (one) in N input word length. The largest elementary angle depends on the order of approximation of Taylor series. The basic shift and the largest elementary angle for a third order of approximation is to be:
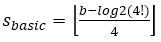

where b is the word-length. For 16 bit word length, sbasic =[2.854]. Depending upon the desired accuracy, one can either select sbasic =2 or sbasic =3. Any rotation angle θ is expressed as:
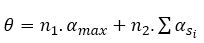
where si ≥ sbasic and n=n1 +n2, n is the total number of basic iterations ('n' is a constant). For third order Taylor series, the optimum value of iterations are seven. For designing of scale free CORDIC processor and micro-rotation sequence generator the input: angle is to be rotated θi. The most significant one’s bit location is represented by MSO-LI (Location Identifier). If ML=15 then α =0.25 radians shift si=2, θi+1=θi-α. If ML is other than 15 then shift si=16-ML and θi+1=θi with θi [ML]='0'.
Table 1 shows the bit representation of elementary angles in decimal and hexadecimal according to the corresponding shifts. Figure 2 shows the design of coordinate calculation unit for hyperbolic scale free CORDIC processor (Aggarwal, Meher, & Khare, 2013). The input coordinates are xi, yi, and output coordinates are xi+1, yi+1. The coordinates calculation unit is designed using shift registers and adders.
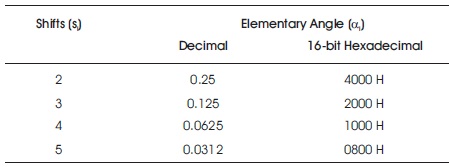
Table 1. Angles and Respective Shifts
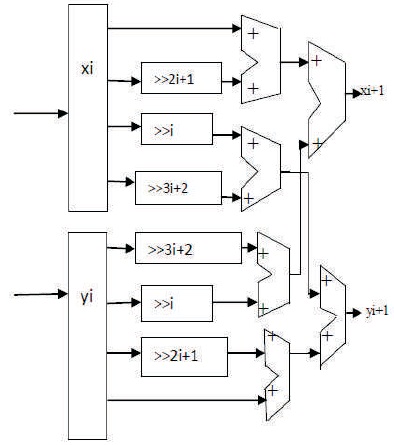
Figure 2. Design of Coordinate Calculation Unit
The shift index si calculation unit is shown in Figure 3. For obtaining the next shift values in this unit, the authors use shift registers and adders. In scale free CORDIC processor, the percentage error for the sinh and cosh is indistinguishable for the range (0,π/4). So the maximum angle of rotation directed by micro-rotation sequence generation lies in the range (0,π/4), further for range improvement uses octant symmetry.
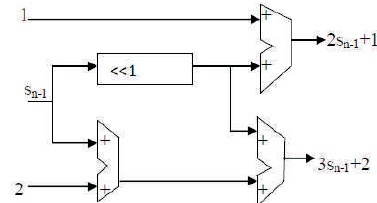
Figure 3. Shift Index s Calculation Unit
The hyperbolic CORDIC processors and some exponential functions designed using the hyperbolic CORDIC processor are mentioned as follows. The hyperbolic CORDIC processor is designed using conventional CORDIC algorithms and scale free CORDIC algorithm. These designs are coded by using Xilinx Integrated Systhesis Environment (ISE) 13.1 to be mapped in to Xilinx Spartan -3 (xc3s400-5pq208) devices. The few exponential functions are mentioned below.
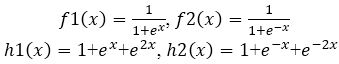
The scale free hyperbolic CORDIC processor has higher frequency than conventional hyperbolic CORDIC processor. The number of iterations, delay, and gate count are less for the scale free hyperbolic CORDIC processor as compared to the conventional hyperbolic CORDIC Processor. Table 2 shows the different parameter values comparison for the scale free and conventional hyperbolic CORDIC processor.
From Table 2, the authors observed that the scale free CORDIC processor consumes less area and reduces the propagation delay and number of iterations. Table 3 shows the percentage error calculation for different exponent functions. From Figure 4, it is observed that the scale free CORDIC processor based exponential function values which are coded in Xilinx 13.1 software are closer to the exponential function values which are obtained through Matlab as compared to the conventional CORDIC processor based exponential functions.
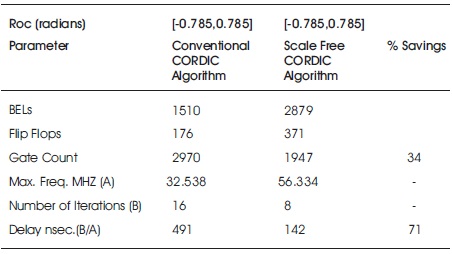
Table 2. Complexity Comparison: Hyperbolic CORDIC Processor
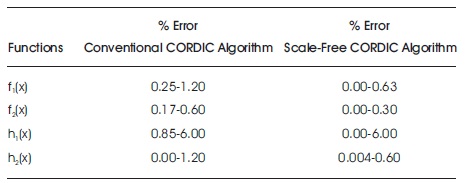
Table 3. % Error Calculation: Different Exponent Functions
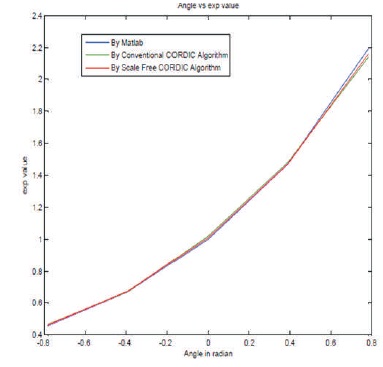
Figure 4. Graph of Exponential Function
Figure 5 illustrates the relative error plot of the scale free CORDIC processor based exponential functions and conventional CORDIC processor based exponential functions. The relative error of the scale free CORDIC processor based exponential functions varies from -1 to 1, but the relative error of conventional CORDIC processor based exponential functions varies from -4 to 2.5. This shows that the scale free CORDIC processor based design for calculation of the exponential function are useful for the neural network which is prominent as compared to the conventional CORDIC processor based design.
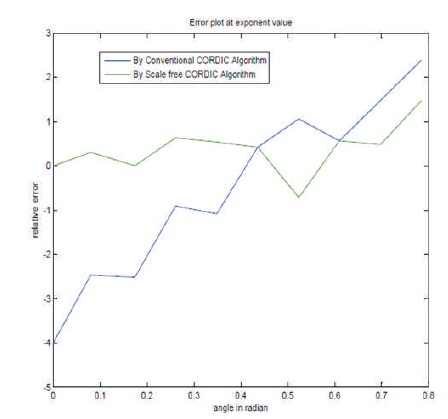
Figure 5. Relative Error Plot at Exponent Value
The scale free hyperbolic CORDIC processor has low value of the gate count and it requires the lesser number of iteration. The scale free hyperbolic CORDIC processor has a small delay as compared to the conventional hyperbolic CORDIC processor. The percentage error for scale free CORDIC processor based design for evaluating the different exponential function is also less. The scale free CORDIC hyperbolic CORDIC architecture proves to be a hardware efficient option for VLSI implementation of the activation functions and Gaussian potential functions in the neural networks. The word-length of the processor is increased upto 32 bit, 64 bit for enhancing the efficiency. The scale free CORDIC algorithm has unidirectional iterations and requires only 8 iterations for the transcendental function calculations.