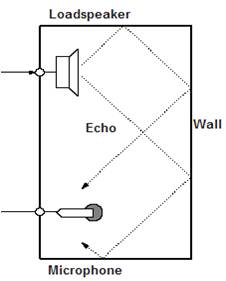
Figure 1. Echo in microphone
The problem of echo is foremost in today's telecommunication systems. It generally occurs in full duplex mode means when source and sink both communicate at a time. Hands-free loudspeaker telephone is a common example. It can also be seen in case of speech. In this situation, the signal which is received is output through the telephone loudspeaker, the original signal is reverberated because of unwanted signal called echo. This effect is time delayed and attenuated original signal to the user. Because of this echo, the signal interference is caused to both user side which causes reduction in quality of signal. This interference distracts both users. Therefore, the more important task is cancellation of this echo to get signal without degradation in signal quality. This paper focuses on the use of adaptive filter techniques to reduce this unwanted echo, which results in increasing communication quality. A class of filters that iteratively alter its parameters is adaptive filter which is used in order to minimize a function of the difference between a desired target output and their own output. Comparison analysis of all adaptive filter algorithms is done for echo cancellation in this paper.
Echo is defined as a reflection of sound in audio signal processing and acoustics which is arriving at the listener with some delay after the direct sound. In the propagation medium, its a wave that has been reflected by a discontinuity, and returns back with sufficient delay and magnitude [13]. When an audio signal is reverberated in a real environment, acoustic echo occurs, which results in the original intended signal along with attenuated and delay time. Figure 1 shows the occurrence of echo in microphone through wall. When the signal is received by a system, the output of the signal comes out at the environment through loudspeaker. The signal returns back into the system via microphone input and is reverberated in the environment. The Solution to cancel such an echo is Adaptive Filter.

Figure 1. Echo in microphone
In order to achieve an optimal desired output, adaptive filters also known as dynamic filters are used which iteratively alter their characteristics. Digital filters that have self optimizing characteristics are also known as adaptive filter. In many Digital Signal Processing (DSP) applications, adaptive filtering is gaining momentum from last few decades and also in current technical advancements such as noise filtering, voice prediction and system identification. Digital Signal Processing (DSP) plays a major role [14]. Standard DSP techniques alone are not enough to solve such problems quickly with acceptable results.
Different adaptive filtering techniques must be implemented for exact solutions. To model the relationship between two signals in an iterative manner in real time an adaptive filter is used. Adaptive filters are defined either as a set of program instructions device such as a microprocessor or DSP chips running on an arithmetical processing [1]. Following are the four aspects of adaptive filter:
Figure 2 shows the block diagram of adaptive filter. Here the input signal Xn is input to the filter and the received signal is then compared with the desired signal. The difference in desired signal and occurred signal gives error signal in which adaptive algorithm is applied for perfect echo cancellation [9].
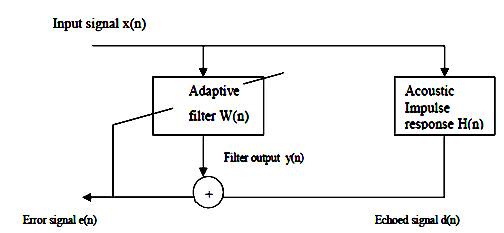
Figure 2. Block Diagram of Adaptive Filter
Thus, this paper is further organized as: Section 2 is Adaptive filter algorithm. Section 3 shows mathematical calculation for all algorithms. Section 4 represents simulation results and conclusion is given in the last section.
Various types of adaptive filter algorithms are used for noise cancellation as shown in Figure 3. Choices of these algorithms depend on the types of application used. These applications include removal of interference, noise cancellation systems, acoustic echo cancellation systems [6], etc.
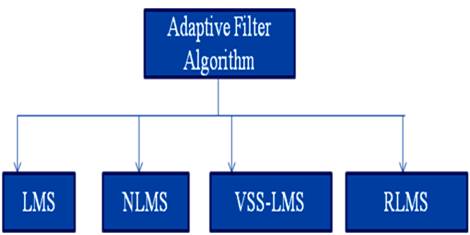
Figure 3. Classification of Adaptive Filter Algorithm
One of the most popular algorithm used in adaptive filter is LMS Algorithm. No prior knowledge and simplicity are the two major advantages of LMS algorithm [10]. Here, the update function is obtained by the multiplication of the current value of the error signal with the step size and input signal and it does not depend on any other previous value. Slow convergence is the main disadvantage of LMS algorithm due to the step size restriction. Step size of the input signals depends on the eigen value of the auto correlation matrix [2]. Several other methods have been used to speed up the convergence of the LMS algorithm with increased complexity.
The normalized form of the LMS algorithm is referred to as normalized least mean square algorithm. Difficulty in selection of step size in LMS algorithm is eliminated in NLMS algorithm. Norm function in denominator of weight update function that results in reduction of noise is the main advantage of NLMS algorithm [3]. Also it has faster rate of convergence than LMS. Complexity in computation is more than LMS which is the main disadvantage with this algorithm.
Both the LMS and the NLMS algorithms have a fixed step size value for every tap weight in each iteration. In the Variable Step Size Normalized Least Mean Square (VSS-NLMS) algorithm, there is step size for each iteration. One of the major advantages of variable step size NLMS adaptive filters developed are fast convergence rate with a low excess mean square error. Here when the estimated error is larger, the step size is larger and vice versa. The criteria for selecting the variable step size are shown in [4]. The estimated system noise power and the mean square error are used to control the step size. Low steady state error and good tracking capability are the other advantages of VSSNLMS.
Cost minimization is the major advantage attempted by this algorithm which is the drawback of all the above three discussed techniques. The Recursive Least Squares (RLS) adaptive is an algorithm which recursively finds the coefficient used to minimize a weighted linear least squares cost function relating to the input signals [5]. RLS can be used to perform all the functions performed by adaptive filter.
Figure 4 shows the processing steps for the echo cancellation using different adaptive filter algorithm.
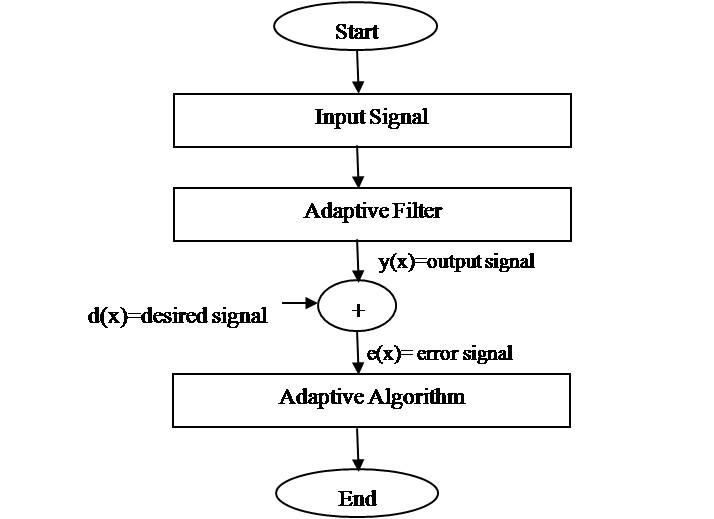
Figure 4. Processing Steps for Echo cancellation
Filter size is considered first with step size and iteration. Then algorithm is applied.
Implementation steps are given below:
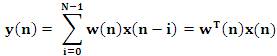
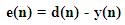
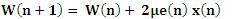
LMS algorithm requires 2N addition and 2N+1 multiplication for each iteration. Here, the step size is originally considered for a deterministic gradient.
NLMS bypasses the issue of LMS by selecting a different value of step size μ(n), for each iteration of the algorithm [7]. All implementation is same as LMS for NLMS. Only one difference is, the step size and the total expected energy of the instantaneous values of the coefficients of the input vector x(n) is inversely proportional to each other.
Implementation steps are given below:
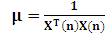
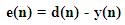
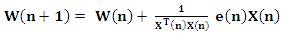
Here 3N+1 multiplication is required.
In LMS and the NLMS algorithms, both have a fixed step size value in each direction for every tap weight. In the Variable Step Size Normalized Least Mean Square (VSSNLMS) algorithm, the step size for each iteration is expressed as a vector [(μ(n)] [11].
Implementation steps are given below:
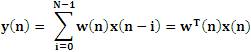
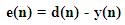
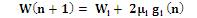
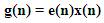
The step size is μ where each element of the vector μ(n) value corresponding to an element of the filter tap weight vector [w(n)]. 5N+1 multiplication is required.
The Recursive Least Squares (RLS) adaptive is an algorithm which recursively finds the filter coefficients that minimize a weighted linear least squares cost function relating to the input signals.
Implementation steps are given below:
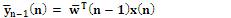
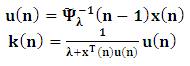
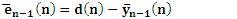
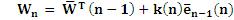
RLS algorithm requires 4N2 multiplication.
The following figures shows the input signal, echoed signal, adaptive filter output signal, estimation Error by echo cancellation plots.
The results in Figure 5 have been obtained for 10500 iterations with filter length of 100. It shows that as the algorithm progresses the value of cost function decreases which in return corresponds to the LMS filters impulse response that converges to the actual impulse response. More accurate desired signal is emulated results in more effective cancellation of echo signal. The results have been shown only for no of iterations=10500 and filter order 100.
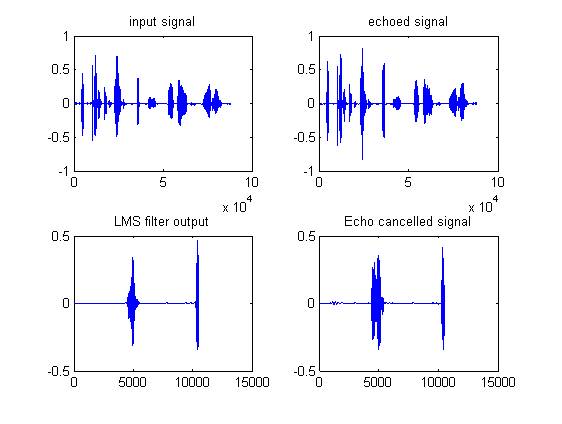
Figure 5. Plots of echo cancellation using LMS
The curve in Figure 6 shows the results for the Normalized LMS algorithm. NLMS result shows that it performs better than LMS. NLMS is superior than LMS in case of everything i.e. step size, convergence, cost etc. The adaptive algorithm also performs the function that provides high ERLE (Echo Return Loss Enhancement), real time operation and fastest convergence [8]. NLMS has higher ERLE, so it works as a better algorithm for echo cancellation application.
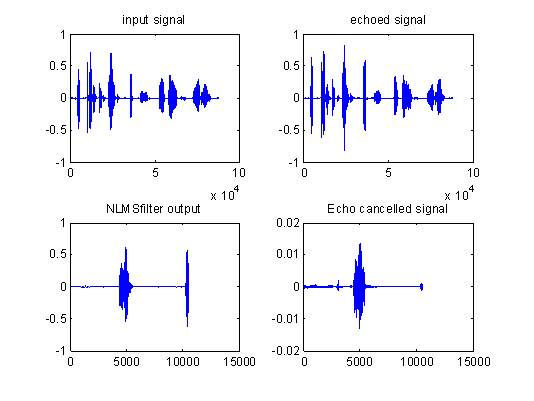
Figure 6. Plots for echo cancellation using NLMS
Figure 7 shows the plot for VSS-NLMS. Both LMS and NLMS are used for fixed step size. Here the authors have taken variable step size for both lower and upper. This algorithm performs better in all cases with respect to rest both methods. High Convergence rate, less complexity are the main advantages of VSS-NLMS.
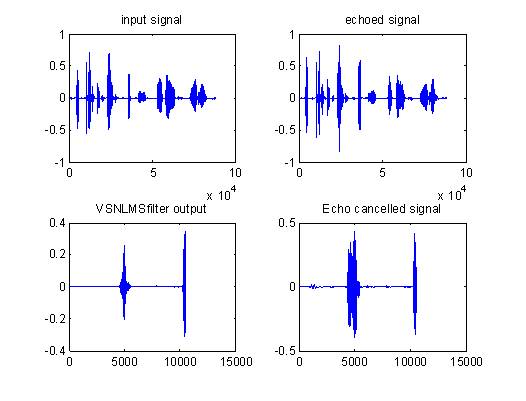
Figure 7. Plots for echo cancellation using VSS- NLMS
Figure 8 shows the plot for RLS algorithm. Convergence rate is same as LMS and NLMS. The only difference with its advantage is that it is very cheap. Step size of 0.007 has been taken with number of iterations = 10500 and filter order = 100.
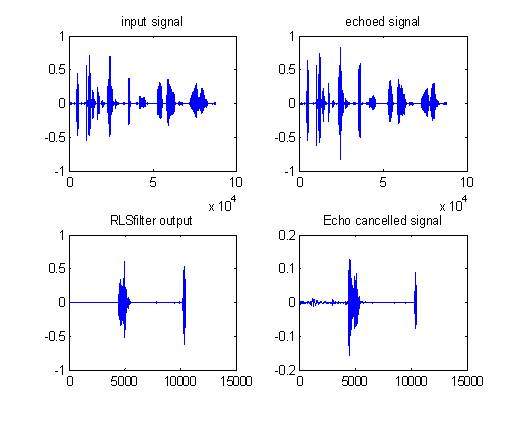
Figure 8. Plots for echo cancellation using RLS
One specialized branch of DSP is adaptive Digital which deals with adaptive filters and system design. Number of adaptive algorithms are available in literature and each algorithm has its own properties, with the same aim of high convergence at least cost and lesser complexity. LMS, NLMS, VSS-NLMS, RLS adaptive algorithms have been discussed in this paper. However convergence and tracking of the NLMS is more than LMS algorithm. NLMS is simple to implement and computationally efficient, shows very good attenuation and variable step size allows stable performance with non-stationary signals. This was the obvious choice for real time implementation. RLS algorithm has the greatest attenuation of any algorithm studied, and converges much faster than the LMS algorithm. VSS-NLMS performs best if variable step size has been used. Hence, it is required to make an adaptive algorithm with less computational complexity, less steady state and more stability along with good converge and tracking capability.