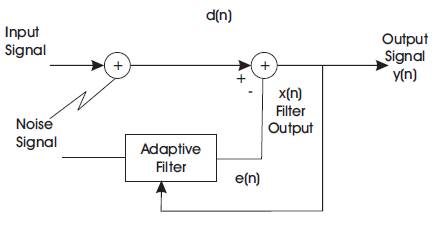
Figure 1. Basic Adaptive Filtering
In this paper, a novel approach of noise cancellation algorithm using Parallel Normalized Filtered x-LMS (P-NFxLMS) is proposed. The degraded audio signal quality can be improved by using adaptive filters. In general, Least Mean Square (LMS) adaptive filtering algorithms are used to recover corrupted signal. The implementation of LMS algorithm is simple. LMS algorithm exhibits degraded performance if the desired signal has large power fluctuations. The Normalized Fx LMS is also computationally simple and improves the performance of LMS algorithm. In this paper, an algorithm is proposed to decompose a long adaptive filter into multiple sub-filters with lower order, and are implemented in parallel to increase the convergence speed. Finally, the proposed Parallel Normalized Filtered x-LMS (P-NFxLMS) algorithm yields faster convergence with minimum Mean Square Error.
The aim of any filter is to retrieve the required information from noisy data. In general, a filter is designed in advance with the knowledge of parameters of signal and noise. If noise parameters are not known in prior or changing continuously, the filter must update the coefficients. This can be achieved using adaptive filtering algorithms. Adaptive filters are iteratively modifying their qualities to accomplish an ideal performance. An Adaptive filter algorithmically adjusts its parameters to minimize the error. Figure 1 shows the solution for adaptive noise cancellation using adaptive filtering technique. The input signal d(n) is the summation of input and noise. Adaptive filter produces its output x(n) by taking input as noise. The error signal which is e (n) =d (n)-x (n), is generated and iteratively adjusted in order to produce the required performance of the system [9].

Figure 1. Basic Adaptive Filtering
One of the main applications of adaptive filtering is noise cancellation of an audio signal called as ANC is used in time-varying signals and systems. In digital signal processing, the corrupted signal is recovered effectively using ANC scheme [1], [2], [11], [10].
To improve the tracking ability and convergence speed of a corrupted signal, many LMS Algorithms have been proposed. All these algorithms provide better performance compared to basic LMS Algorithms including NDLMS, Fx- LMS, and NFx-LMS algorithms.
This paper analyzes the above algorithms and a new approach named Parallel normalized filter x-LMS (PNFxLMS) algorithm is proposed. In this algorithm, a long adaptive filter can be decomposed into multiple lower order sub-filters, the error signal of each sub filter is independent [3]-[5].
This shows the technique of parallelism, hence convergence speed can be increased with minimum Mean Square Error [6].
LMS algorithm is one of the popular adaptive filtering algorithms used in adaptive filters as it is simple, ease of realization and less mathematical complexity [9]. In the LMS algorithm, the update of weight equation and error signal equation are given below.
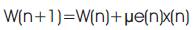
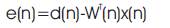
where, n is the time index, W(n) indicates L×1 vector, L is the Adaptive filter length, and μ is the Step size parameter.
An approximate condition for the convergence is: 0 < μ < 2/(LSmax ),
where Smax is the power spectral density maximum value.
The major drawback of the LMS algorithm is that, as the desired signal power increases, Mean Square Error (MSE) also increases linearly. This tends to reduced performance if the desired signal has large power variations [14] .
A Normalized Difference LMS (NDLMS) algorithm is used when the desired signal has large power fluctuations, which is a major disadvantage of LMS algorithm.
In this algorithm, the reference input and error output are substituted with difference reference input Δx(n) and difference output to update the weights of adaptive filter.
The weight update equation and error signal equation are given by,
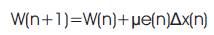
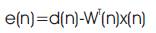
where, n is the time index, W(n) indicates L×1 vector, L is the Adaptive filter length, and μ is the Step size parameter.
The error produced in NDLMS algorithm is very small compared to LMS and NLMS methods. The adaptive noise canceller steady state performance is improved by using NDLMS algorithm [15].
This algorithm is good for performance and computational cost, but the major disadvantage of this algorithm is selection of step size μ. If the step size is small, it converges slowly with small misadjustments. On the other side, a large step size yields to faster convergence with a better tracking capabilities, with more misadjustments.
FxLMS algorithm is a gradient based algorithm. In this the reference signal x(n) is filtered and applied to LMS adaptive algorithm [12], [13]. The block diagram of FxLMS algorithm is illustrated in Figure 2:
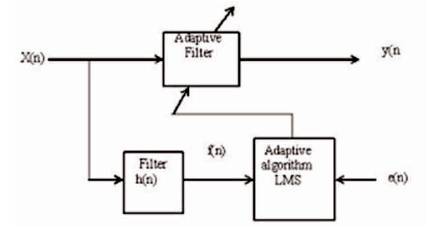
Figure 2. Block Diagram of FxLMS Algorithm
The ANC system based on FxLMS algorithm consists of two blocks, Adaptive filter and FxLMS based algorithm. The control signal y(n) is the output of adaptive filter and it is given by[8],
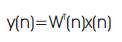
Here,
W(n) is L×1 adaptive weight vector with filter parameters W0 , W1 ,….., WL-1 .
and it is given as,
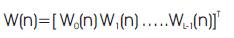
The reference vector x(n) is given as,
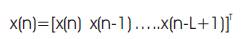
Using above equations, FxLMS based adaptive filter produces an output y(n) depending on noise e(n). The weights of algorithm are given by,
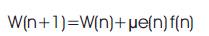
Here μ is a step size parameter and it is a scalar. f(n) is the filter response.
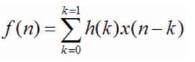
Where h(k) is impulse response of a filter at time index 'k'.
The major problem with FxLMS algorithm is slow convergence rate if the numbers of weights are increasing.
To overcome this problem and to enhance the filter performance, Normalized FxLMS algorithm is used [7], [12].
Normalized FxLMS algorithm is a modified version of FxLMS algorithm which uses the concept of Normalized LMS. In this algorithm, the step size μ value is chosen based on current input. Hence, NFxLMS algorithm shows better stability compared with FxLMS algorithm.
The Normalized FxLMS algorithm, updates the co-efficients using the following equation.
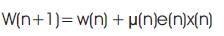
where
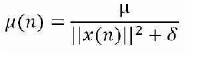
δ is small positive number added to avoid division by zero.
The main advantage of this algorithm is that the computational complexity is less. But, its convergence speed is still less.
In this paper, a new method is considered, a parallel Normalized Filtered x LMS algorithm. This algorithm uses a way to overcome the effect of slow convergence of long adaptive filter. This can be achieved by dividing a long filter into multiple sub filters and arranging them in parallel structure [8] [11]. NFxLMS algorithm is applied to update the weights of these sub filters.
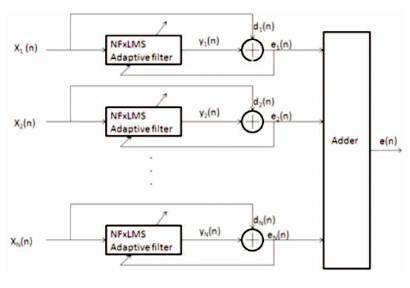
Figure 3. Block Diagram of Parallel NFxLMS Algorithm
The input signal is applied to all sub filters which are connected in parallel. These sub filters updates the weights using NFxLMS algorithm, where the error signal is independent of each other.
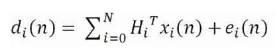
where Hi is the system function of ith adaptive sub filter. The signal xi is input signal. The error signal of sub filter is given by
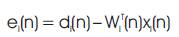
where Wi(n) is the weights of filter. The adaptive sub filter output is given by,
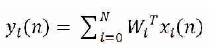
where i is number of iterations and i=1,2,3….N.
The weight update equation of each sub filter is
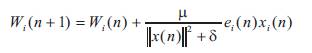
In this section the simulation results are described using MatLab to observe the performance of the proposed algorithm compared with the LMS algorithm. The desired signal d(n) is shown in Figure 4 is sampled and this signal is corrupted by random noise and it is shown in Figure 5 and the signal is given as an input to adaptive filter. The mean square error of the proposed algorithm with the comparision of LMS algorithm is shown in Figure 6. From Figure 6, it is clear that the proposed algorithm has minimum MSE with LMS algorithm.
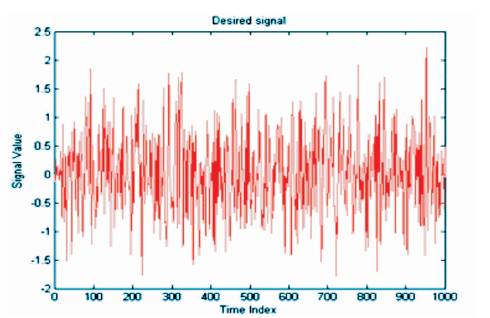
Figure 4. Desired Signal
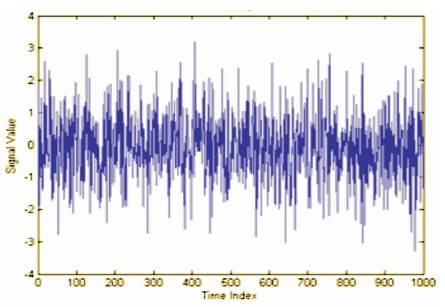
Figure 5. Random Noise Signal
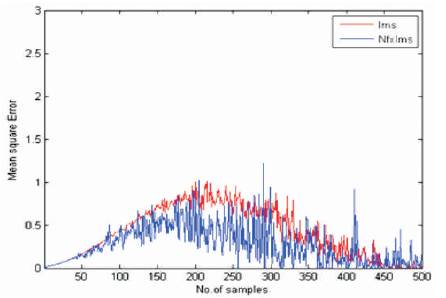
Figure 6. Comparison of MSE
The average MSE of LMS algorithm and P-NFxLMS algorithm are calculated using MATLAB and is shown in Table 1.

Table 1. Comparison of Average MSE
The table shows that P-NFxLMS algorithm has lower average MSE compared to LMS algorithm.
In this paper, a new Parallel Normalized Filtered x LMS algorithm is proposed to remove noise from the given signal. The advantages of Normalised Filtered x LMS Algorithm are improved by overcoming the convergence speed by decomposing the long adaptive filter into sub filters. A random signal is generated and applied to the above mentioned algorithm and processed for MSE and convergence speed.
The experimental results show that the proposed algorithm produces less MSE with fast converges rate and hence suitable for non stationary environment. Thus the theory and results show that the proposed algorithm is a hopeful method for noise cancellation. In this paper, a long adaptive filter is decomposed into multiple sub-filters with lower order, and is implemented in parallel to increase the convergence speed. Finally, the proposed Parallel Normalized Filtered x-LMS (P-NFxLMS) algorithm yields faster convergence speed with minimum Mean Square Error.