
Electrocardiogram (ECG) is a graphical illustration of the cardiac cycle as produced by an electrocardiograph. ECG recordings are indispensable when it comes to monitoring critical cardiac patients, astronauts etc. However, this around-the-clock surveillance results in voluminous ECG data, which becomes difficult to handle. Thus, the basic requisities of minimal usage of data storage space and speedy transmission over channels in tele-medicine fostered research in the field of ECG Data Compression. So far numerous techniques under Direct Data methods of compression like Turning Point (TP), Amplitude Zone Time Epoch Coding (AZTEC), Coordinate Reduction Time Encoding System (CORTES), Scan Along Polygonal Approximation (SAPA), Fan etc. have served the purpose fairly. This work tends to amalgamate the TP and modified AZTEC techniques, providing an efficient hybrid algorithm for compression.
Electrocardiography is a canonical procedure in these days, primarily because of an incessant growth in the number of heart patients. Since, modern day health facilities solely rely on software to handle cardiologic data of patients, a need is felt to satisfy the primary requirements of minimal storage space for data and its rapid transmission. With a variety of compression algorithms developed so far, we have achieved it to quite an extent but still there is scope for improvement.
For a compression algorithm to be competent in every aspect it should satisfy the three R's (i) Represent (ii) Retain and (iii) Reconstruct. By 'Representation' we mean that the algorithm must be equipped to compress long continuous ECG signals using few samples [5]. 'Retaining' pertains to the fact that the compressed data must retain the basic diagnostic information about the patient [10] and 'Reconstruction' here, implies that the algorithm must reproduce the original data from the compressed file with negligible loss. Most compression algorithms live up to the first two requirements but lag when it comes to data reconstruction. We use evaluation measures like Compression Ratio (CR) [2, 9] and Percent Root Mean Square Difference (PRD) [3]to estimate the genuineness of a particular algorithm. However, these are not the only testing parameters.
A very wide range of compression algorithms are available today. Wavelets, Parameter extraction, DDC all have played a vital role in the field of ECG compression. DDC or Direct Data Compression Technique alone has about eight to ten methods enlisted under it [3]. To name a popular few we have Turning Point (TP), Amplitude Zone Time Epoch Coding (AZTEC), modified AZTEC, Coordinate Reduction Time Encoding System (CORTES), Scan Along Polygonal Approximation (SAPA) [7], Fan [8] etc. These time domain techniques have not only provided good processing speed but also high compression ratios. Compression ratios as high as 10:1 have been obtained.
So far these techniques, when individually implemented have undoubtedly performed well but lately, intra-domain hybrids have gained grounds. The reason being that hybrids not only amalgamate but also incorporate the best features of the fundamental algorithms. The CORTES is one such concoction which successfully mixes the TP and AZTEC algorithms. It uses the high compression ratio of the AZTEC technique and at the same time claims high accuracy of the TP method. The current paper deals with a hybrid of TP and modified AZTEC technique. The Modified AZTEC technique is different from AZTEC in the respect that it is self- adaptive in nature and has a variable threshold unlike the AZTEC [4]. These techniques have been intertwined on the lines of CORTES algorithm and certain enhancements have been incorporated which have resulted in a better compression ratio and a reduced PRD.
This DDC technique works with only odd samples of ECG signal. It halves the sampling frequency. The waveform is reconstructed using interpolation with 2, which increases the sampling rate of compressed sequence by a factor of 2.
This is an extension of the AZTEC technique. It employs a variable threshold which makes it a self adaptive algorithm [1]. Self-adaptive here implies that the algorithm is intelligent enough to use a higher threshold value for low information region and vice-versa. Higher threshold in low information region i.e. (region with less significant data and more redundant data) ensures a higher compression ratio, thereby eliminating more redundancies. For similar reasons we have low threshold for high information region.
The CORTES method determines on the basis of the length of the line produced post AZTEC as to which of the TP or AZTEC processed results will be saved. This length is compared to a threshold value. If the length is greater than the threshold the AZTEC data is saved else the outcome of TP is recorded. However, this technique gave a CR of approximately 4.8:1 for a PRD of 7 as evaluated by J.P. Abenstein [11]. Hence, a need was felt to further improve the CR of CORTES without tampering much with the PRD.
The proposed hybrid method works similar to the CORTES algorithm. The only difference is that the original algorithm used AZTEC and TP methods. However, in this work we have attempted to amalgamate TP with the dynamic modified AZTEC algorithm.
The steps are as follows:


If sign=1, the slope is assumed to be going up else for sign=0, the slope goes down. For the case when both the directions are the same, it is assumed that the next sample has the final elevation of the slope. Also, one more slope is added to the slope length. This is followed by the resetting of the statistical parameters. Case 3: For ln=1, the entire process for case 2 is repeated except that here it is assumed that the sample after the next has the final elevation of the slope. Also, two more samples are added to the slope length. The slope mode is then terminated. If ln > 3, amplitude (mean) and length of plateaus are computed
The flowchart for the complete process is illustrated in Figure 1.
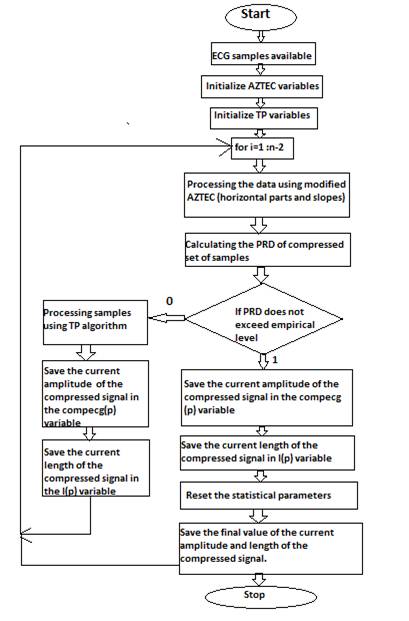
Figure 1. Flowchart for Modified CORTES
The TP part is reconstructed using interpolation by 2. For the modified AZTEC part, reconstruction of slopes and plateaus is carried out separately. For slopes, the intermediate points are calculated and interpolated. The plateaus are reconstructed by repeating the same amplitude for fixed number of times.
Previously, the CORTES method saved either the results of AZTEC or TP data merely on the basis of the length of the plateau produced after AZTEC compression. Slopes had no role to play.
However, in the modified CORTES scheme, both plateaus and slopes have been considered determining factors. The results have verified that this step has only proved beneficial in all respects. Not only did it boost the Compression Ratio but it also immensely reduced the PRD giving us both small compressed file size and accurately reconstructed ECG signal.
The program was tested in the Matlab environment and the results have been summarized in the Table 1. For the section with modified AZTEC the authors used an initial threshold of 0.05 and initialized C1 as 1 and C2 as 0.3 in the expressions for criterion function and threshold respectively, for optimum results. Also, an initial empirical level for PRD is set as 10% so that even in the worst of cases the deviation of the reconstructed signal from the original one doesn't exceed the specified level. The authors have obtained compression ratio as high as 19 without compromising the quality of the reconstructed signal as the corresponding PRD is quite low. Thus, the modified CORTES scheme successfully satisfies the basic requisities of small compressed file size and accurate signal reconstruction.
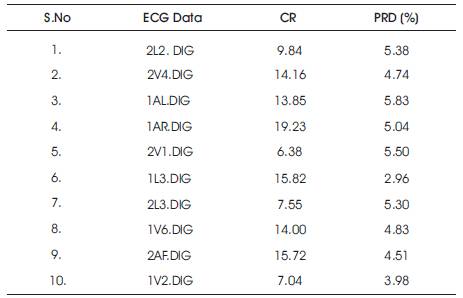
Table 1. Summary of the results obtained for D- 00001.DCD
The corresponding Matlab waveforms are obtained and illustrated: Figure 2 to Figure 11 show two sets of MATLAB waveforms, original and reconstructed. The original waveforms are signals obtained from cse database. The signals are first compressed and then reconstructed using modified CORTES.
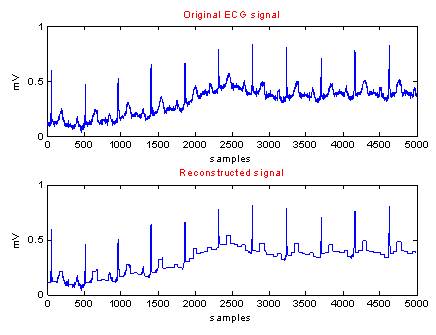
Figure 2. Original and Reconstructed Waveforms using Modified CORTES for Data 2L2.DIG

Figure 3. Original and Reconstructed Waveforms using Modified CORTES for Data 2V4.DIG
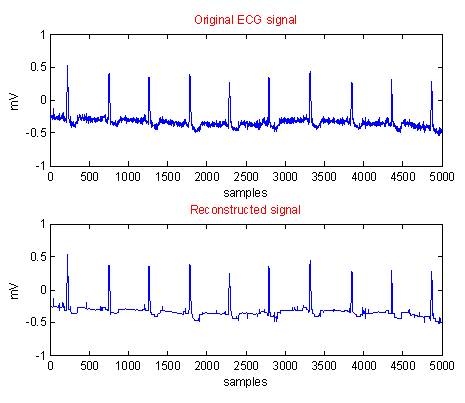
Figure 4. Original and Reconstructed Waveforms using Modified CORTES for Data 1AL.DIG
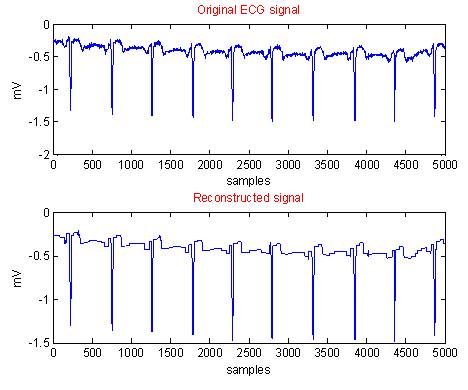
Figure 5. Original and Reconstructed Waveforms using Modified CORTES for Data 1AR.DIG
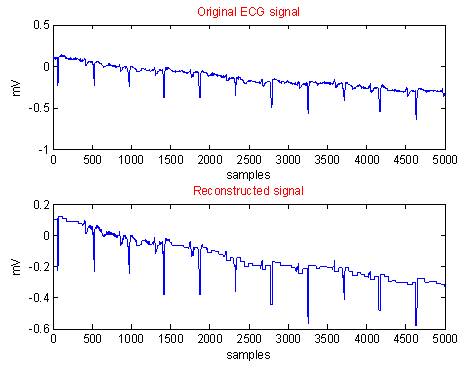
Figure 6. Original and Reconstructed Waveforms using Modified CORTES for Data 2V1.DIG
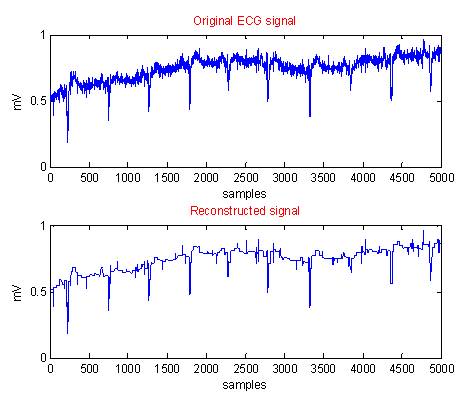
Figure 7. Original and Reconstructed Waveforms using Modified CORTES for Data 1L3.DIG

Figure 8. Original and Reconstructed Waveforms using Modified CORTES for Data 2L3.DIG
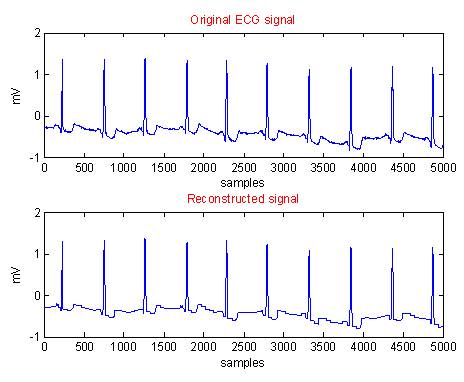
Figure 9. Original and Reconstructed Waveforms using Modified CORTES for Data 1V6.DIG
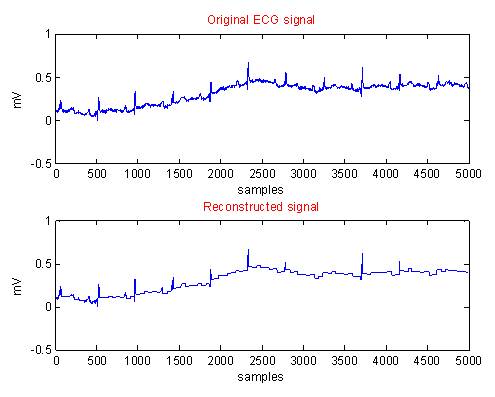
Figure 10. Original and Reconstructed Waveforms using Modified CORTES for Data 2AF.DIG
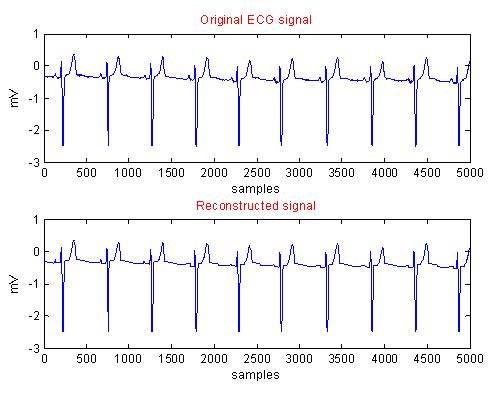
Figure 11. Original and Reconstructed Waveforms using Modified CORTES for Data 1V2.DIG
In each case, i.e from Figure 2 to Figure 11, the first graph depicts the original ECG signal with 5000 samples and an amplitude ranging between -3 to 3 mV. The second graph illustrates the reconstructed ECG using modified CORTES.
The original CORTES scheme though a hybrid provided a limited compression ratio up to 5. However, with minute changes made in the algorithm, the authors obtained better results. Incorporating the dynamic modified AZTEC scheme in place of the simple AZTEC, made the algorithm self adaptive and reliable. The modified CORTES scheme used both slopes and plateaus to determine and save the significant data unlike the original scheme. Also, an initially set value of PRD helped us keep a check on the signal reconstruction. This helped to achieve very high compression ratios for remarkably low PRDs.
The authors are very much thankful to the UGC (MRP) project which is in progress in the Department of Electrical Engineering for providing us some of the ECG data which were used for validating the modified CORTES scheme.