
One of the most significant problems in many application areas is to extract the required signal from background noise. Background noise is random, the occurrence of signal and the behaviour of signal are also random. Therefore, it is practical to deal with the signal extraction problem using methods based on probability theory and statistical estimation. That is to say that signal detection and parameter estimation problems are statistical hypothesis testing problems in Mathematical Statistics. In this paper, signal and noise environment is encountered in active sonar system for target detection. The optimum receiver is presented for range-Doppler- shift processing in a background-noise-limited environment using linear frequency modulation pulse. FFT based implementation for target detection of active sonar system using MATLAB has been shown here.
SONAR (Sound Navigation and Ranging) systems have many similarities to radar and electro- optical systems. The process of sonar is based on the propagation of sound waves between a target and a receiver. The main purpose of sonar is the detection or classification (estimation of position, velocity, and identity) of submerged, floating, or buried objects. The nature of the required object, known as the sonar target, depends on the application. Examples include man-made objects of military interest (a mine or submarine), shipwrecks (as a navigation hazard or archaeological artifact), and fish (the target of interest to a whale or fisherman). In military applications, sonar systems are used for detection, classification, localization, and tracking of submarines, mines, or surface contacts, as well as for communication, navigation, and identification of obstructions or hazards (e.g., polar ice). In commercial applications, sonar is used in fish finders, medical imaging, material inspection, and seismic exploration [2] .
The two most common types of sonar systems are passive and active. Passive sonar includes a receiver but no transmitter. The signal to be detected is then the sound emitted by the target. In an active sonar system, waves propagate from a transmitter to a target and back to a receiver, analogous to pulse-echo radar. In addition to these two types, there is also daylight or ambient sonar, where the environment is the source of the sound, which bounces off or is blocked by the target, and the effects of which are observed by the receiver. This latter type of sonar is analogous to human sight [1].
Active sonars employ two broad classes of pulse types. Continuous Wave (CW) is a pulse of constant frequency and duration of seconds. The bandwidth of the pulse, and of the matched filter for optimum detection of this pulse, is 1 /T Hz. Frequency Modulation (FM) is the frequency of the pulse changes during the T second's duration of the pulse. The bandwidth, B, is not now the inverse of the pulse length [3].
Active sonars know more about the signal to be detected, and therefore the receiver is designed to match the signal, i.e., it uses matched filter processing. But the background, against which the signal has to be detected, contains reverberation in addition to the ambient and self-noise of passive sonars. This additional background is all important in active systems and the designer must be aware of its magnitude and how to discriminate against it.
Sonar waveforms are transmitted into the ocean, and their echo signals are processed for information pertaining to range and velocity characteristics of any scatterers, that the signals encounter [6,7]. In many ocean environments, active sonar systems suffer from reverberation or clutter typified by high false alarm rates (e.g., for low- and midfrequencies see [8-12]). The ability to successfully estimate these scatterer parameters in different situations depends on the sonar waveforms used to gather this information. Some waveforms have good delay (or range) resolution but poor Doppler (or velocity) resolution, while others exhibit excellent Doppler resolution but inferior delay resolution. The detection of a scatterer and the estimation of its parameters are some of the main goals of active sonar. Another main problem is reverberation. It is mainly caused due to multiple reflections of the transmitted signal by the ocean surface, ground, and volume. So, the target detection of active sonar is difficult in the presence of reverberation. Statistical characterizations of reverberation noise are difficult to find out. Here, in this paper, a new methodology for target detection of active sonar is implemented. That is, FFT based implementation for background-noise-limited environment [4-6] using Linear Frequency Modulation (LFM) pulse methodology is shown which gives both Doppler and range resolution and attempts to minimize the effect of reverberation noise on performance.
Section 1 gives brief introduction about mathematical modelling of LFM waveform [4]. Section 2 deals about how LFM is processed in Range-Doppler shift. Finally, FFT based implementation is shown in section 3 followed by the results.
Frequency or phase modulated waveforms can be used to achieve much wider operating bandwidths. Linear Frequency Modulation (LFM) is commonly used [4]. In this case, the frequency is swept linearly across the pulse-width, either upward (up-chirp) or downward (down-chirp). Figure 1 shows a typical example of an LFM waveform. LFM can be mathematically written as

where f0 is the center frequency, and  is the sweep rate.
is the sweep rate.
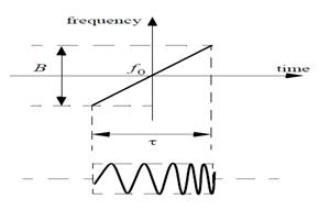
Figure 1. Typical LFM waveform up-chirp
Consider the optimum detectors for the LFM pulse in background noise limited environment. A statistical characterization of reverberation noise is necessary to derive the optimum detector in reverberation noise-limited environment. Because of the problems in obtaining such a characterization in practice, the detector is optimised for the background noise limited case and attempt to minimize the effect of reverberation noise on performance is often used [4, 6]. Parameters under the control of the design engineer are 1. Pulse type, 2. Pulse length, 3. Sweep rate in LFM.
Consider the LFM pulse, assuming that it is operating in zero which means white. The optimum detector is just the quadrature receiver as shown in Figure 2. The number of samples that is summed is set equal to the length of the pulse. The fact that the quadrature receiver is optimum detector is reasonable, because the problem of detecting LFM pulse is equivalent to that of detecting a sinusoidal signal of finite duration in noise.
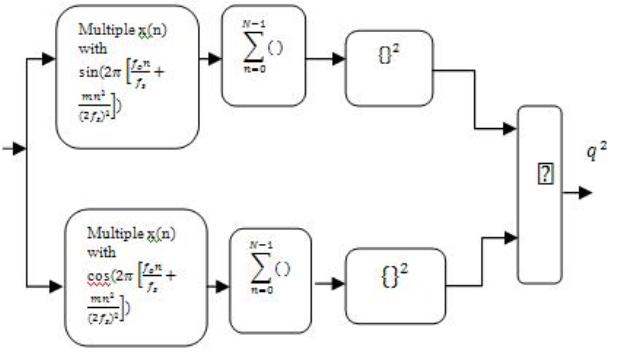
Figure 2. Quadrature receiver (number of samples summed equals to the length of the LFM pulse)
That is, the received signal with a store replica of the LFM pulse is correlated.
Now involving two variables, the hypotheses are

The composite receiver consists of the set of optimum detector, adjusted to the discrete frequencies γi , and j=1……….J and calculated at a set of discrete time, ni, i=1, 2 ...I. At each value of ni, the maximum output of J detectors is compared to the threshold. If the maximum output exceeds the threshold, the frequency value to which the detector is matched serves as the estimation of γ or Doppler shift. The time at which the detection occurs is the estimate of range.
Optimum detector is quadrature receiver shown in Figure 2. A bank of such detectors is implemented in parallel, where each detector is adjusted to a separate frequency, 
 . At the ith time, the output of the jth optimum detector is given by
. At the ith time, the output of the jth optimum detector is given by

The implementation of multiple alternative hypotheses is as shown in Figure 3.
Consider a set of LFM with the centre frequency of 3 Hz and lengths ranging from 5ms to 1s. Consider sweep extent is 200Hz. Such a set of pulse lengths allows us to minimise the effect of reverberation noise pulse for contacts with various values of Doppler shift [3]. Assuming that the maximum velocity is 30knots in magnitude and c=3000knots, the compression parameter at maximum v,  will fall in the range of -0.02≤ δ≤ 0.02.Therefore maximum Doppler shift is equal to 60Hz.
will fall in the range of -0.02≤ δ≤ 0.02.Therefore maximum Doppler shift is equal to 60Hz.
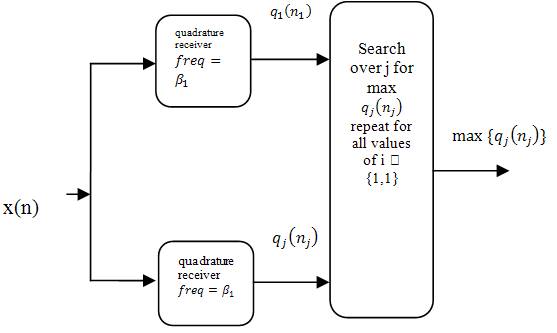
Figure 3. Implementation of the multiple alternative hypotheses test for range and Doppler shift
To obtain an FFT based implementation for 62.5 to 1000ms pulses, an approximate value of the sampling frequency at the input to the FFT is obtained by considering the effects of the spectrum with Doppler shift. The spectrum of the transmitted pulse is equal to

The width of the spectrum between fast zero crossings is f=2/T, where T is the pulse duration in seconds. Because this frequency width varies inversely with T, it achieves a maximum value of 32Hz for the 62.5ms pulse. As a result of Doppler shift, the received centre frequency occurs in the range of fo-60≤ f ≤ fo+60. After shifting the centre of spectrum zero frequency, the highest frequency in this baseband data is then 60+32/2=76Hz. Selecting a sampling frequency of 256Hz at the input to the FFT results in a transition region of the low pass filter of fa -f p=(256-76)- 76=104Hz. Such a transition region is provided by FIR filter of reasonable length.
To establish the sampling frequency for ADC, the highest frequency in the analog data is equal to the sum of the normal centre frequency, the maximum Doppler shift and half of the maximum power spectral width. The 5 ms pulse has a spectral width of 400Hz centred on f0. Therefore, the highest frequency in the analog signal is 3260 Hz. If aliasing is allowed in the transition region of analog filter, a sampling frequency of 8192Hz results in transition region of fp /(f s-f p) which is 0.66. This corresponds to a 6-pole 6-zero elliptic anti aliasing filter. It is desirable to use a short analog filter by oversampling the analog filter 16384Hz.
By considering the sampling frequency as 16384Hz, centre frequency as 3 KHz, velocity of sound as 1500m/s, chirp bandwidth as 1000Hz, chirp pulse width as 62.5 ms, and number of samples as 1025; Assuming that the target is present at 8000m, the following results are obtained using MATLAB. The results are shown and the outputs of each block are shown in Figure 4. Then the output of the Square Law Detectors (SLD) shown in Figure4 is compared with the threshold in order to detect that the target is present or not. Figures 5,6,7,8,9 and 10 show the compared results of Square Law Detectors.

Figure 4. Signal processing for the LFM pulse.
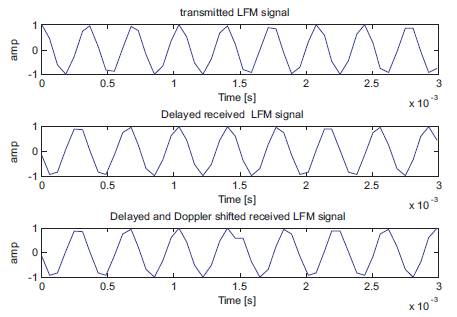
Figure 5. a. Transmitted LFM signal, b. Delayed received LFM signal, c. Delayed and Doppler shifted received LFM signal
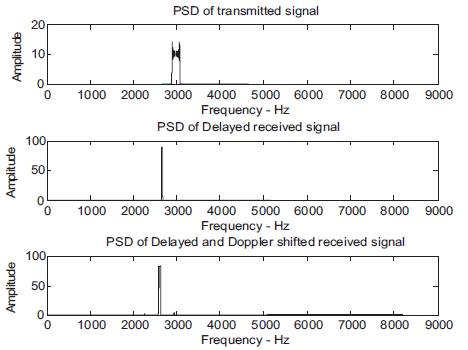
Figure 6. a. PSD of Transmitted LFM signal, b. PSD of Delayed received LFM signal, c. PSD of Delayed and Doppler shifted received LFM signal
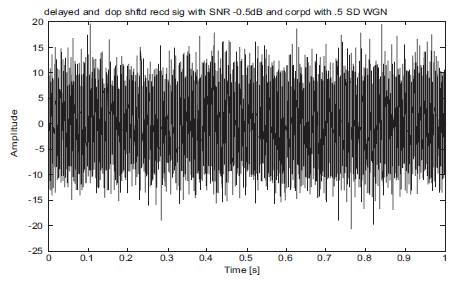
Figure 7. Received Signal with White Gaussian Noise
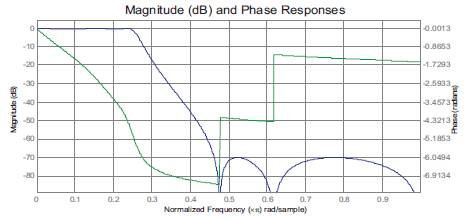
Figure 8. Output of Elliptic Filter Of 6 Poles And 6 Zeros
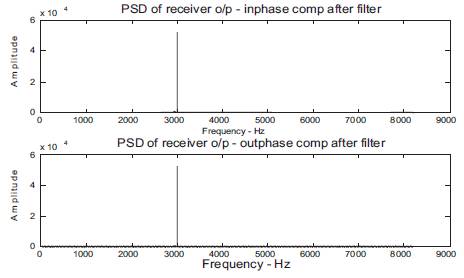
Figure 9. PSD of receiver output inphase and outphase components after filter
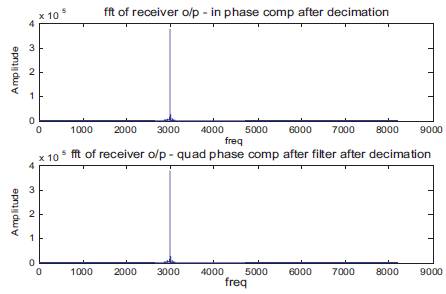
Figure 10. FFT of receiver output inphase and outphase components after filter after decimation
The FFT based implementation of LFM active sonar under noise background environment is implemented using MATLAB successfully and the results are shown. The threshold using Neyman-Pearson (NP) criterion is found out. The maximum output of the detector is compared to that threshold in order to detect the target presence. The target presence is shown in command window. FFT of received Doppler shift signal is shown. The resolution of the FFT is as fine as 3-dB Doppler shift intercept of the ambiguity diagram. At output of the filter the length of the FFT is given by Tfs=265.