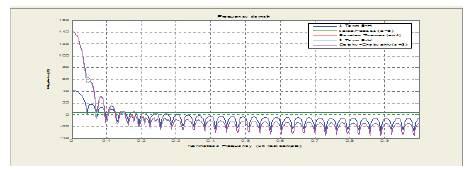
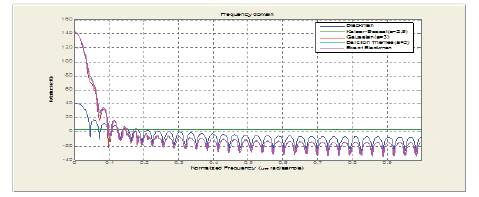
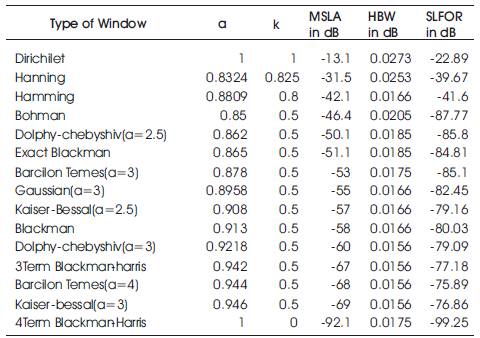
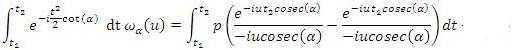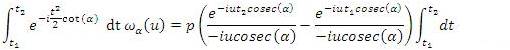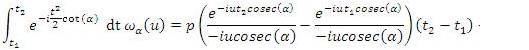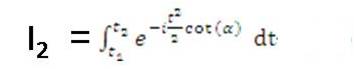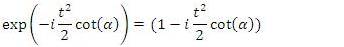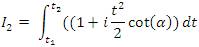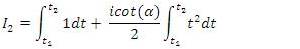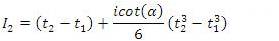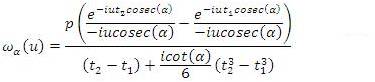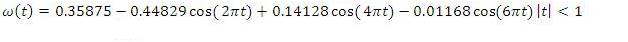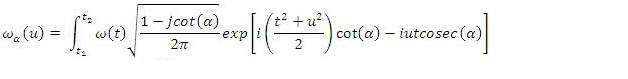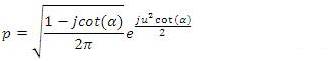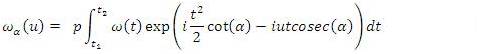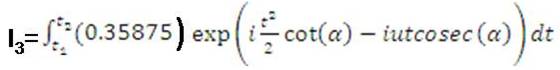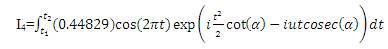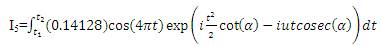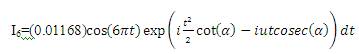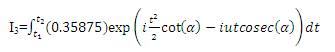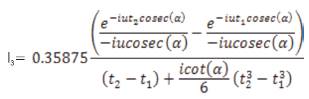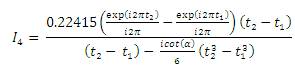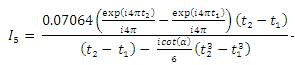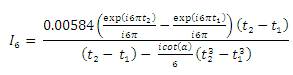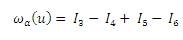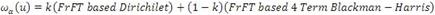Table 1. Spectral Parameters of various windows using Fractional Fourier Transform
An attempt is made such that all existing windows like Bartlett, Hanning, Hamming, Bohman etc. spectral parameters are derived by blending of FRFT of Dirichlet window and FRFT of Blackman-harris window with Al-aloui operator as shown in Table 1 and from the graphs Figure 1 to Figure 3, and to understand the methodology of this paper is modelled as shown in Figure 4. This formula also generalized spectral analysis of forthcoming windows by simply replacing highest possible MSLA with newely possible highest MSLA of forthcoming windows.
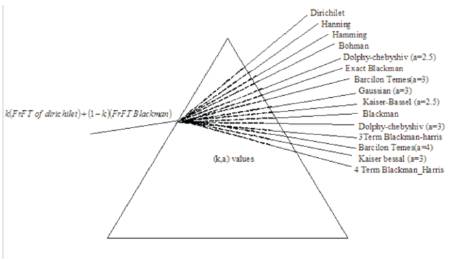
Figure 4. Generalization of all window functions using proposed formula
References
[1]. Fedric J Harris (1978). “On the use of windows for harmonic Analysis with the Discrete Fourier Transform.” Proceedings by IEEE, Vol-66,No:1January.
[2]. P.V.Muralidhar, D.Nataraj, V.Lokeshraju, Dr.S.K.Nayak (2010). “Implementation of different FIR High pass filters using Fractional Kaiserwindow”, Vol:2, DOI:10.1109/ICSPS. 2010.5555740, Publishing year:, pages(V2-651)-(V2-655).
[3]. John G. Proakis, Dimitris G.Manolakis “Digital signal processing, principles, Algorithms and Applications”, Pearson prentice Hall.ISBN:978-81-317-1000-5.
[4]. Miguel Angel Platas-Garzan, JoseAntoniodela o Serena (2011). “Dynamic harmonic Analysis Through Taylor-Fourier Transform”, IEEE Transactions on Instrumentation and Measurement, Vol:60,No:3,march- 2011.
[5]. L.R. Rabiner, B. Gold (1975). “Theory and Applications of Digital Signal Processing”, Prentice-Hall.
[6]. Dr.B.S. Grewal (2006). “Engineering Mathematics”, ISBN NO:81-7409-2196,25th edition, October, Khanna Publications.
[7]. Alok Jain, Rajiv Saxena, S.C. Saxena (2006). “Anti- Image FIR Filters for large Interpolation factors”, Signal Processing, 86 3240-3245. Science Direct-Elsevier publications.
[8]. Sanjay Kumar, KulbirSingh, Rajiv Saxena (2011). “Analysis of Dirichlet and Generalized Hamming window functions in the Fractional Fourier Transform Domains”. Signal Processing, 91 600.606-Science Direct-Elsevier Publications.
[9]. Ashutosh Datar, Alok Jain, Pramod Chandra Sharma (2013). ”Design and performance Analysis of adjustable window functions based cosine modulated filter banks”, Digital Signal Processing, 23 412-417-Elsevier publications.
[10]. Kemal Avsi, Arif Nacaroglu- “Cosh window family and it 's applications to FIR filter design”, Int.J.Electron.Commun.-(AEU) 63(2009)907-916.
[11]. W. Estimator (1989) “IEEE Transactions on Acoustics, Speech, and Signal Processing”, Vol.37,No:2, February 1989.
[12]. Artyum M.Grigoryan (2005). “Fourier Transform representation by Frequency-Time Wavelets”. IEEE Transactions on Signal Processing, Vol-53,No:7, July.
[13]. Namias. (1980). V-“The FRFT and Time Frequency representation”, J.Inst. Math. Applications, Vol. 25, pp.241- 265.
[14]. Soo-Chang pei, Mon Hung Yeh, TzyyliangLuo (1999). “Fractional Fourier Series Expansion for Finite signals and Dual Extension to Discrete-Time Fractional Fourier Transform”. IEEE Transactions on Signal Processing, Vol:47, No:10.
[15]. Soo-Chang pei (2009). “Two-Dimensional Affine generalized Fractional Fourier Transform”. IEEE Transactions on Signal Processing, Vol: 49, No:4, April.
[16]. I. Samil Yetik, M. AlperKutay, Haldun .M. Ozaktas (2001). “Image representation and compression with the Fractional Fourier Transform”, Optics communications, Vol 197, pp.275-278,Elsevier Publications
[17]. V. AshokNarayanan, K.M.M. Prabhu (2003). “The FRFT:Theor y, Implementation and error Analysis”, Microprocessor and Microsystems Vol 27, pp 511-521, Elsevier Publications.
[18]. Ran Tao, Kiang-Yi meng, Yue Wang (2010). “Image encryption with multi orders Fractional Fourier Transforms”, IEEE transactions on Information Forensics and Security, Vol:05, No:04, December
[19]. P.V. Muralidhar, A.S. SrnivasaRao, Dr.S.K. Nayak (2009). “Spectral Interpretation of Sinusoidal wave using Fractional Fourier Transform based FIR window functions”, Vol:04,N0:6,PP:652-657, International Review on computers and software, November.
[20]. Al-Alaoui (2008). Operator and the new transformation polynomials for discretization of analogue systems”. January, Springer-Verlag, Vol. 90, Issue 6, pp 455- 467.
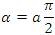 could not hold good for generalization of FRFT to FT [12]. In this proposed Derivatrion of FRFT, an attempt is made to study the variations of window parameters like HBW, MSLA and MSLFOR by different values of fluid parameter of FRFT to FT at
could not hold good for generalization of FRFT to FT [12]. In this proposed Derivatrion of FRFT, an attempt is made to study the variations of window parameters like HBW, MSLA and MSLFOR by different values of fluid parameter of FRFT to FT at 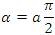 . This paper is organized as follows. Section 1 gives an overview of FRFT, mathematical model of different windows like dirichlet and Blackman window functions. Section 2 presents generalization of different window functions using the proposed formula in equation (34). Conclusion is discussed in the last Section.
. This paper is organized as follows. Section 1 gives an overview of FRFT, mathematical model of different windows like dirichlet and Blackman window functions. Section 2 presents generalization of different window functions using the proposed formula in equation (34). Conclusion is discussed in the last Section.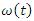 is defined through an interval
is defined through an interval 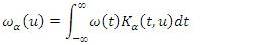
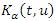 of the FRFT is given by
of the FRFT is given by
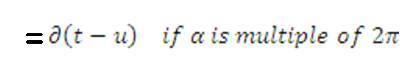

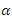 indicates rotation of angle of the Transformed signal for FRFT.
indicates rotation of angle of the Transformed signal for FRFT.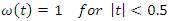
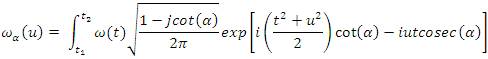
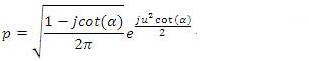
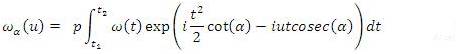
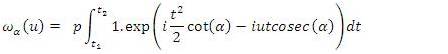
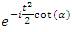 , you will get
, you will get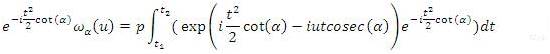
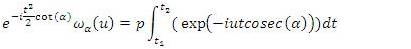
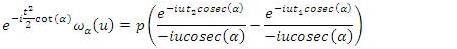
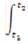 on both sides, results to
on both sides, results to