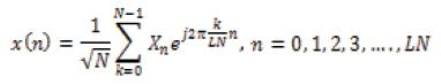
For high data rate communication, Orthogonal Frequency Division Multiplexing technique is most effective & it is widely used for various wireless communications like Digital Video Broadcasting(DVB), Digital Audio Broadcasting (DAB), WiMAX etc. High Peak to Average Power ratio of an OFDM signal is the main drawback of this parallel transmission scheme. Several methods are available to reduce high PAPR of OFDM signal like Clipping, Tone Reservation, Tone Injection, Companding, Partial Transmit Sequence etc. Among these methods PTS is the most powerful method to reduce PAPR of OFDM. In this paper, the authors describe the performance of Partial Transmit Sequence technique applied to the OFDM signal to reduce PAPR, & shows the BER (Bit Error Rate) performance improvement after PAPR reduction.This paper also shows that the computational complexity is a drawback of PTS.
OFDM is a popular modulation technique with many desirable qualities like its excellent robust performance on fading channels & for digital multicarrier modulation [1]. The fading effects are solved by dividing the data into a large number of narrowband parallel channels as used in OFDM [2]. The high peak to average power ratio is a drawback of OFDM signals[3]. The desirable attributes of OFDM come at expenses of large envelope variations. Such signal envelops or amplitude variations can be difficult for the power amplifier to accommodate, resulting in either low poor efficiency or clipping of amplitude. [1].
There has been a significant amount of research devoted to the development of PAPR reduction algorithms for OFDM, which improve the PAPR performance of OFDM signal. Some methods are clipping, tone reservation, tone injection, selective mapping & partial transmit sequence [7,8,12]. PTS is a famous one, which provides better system performance[3]. PTS scheme is the most efficient approach & distortion less scheme for PAPR reduction by optimally combining signal sub-blocks [4].
The PTS approach is based on merging signal sub blocks which are optimally phase shifted by certain phase factors. However, it requires multiple Inverse Fast Fourier Transforms (IFFT) which results in a high computational complexity of practical systems [7,8]. Therefore, the main challenge is to reduce the computational complexity while maintaining the good PAPR reduction [5].
In section 1 the authors present the OFDM system model & PAPR and CCDF (Complimentary Cummulative distribution Function) of OFDM signal. Section 2 includes the methodology to perform PTS technique for PAPR reduction of OFDM signal generated by different modulation schemes & also discusses the complexity and system performance. Section 3 includes the simulation results and conclusion.
The block diagram of an OFDM system model is shown in Figure 1. In OFDM system, a block of N symbols is formed with each symbol modulating by one set of sub-carrier. Then, an OFDM signal is obtained by summing up all the N modulated independent sub-carriers, Where N is the number of sub carriers. The sub carriers are chosen to be orthogonal such that the adjacent sub carrier separation f= 1/T. where T is OFDM symbol duration [6]. The mathematical representation of OFDM signal can be written as [9]
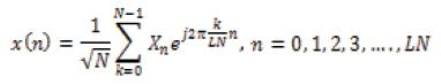
Where N is the number of sub carrier & L is oversampling factor. The sub carrier vector is formed by using certain modulation schemes such as QAM & QPSK etc. [5]. After that the IFFT is performed & guard interval is inserted in the form of cyclic prefix. Then, this signal is transmitted on the adaptive white Gaussian channel. At the receiver side the reverse process is performed & the signal is received in distorted form. The spectrum of original OFDM signal generated by the 16-QAM scheme is shown in Figure 2. Advantages of OFDM signal is that, it can easily adjust to severe channel conditions, is robust against ISI and fading caused by multipath and provide high spectral efficiency. The high power amplifier is very susceptible to the variation in signal amplitudes due to its nonlinear characteristic [10]. Due to the variation of OFDM signal amplitudes; PAPR of Signal is very high. The PAPR for OFDM signal is given by Muller & Hubber & equation as
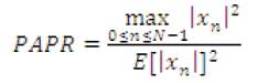
Where E{.}denotes the expected value. When the oversampling factor is 4 then the PAPR for discrete time & continuous time is same [8].
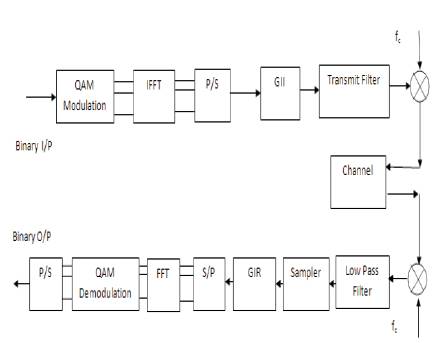
Figure 1. Block Diagram of OFDM System
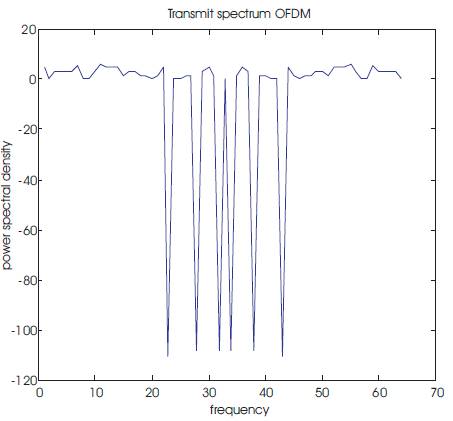
Figure 2. Spectrum of Original OFDM Signal
Due to high PAPR of OFDM, HPA will introduce intermodulation between the different sub-carriers and introduce additional interference into the system. The spectrum of receiving an OFDM signal in the presence of adaptive white Gaussian noise channel is shown in Figure 3. This additional interference destroys the BER performance of the system. To improve BER performance, Power amplifier requires a linear work in its linear active region with a huge dynamic range. However, this linear amplifier has poor efficiency and its so expensive [3].
The CCDF of PAPR is a commonly used performance measures for PAPR reduction which is used to estimate the limits for the minimum number of redundant bits required to identify the PAPR sequences [2].
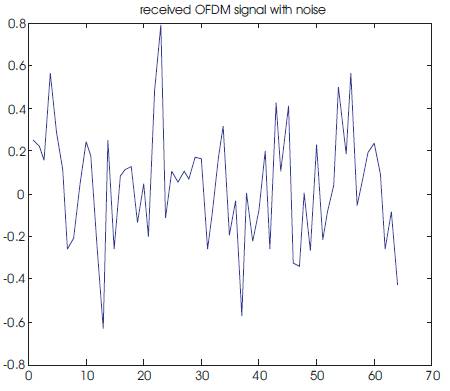
Figure 3. Spectrum of Received OFDM Signal with AWGN Noise
The equation for CCDF can be written as
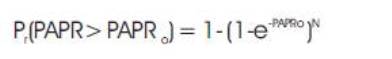
The CCDF of original OFDM signal is shown in Figure 4. The PAPR of original OFDM signal is around 11.8 dB with CCDF of 10-2 , which is very high. To reduce this high PAPR of OFDM signal efficiently, partial transmit sequence technique can be used.
Partial Transmit Sequence technique is a probabilistic (Scrambling) technique [10] which scrambles an input data block of the OFDM symbol & select one of them with the minimum PAPR for transmission as shown in Figure 5 [7].
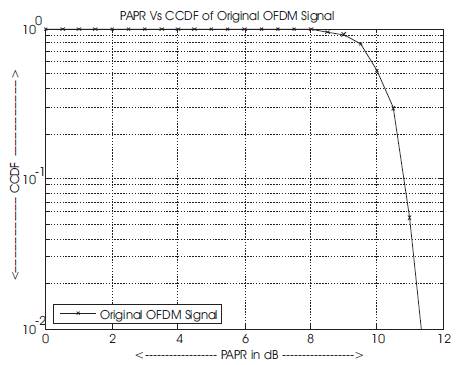
Figure 4. PAPR Vs CCDF of Original OFDM Signal
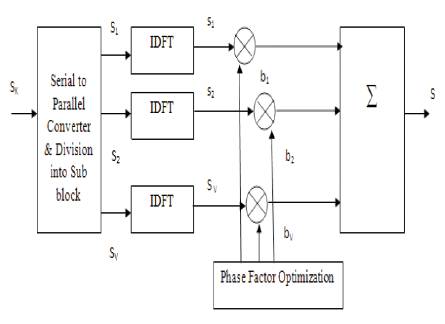
Figure 5. Block Diagram of PTS Technique of PAPR Reduction
In a typical OFDM system with a PTS approach to reduce the PAPR, input data S of N symbols is divided by means of certain partitioning scheme into V disjoint sub blocks. Therefore, we get

Each sub block is of equal size. After that each sub block is phase shifted separately. Let complex phase factor be
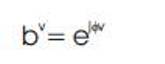
Where v= 1 2 3….V
After taking its IFFT it gives
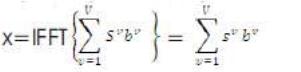
Where sv is referred to as a partial transmit sequence (PTS). The phase factor is selected so that the PAPR can be minimized. So the received signal with lowest PAPR can be given as
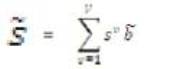
Figure 6 shows the basic methodology to perform the PTS technique for PAPR reduction of OFDM signal. To choose the optimum phase weighting factor for each input sequence we have to verify Wv-1 possible combinations. At the receiver for decoding the data, side information is required in the form of phase factor i.e. log2 Wv-1 . So the authors can say that, in PTS scheme the computational complexity is very large[12].
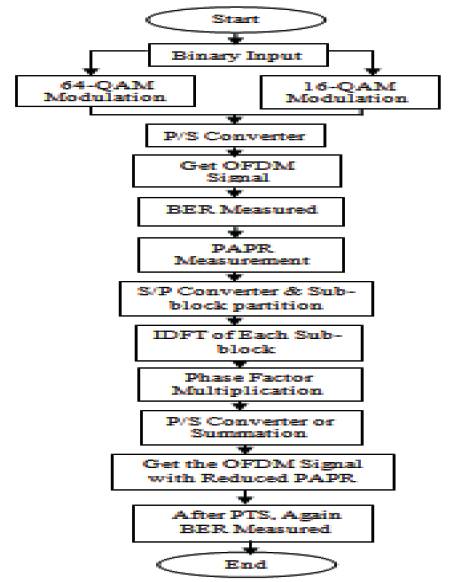
Figure 6. Methodology to Perform PAPR Reduction of OFDM Using PTS Scheme
We have different kinds of optimization used to optimize the phase factor in a PTS scheme like Particle Swarm optimization [4, 18], Cross Entropy[15, 16] Artificial Bee Colony [17, 18], Harmony Search optimization [21-24] etc. These sub optimal schemes offer the best combination of the phase factor with very less computational complexity& at the same time, it gives a superior PAPR performance.
Sub block partition schemes used in PTS are pseudorandom, adjacent & interleaved. These are shown in Figure 7. The performance of pseudo random sub block partition scheme is the best compared to later methods. But the hardware complexity is very large in the pseudo random scheme [8, 9].
In this paper the authors mainly focus on Partial transmit Sequence technique, for PAPR reduction of OFDM signal. The required simulation parameters are included in Table I. Here the OFDM signal is generated by using QAM modulation scheme. The QAM modulation is employed with N= 256 subcarriers. The phase weighting factor W= [1,-1] has been used. The sampling rates for an accurate PAPR need to be increased by 4 times. The number of OFDM blocks for iteration is 10000.The input data are divided into 4 sub blocks using adjacent partition schemes.
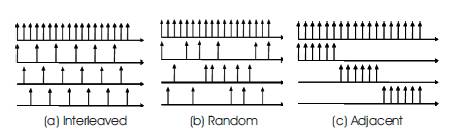
Figure 7 (a) (b) & (c) Sub block Partition Mechanism

Table 1. Simulation Parameters
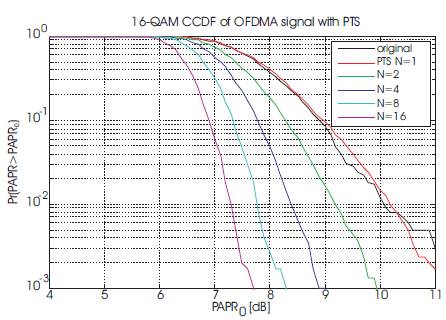
Figure 8. PAPR Performance of a 16 QAM/OFDM System with PTS Technique When the Number of Sub -block Varies
Figure 8 shows the PAPR performance of a 16 QAM/OFDM system with PTS technique when the number of sub block varies. From these simulation results, we can say that for an original OFDM system the PAPR is 11.8 dB, which is greater than the PAPR of OFDM signal after performing PAPR reduction method that is PTS. In PTS technique for M= 2, 4,8,16 sub blocks the PAPR are 9.8dB, 8.9dB & 7.6 dB respectively. When this simulation is performed for different sub blocks, the computational complexity is increases with increase in the number of sub blocks. For 4 sub blocks, & 2 [1 -1] phase factors, the searching complexity is 24 .Similarly for 8 & 16 sub blocks this searching complexity of optimum phase factor is 256 & 65536 respectively, which are very large.
Simulation result shown in Figure 9 gives the comparison of PTS technique performance applied to the OFDM signal generated by 16 & 64 QAM modulation. PAPR of 16QAMOFDM signal, generated by 256 total sub carrier is 11.4dB with CCDF of 10-3 . For sub block M= 4 the PTS assisted 16QAM-OFDM signal, has the PAPR of around 9.2 dB for 10-3 CCDF. With same parameters consideration, the 64QAM –OFDM signal has PAPR of around 11.7dB & after PTS the PAPR is 9.4 dB approximately.
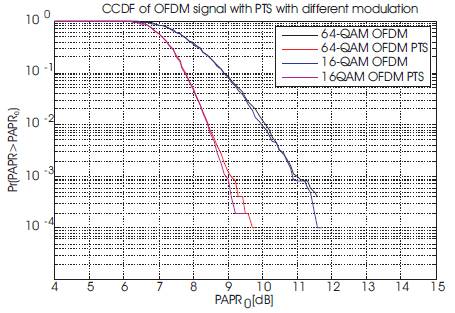
Figure 9. The Comparison of PTS –Technique Applied on OFDM Signal Generated by Different Modulation Schemes
The Bit Error rate versus Signal to Noise ratio of OFDM signal & after PTS technique is shown in Figure 10 & 11. For OFDM - signal the SNR is 18 dB for BER of 10 After applying PTS, Signal to noise ratio is only 16.8 dB. So the authors can say that the BER performance is improved after applying PTS in OFDM.
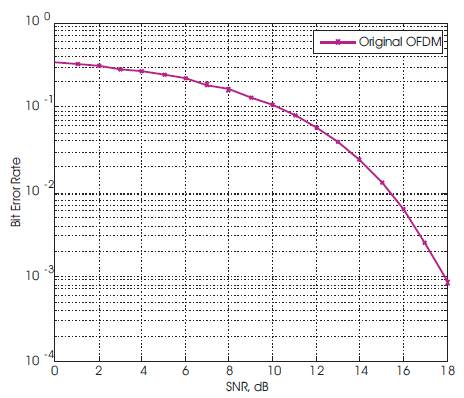
Figure 10. BER Vs SNR of OFDM Signal
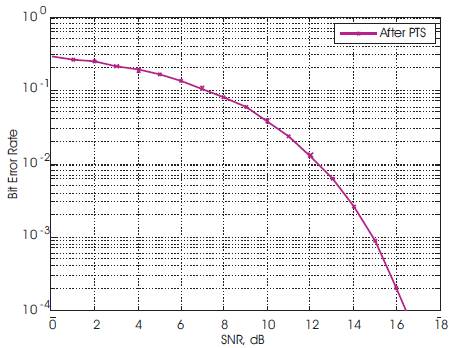
Figure 11. BER Vs SNR of OFDM Signal After PTS

Table 2. Comparison of Performance of PTS Technique for PAPR Reduction of OFDM Signal
Table 2 gives the comparison of performance of PTS technique, used for PAPR reduction of OFDM signal.
The PTS performance evaluation shows that the PAPR is reduced when we increased the number of sub blocks but at the same time searching complexity is increased exponentially with sub blocks. To overcome this problem, the optimization methods like Particle Swarm Optimization (PSO), Artificial Bee Colony (ABC) algorithm, Cross Entropy (CE), Firefly (FF) & Harmony Search algorithms (HS) etc. are used with PTS to optimize the phase factor, which gives a good tradeoff between PAPR per formances & computational complexity. The performance of HS algorithm of optimization depends on the value of pitch adjustment rate & bandwidth [21]. ABC-PTS scheme is slightly degrade the PAPR performance to the conventional PTS but the computational complexity is very less. FF can find the global & local optimum solution of phase factor simultaneously & it reduces the PAPR of OFDM signal effectively [22].
I am very grateful to Chhatarpati Shivaji Institute of Technology, Durg. And I would like to thank my guide Mr. Mangal Singh and Neelam Dewangan for providing me the necessary support & their valuable suggestions to improve my work.