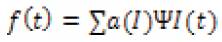
Video Compression is a technique which is used to reduce the amount of data in a video file, inorder to limit the amount of bandwidth or storage space that it requires. Compression technology therefore strives to achieve an optimal trade-off that balances quality with data reduction. Most types of video compression work by comparing a single frame of video to the frames immediately before it and after it, and thus saves only the pieces of the frame that are substantially different. Video compression works best, when only small sections of the video are changing at a time. Video compression is reducing and removing redundant video data so that a video file can be effectively sent over a network and can be stored. With good compression techniques, a reduction in file size can be achieved with little or no adverse effect on the visual quality. However, the video quality can be affected if the file size is further lowered by raising the compression level for a given compression technique.

Compression process involves applying an algorithm to the source video to create a compressed file that is ready for transmission or storage. To play the compressed video file, an inverse algorithm is applied to produce a video that shows the same content as the original source video.

A pair of algorithms that works together is called a Video Codec (encoder and decoder). Video codecs of different standards are normally not compatible with each other; which means, video content that is compressed using one standard cannot be decompressed with a different standard. This is because one algorithm cannot correctly decode the output from another algorithm but it is possible to implement many different algorithms in the same software or hardware.

A wavelet is defined as a “Small Wave” that has its energy concentrated in time to provide a tool for the analysis of Transient, Non-stationary, or Time-varying phenomena and it has the oscillating wave-like properties but also has the ability to allow simultaneous time and frequency analysis.

A signal or a function f(t) can be analyzed, described, or processed if it is expressed as a linear decomposition by

[1]

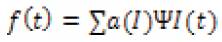
Where, I is an integer index for the sum. Wavelets are functions that satisfy certain mathematical requirements and are used in representing data or other functions. With wavelet analysis, the approximating functions that are contained neatly infinite domains can be used. Wavelets are suited for approximating the data with sharp discontinuities.

The wavelet analysis procedure is to adopt a wavelet prototype function, called a Mother Wavelet or an Analyzing Wavelet. Temporal analysis is performed with a contracted and high-frequency version of the prototype wavelet, Frequency analysis is performed with a dilated and low-frequency version of the same wavelet. The original signal or function can be represented in terms of a wavelet expansion and data operations can be performed using just the corresponding wavelet coefficients. If the best wavelets adapted to the data is chosen, or truncate the coefficients below a threshold, the data is represented sparsely and this sparse coding makes wavelets an excellent tool in the field of data compression.

The Discrete Wavelet Transform (DWT) involves choosing scales and positions based on powers of two and are called dyadic scales and positions. The mother wavelet is rescaled or “dilated” by powers of two and translated by integers.

Specifically, a function f(t) ε L² (R) can be represented as

[2]

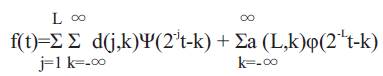
where, Ψ(t) is known as the mother wavelet, φ(t) is known as the scaling function. The numbers a(L, k) are known as the approximation coefficients at scale L and d(j,k) are known as the detail coefficients at scale j.

The approximation and detail coefficients can be expressed as,

[3]

[4]

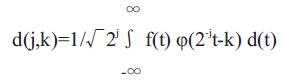
The above two equations give a mathematical relationship to compute the approximation and detail coefficients.

Two dimensional DWT is obtained through the implementation of low pass and high pass filters on rows and columns of image respectively. Low pass and high pass filters are chosen; such that they exactly halve the frequency range between them. This filter pair is called the analysis filter pair. Initially, the low pass filter is applied for each row of data, hence getting the low frequency components of the row and the output data contains frequencies only in the first half of the original frequency range because the low pass filter is a half band filter. Subsequently the high pass filter is applied for the same row of data, and the high pass components are separated, and those high pass components are placed by the side of the low pass components. This procedure is done for all rows. As stated above, the LL band at the highest level can be classified as most important, and the other 'detail' bands can be classified as of less important [1].

DWT is a multispectral technique that is used for converting the signal or image into four different bands i) low-low (LL), ii) low-high (LH), iii) high-low (HL), iv) high-high (HH) as shown in Figure 1.

Wavelet analysis process involves filtering and down sampling and the wavelet reconstruction process involves up sampling and filtering. The process of lengthening a signal component by inserting zeros between samples is known as Upsampling.

The low-frequency content is the most important part for many signals. It is what gives the signal its identity. On the other hand, the high-frequency content, imparts flavor or nuance. The approximations are the high-scale and low-frequency components of the signal. The details are the low-scale and high-frequency components. The basic filtering process is shown in Figure 2.

The original signal, S, passes through two complementary filters and emerges as two signals and they are represented as cA and cD. The process on the right, which includes down sampling, produces DWT coefficients. The detail coefficients cD is small and consists mainly of a high-frequency noise and the approximation coefficients cA contains much less noise than does the original signal. The actual lengths of the approximation and detail coefficient vectors are slightly more than half the length of the original signal and this has to do with the filtering process and the process can be repeated to get multiple-level decomposition.

In filtering part, the choice of filters is crucial in achieving perfect reconstruction of the original signal. Down sampling process of the signal components performed during the decomposition, introduce a distortion called aliasing [2]. By carefully choosing the filters for the decomposition and reconstruction that are closely related (but not identical), effect can be "cancel out".

The low-and high pass decomposition filters (L and H), together with their associated reconstruction filters (L' and H'), form a system called quadrature mirror filters as shown in Figure 3.

Given signal's' is length of N, the DWT consists of log2N stages at most. From the signal's', the first step produces two sets of coefficients: approximation coefficients cA1, and detail coefficients cD1.

These vectors are obtained by convolving 's' with the low-pass filter Lo_D for approximation, and with the high-pass filter Hi_D for detail, followed by dyadic decimation. The next step, splits the approximation coefficients cA1 in two parts by replacing's' by cA1 and its producing cA2 and cD2, and so on.

The discrete wavelet transform can be used to analyze, or decompose signals. This process is called analysis or decomposition. The next half is how those components can be assembled back into the original signal without any loss. This process is known as synthesis or reconstruction and the mathematical manipulation that affects synthesis is called the Inverse Discrete Wavelet Transform (IDWT).

Haar is a wavelet function which applies the easiest, using the least time and it has orthogonal property [3]. The mother wavelet of Haar ψ (x) can be described as the equation

[5]

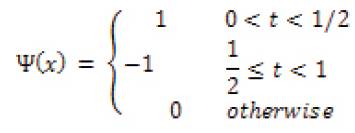
The attracting features of the Haar transform are fast for implementation and are able to analyse the local feature and has applications such as signal and image compression. The Haar wavelet transform has the advantages of being conceptually simple, fast and memory efficient because it can be calculated in place without a temporary array.

The Daubechies wavelets are a family of orthogonal wavelets defining a discrete wavelet transform and characterized by a maximal number of vanishing moments. For each wavelet type of this class, an orthogonal multi resolution analysis is generated by a scaling function [4]. In general the Daubechies wavelets are chosen to have the highest number A of vanishing moments, for given support width N=2A, and among the 2A−1 possible solutions the one is chosen whose scaling filter has external phase.

The names of the Daubechies family wavelets are written dbN, where N is the order of the wavelet. This wavelet type has balanced frequency responses but non-linear phase responses. These wavelets use overlapping windows such that the high frequency coefficient spectrum reflects all high frequency changes. Hence Daubechies wavelets are useful in compression and noise removal of audio signal processing.

Bior or semi-orthogonal wavelet is only orthogonal to the shifted base function under different scale factor, but has no orthogonality in the same scale factor. The mother wavelet of Bior can be described as equation

[6]

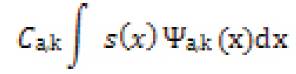
Biorthogonal family of wavelets has the property of linear phase, which is needed for signal and image reconstruction.

Symlet wavelet defines a family of orthogonal wavelets. Symlet wavelet[n] is defined for any positive integer n. The scaling function (Ф) and wavelet function (ψ) have compact support length of 2n. The scaling function has n vanishing moments. Symlet wavelet can be used with such functions as Discrete Wavelet Transform and Wavelet Phi, etc.

It is the ratio of the original signal to the compressed signal [5].

[7]

This indicates the amount of energy retained in the compressed signal as a percentage of the energy of original signal.

[8]

[9]

where, N represents the length of the reconstructed signal, X is the maximum absolute square value of the signal and ׀׀x-r׀׀2 is the energy of the difference between the original and reconstructed signals.

MPEG (Moving Picture Experts Group) is the name of the family of standards used for coding audio and video data in a digital compressed format including data transmission across digital networks. MPEG Video files have the .mpg or .dat extension. MPEG is cross-platform compatible and can be played on all popular computer systems. MPEG uses a type of lossy compression because some data is removed. But the removed data is generally imperceptible to the human eye.

AVI (Audio Video Interleave) is a file format designed to store both audio and video data in a standard package to allow its simultaneous playback. AVI is one of the most commonly used video formats. AVI-formatted files employ the file extension .avi, and are comprised of a header tag followed by a series of chunks of information. The header portion provides details about width, height, and frame rate of the file, while the chunks of information store the actual audio and video data. Advantage of AVI format is its ability to be played on the majority of computers worldwide.

WMV (Windows Media Video) is a video format which is designed to handle all types of video content. These video files can be highly compressed and can be delivered as a continuous flow of data. These video files can be of any size and can be compressed to match many different bandwidths. Using WMV is an excellent way to get file sizes down to reasonable levels while retaining watchable quality. It allows compression of large files without quality losses.

In this paper, input is considered as a 30 seconds video in the formats MPEG, AVI and WMV. The file size of MPEG format is 39.1MB for the given input video. Using online video convertor, MPEG format is converted into the formats AVI and WMV whose file sizes are 34.1MB and 42MB respectively. To analyze the video compression for different wavelets the above 3 formats are compared using the parameters PSNR, Retained Energy and Compression Ratio.

This part has illustrated the final results by comparing the various parameters such as PSNR, Retained Energy, Compression Ratio for HAAR, Db10, Db2, BIOR2.2, sym8 wavelets in each video formats and the results are shown in the following Tables1, 2 and 3.

From the Table 1, we can infer that the Compression Ratio is higher for HAAR wavelet, whereas Retained Energy and PSNR are high for SYM8 wavelet.

From Table 2, we can state that the Compression Ratio is higher for HAAR wavelet, whereas Retained Energy is high for SYM8 wavelet and PSNR is high for BIO2.2.

From Table 3, we observe that the Compression Ratio is high in HAAR wavelet, Retained Energy and PSNR is high in SYM8 wavelet.

Comparison of various parameters PSNR, Retained Energy and Compression Ratio for different wavelets of the video formats MPEG, AVI and WMV is shown in the below Figure 4, 5 and 6 and Tables 4,5,6.

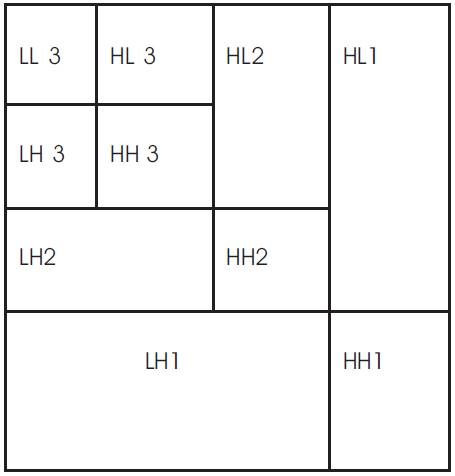
Figure 1. Decomposition of image applying DWT

Figure 2. One stage filtering scheme

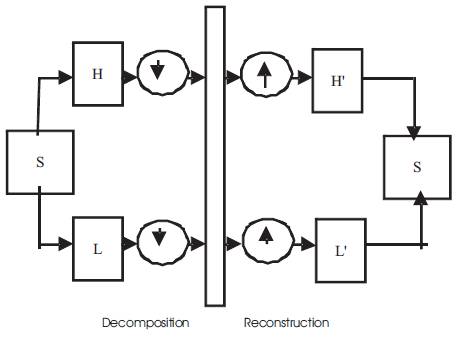
Figure 3. Wavelet Decomposition and Reconstruction

Table 1. Comparison Of Different Wavelets For Compression In Mpeg Video

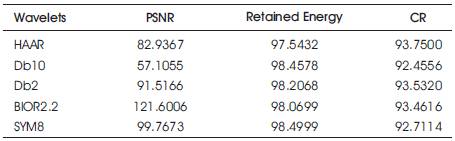
Table 2. Comparison Of Different Wavelets For Compression In Avi Video

Table 3. Comparison Of Different Wavelets For Compression In Wmv Video

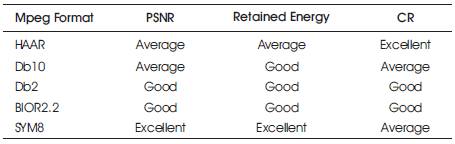
Table 4. Performance Analysis For Mpeg Video Format

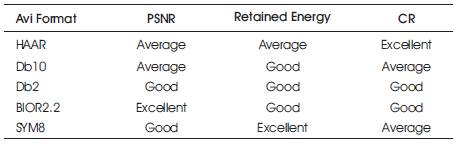
Table 5. Performance Analysis For Avi Video Format

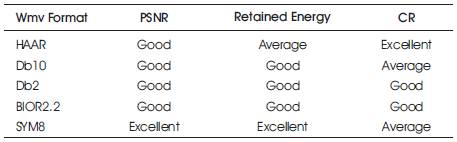
Table 6. Performance Analysis For Wmv Video Format

Figure 4. Comparison of PSNR for different wavelets

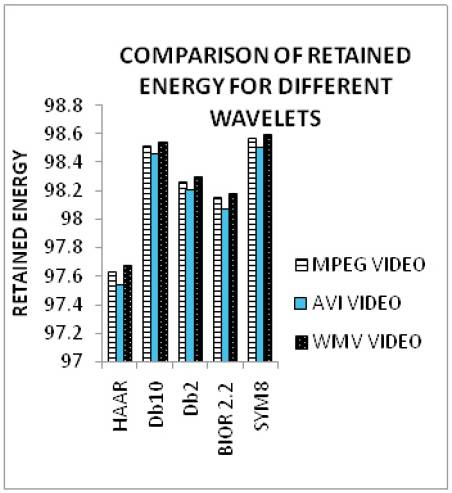
Figure 5. Comparison of Retained Energy for different wavelets

Figure 6. Comparison of Compression Ratio for different wavelets

In this paper, as far as Compression Ratio is concerned, HAAR wavelet is effective and efficient irrespective of the video formats, whereas for Retained Energy, SYM8 wavelet is the best for all video formats and PSNR is best for SYM8 wavelet in MPEG and WMV video formats. We can conclude that HAAR and SYM8 are the efficient wavelets since it has higher Compression Ratio and Retained Energy in all the video formats.