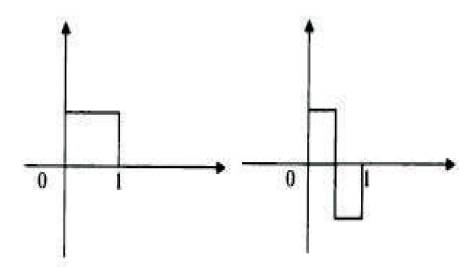
Figure 1. Scaling and Wavelet functions of HAAR
Wavelet Transforms are set of mathematical functions that represent image as a sum of wavelet functions with different locations and scales. Wavelet Transformations provide information in both frequency domain and spatial domain as well, standard de-facto images of varying sizes are subjected to two level decomposition using Wavelet Filter Functions like Haar, Daubechies, Biorthogonal, Coiflets and Symlets etc. The transformed approximation and detail coefficients, typically infinite precision real numbers are quantized such that the more important coefficients are represented with higher accuracy while those with less accuracy are neglected. In quantization input values are mapped to output values, based on particular threshold levels. The quantized coefficients are further coded in a bit stream using Recursive Splitting Huffman Encoding. This study evaluates and compares the merits of selected Wavelet Transform techniques for different filter functions graphically to discuss important features of wavelets in image Compression. Objective fidelity metrics Peak Signal to Noise Ratio (PSNR), Mean Square Error (MSE) and Compression Ratio (CR) obtained are shown graphically.
Taking into consideration the ever-increasing requirements of energy for Biomedical Applications, Computer Graphics and many other web based applications, storage space and channel bandwidth turned out to be the primary constraints in areas of signal and image transmission applications. This created an urge among the world of researchers in the fields of Signal and Image processing to innovate new techniques of compression and decompression of signals, still images and videos of various types and sizes as well [17].
Digital images are normally compressed by eliminating few forms of redundancies contained in the information, specified as under:
Different lossy and lossless compression techniques are under development to ensure fast and reliable operations of compressions of different quality levels, SNR's and MSE's.
[1] Wavelets provide good compression ratios for high resolution images and always perform better i.e Wavelet based JPEG2000 image coders easily outperform the traditional DCT based JPEG image compression techniques in terms of signal to noise ratio and visual quality. Unlike the JPEG technique, wavelets do not exhibit the problem of blocking artifacts but instead allows for degradation of the whole image quality while preserving the significant details of the parent image. In case of wavelet based JPEG2000 image compression system, the entire input image is transformed as a whole and compressed as a single data object rather than block by block basis as in a DCT based compression system. Here the compression is distributed uniformly throughout the entire image to provide better quality of the image [4].
[3] The performance of a wavelet based image coder depends to a large extent on the selected wavelet family. Active research is carried out on multimedia data compression techniques like JPEG, JPEG2000 and MPEG, to achieve high compression ratios and better PSNR, MSE measures without degrading the reconstructed image quality.
This paper is organized as follows. Section 1, briefs about wavelets and proposed encoding methodology. Section 2, elaborates different families of wavelets for image compression. Section 3, presents the Ex perimental analysis of results followed by conclusion section.
Wavelets are mathematical functions that separate data into different frequency components on decomposition and further study, each band of components with resolutions matched to scale. Wavelet transforms have the advantage of analyzing the physical reasons in case of signals having discontinuities and sharp spikes. [15] Wavelet transforms are continuous and discrete type. In case of long signals continuous wavelet transform needs to be integrated all times, Discrete Wavelet Transform (DWT) analyses coefficients based on dyadic scales or scales of powers of two.DWT localizes signals in time and scale, however the DFT or DCT localizes signals in frequency domain.
[5] [16] Wavelet decomposition of input image uses a pair of waveforms to represent the high frequencies corresponding to the detailed parts of an image (wavelet function) clearly showing the Vertical, Horizontal and Diagonal details, while the low frequencies or smooth parts of image (scaling function) correspond to approximation coefficients. [1] If the numbers of high frequency coefficients are very smaller than the threshold they are made Zero without any significant change in the image. If the numbers of zeros are more, greater compression can be achieved. However, as more zeros are obtained more energy is lost [10].The approximation and detail coefficients after two level decomposition are quantized such that the more important coefficients are represented with high accuracy and retained while the less accurate ones are neglected. Quantized coefficients are coded in a bit stream using Recursive Splitting Huffman Encoding to obtain the compressed data. Decompression involves the operations of Huffman decoding and inverse quantization of the compressed output coefficients followed by obtaining the inverse wavelet filter coefficients of selected wavelet transform of choice.
[2] [14] Filter functions of selected families of wavelets Haar, Daubechies, Symlets, Coiflets and biorthogonal wavelets are presented here.
[5] [12] The Haar matrix proposed in 1909 by Alfred Haar is the simplest possible wavelet. It is discontinuous, not differentiable and resembles a step function. Haar wavelet is the simple form of compression involving average and difference terms, by storing the detail coefficients and are used to reconstruct matrix such that the resulting matrix is similar to the initial matrix. It represents same wavelet as Daubechies 1.
WH (X) = {1 0 < x < ½
-1 ½ < x < 1
0 otherwise }
The properties of Haar transform are as listed under:
The compact support of Haar wavelets enable the Haar decomposition to have good time localization i.e Haar coefficients are effective for locating jump discontinuities and efficient representation of signals with small support. The wavelet filter function for Haar wavelet is as shown in Figure 1.

Figure 1. Scaling and Wavelet functions of HAAR
[11] Ingrid Daubechies invented the so called compactly supported, orthonormal wavelets. Daubechies wavelets are written as dbN, where Nis the order, db is the family name of the selected wavelet.
Daubechies wavelets have the highest number of vanishing moments for given support width N=2A, and 2A-1 possible solutions, the one whose scaling filter has external phase is chosen. Daubechies wavelets are used in solving fractal problems and signal discontinuities etc. The wavelet functions are listed below, x-axis represents the time and y-axis represents the frequency [11]. The wavelet filter functions for Daubechies wavelet are as shown in Figure 2.
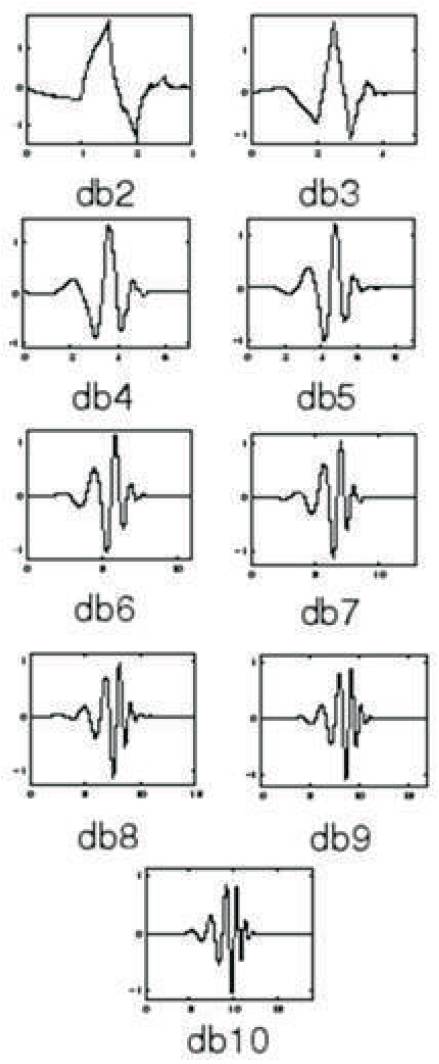
Figure 2. Wavelet Functions of Daubechies
[7] Symlets are a family of symmetric wavelets proposed by Daubechies as a modification of Daubechies wavelets by modifying the construction of dbN. The properties of both wavelet families are similar. Symlets are orthogonal and compactly supported wavelets, they are so designed that they have the least asymmetry and maximum number of vanishing moments for a given compact support. Symlets are found to be more efficient in de-noising applications; Symlets used in practice are also selected even number wavelets as Daubechies. Though Symlets are considered to be symmetrical wavelets they are not perfectly symmetrical. The wavelet filter functions for Symlet wavelet are as shown in Figure 3.
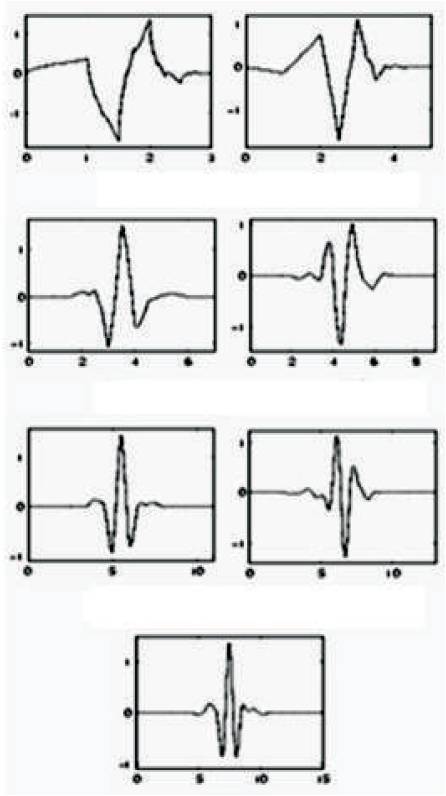
Figure 3. Wavelet functions of Symlets
[8] Biorthogonal wavelets extend the family of orthogonal wavelets; their important applications are especially in the areas of Signal and Image Processing. In particular bi-orthogonal wavelets with compact supports, leading to filter banks are used frequently. The periodic bi-orthogonal wavelet transforms are realized by matrix-vector products with sparse, structured matrices. Since symmetry and Perfect reconstruction are totally incompatible when same FIR filters are used for decomposition as well as reconstruction two wavelets are used instead of one Bi-orthogonal, wavelets, exhibiting the property of linear phase essential for signal and image reconstruction using two wavelets [9], The wavelet filter functions of bi-orthogonal family wavelets are as shown in Figures 4 and 5.
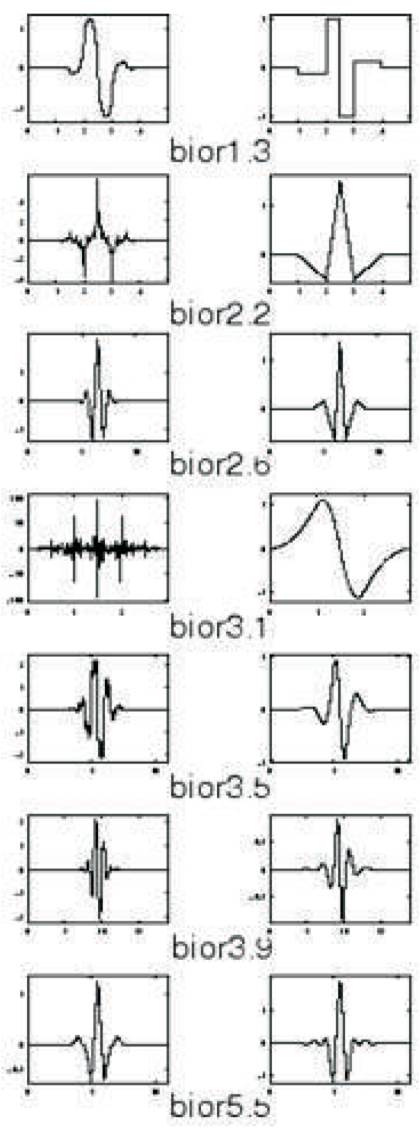
Figure 4. Biorthogonal Wavelet Families
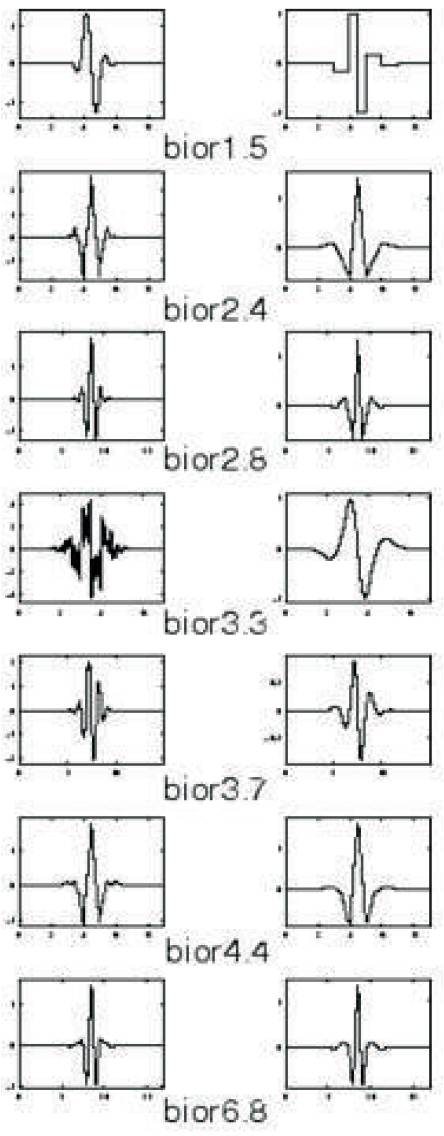
Figure 5. Biorthogonal Wavelet Families
Coiflets are discrete wavelets designed by Ingrid Daubechies, on request by Ronald Coifman, to have scaling functions with vanishing moments. [6] Coiflets and Daubechies wavelets are similar in a certain level, Coiflets are near symmetric and have N/3 vanishing moments and N/3 -1 scaling functions.
One disadvantage with coiflets are they neither have any formula nor any proof of existence [16]. The wavelet filter functions of Coiflet family wavelets are as shown in Figure 6.
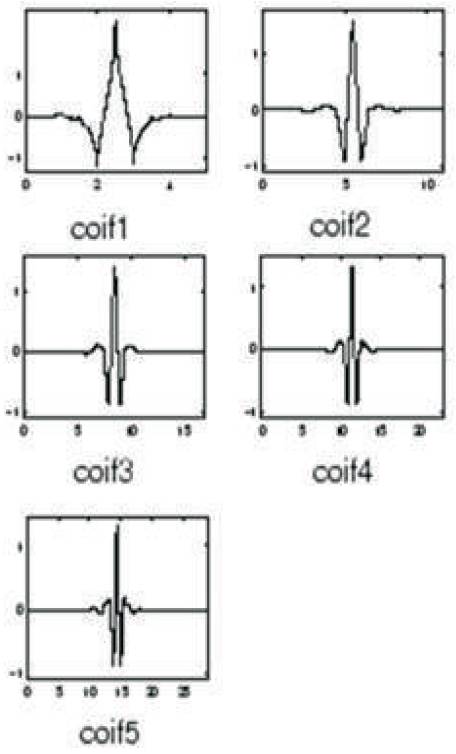
Figure 6. Wavelet functions of Coiflets
Metric values like PSNR, MSE and CR corresponding to the application of Haar, Daubechies, Coiflet and Symlet families of filter functions on standard bench mark gray scale and color images Circuit, Westconcordorthophoto, Lena and color image are shown graphically for the sake of analysis, after matlab simulations.
Figures 7 to 11 imply that, Db2 family produced better PSNR value while the CR is more for Db4 family. Coiflet2 family result in better values of PSNR and CR.SYM8 and SYM2 families produced better PSNR and least CR value. In case of Biorthogonal family wavelets, Bior2.8 has more PSNR value and less CR; in contrast Bior3.3 produced better value of CR.

Figure 7. Daubechies Images

Figure 8. Coiflet Images

Figure 9. Symlet Images

Figure 10. Biorthogonal Images
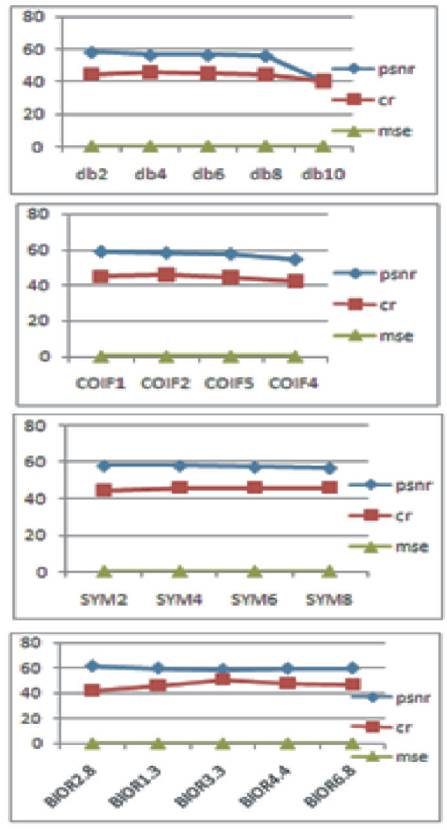
Figure 11. Comparison of PSNR, MSE & CR of different Wavelets on Circuit Image
Figures 12 to 16 of Westconcordorthophoto image imply that, Db4 and Db2 family of wavelets produced large values of PSNR and CR. COIF1 family result in large values of PSNR and CR. Sym2 and SYM4 wavelet families produced better values of PSNR and CR. While Bior4.4 produced better values of PSNR and CR among all biorthogonal family wavelets; in contrast Bior6.8 produced the least value of CR.

Figure 12. Daubechies Images
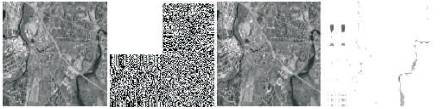
Figure 13. Coiflet Images

Figure 14. Symlet Images

Figure 15. Biorthogonal Images
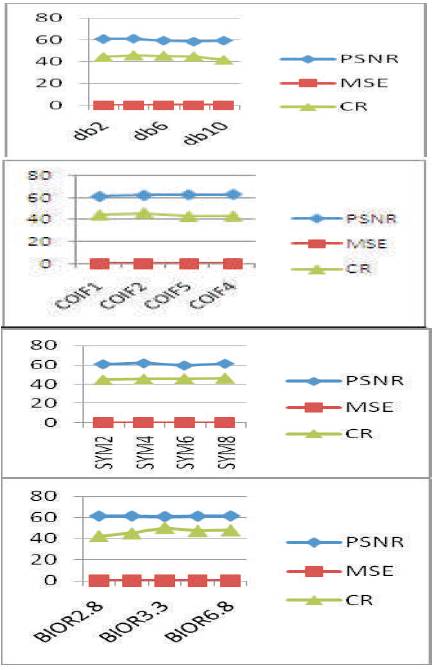
Figure 16. Comparison of PSNR, MSE & CR of different wavelets on Westconcordorthophoto image
Figures 17 to 21 of Lena image imply that, Db10 and Db8 family wavelets produced large values of PSNR and CR of order 60.401 and 57.5724, COIF2 family produced large values of PSNR and CR of 60.4978 and 54.8822.Sym2 and SYM8 family produced better values of PSNR and CR of order 60.4017 and 55.7999. Bior1.3 family produced large PSNR value of 62.6783 while Bior3.3 produced large CR of 58.3209 in contrast Bior4.4 produced the least CR of 51.3042.

Figure 17. Daubechies Images

Figure 18. Coiflet Images

Figure 19. Symlet Images

Figure 20. Biorthogonal Images
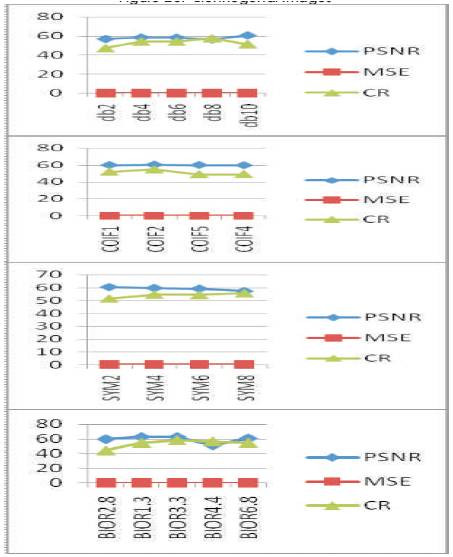
Figure 21. Comparison of PSNR, MSE & CR of different Wavelets on Lena Image
Figures 22 and 23 of color image1 clearly imply that, Db8 and Db4 family of wavelets produced large values of PSNR and CR of order 23.3969 and 44.5106. While Bior1.3 and Bior3.3 family of wavelets produced large values of PSNR and CR of order 22.3844 and 51.2067.
Each of the Figures.7 to 10, 12 to 15 and 17 to 20 contain four images in the order specified as under: Input image, Image showing all coefficients after 2 level decomposition, Output image and Approximation coefficients after 2nd level decomposition.

Figure 22. Daubechies Images

Figure 23. Biorthogonal Images
Though Graphical analysis is performed on many gray scale and color images for encoding and decoding operations of various bench mark images, only few like Circuit, WestConcordorthophoto, Lena and Color etc are discussed in this work. 19 different wavelet filter functions are considered for analysis, totaling to 114 encoding and decoding operations.
The results clearly imply that Biorthogonal functions offer good compression performance while Daubechies performed well statistically. Therefore compression performance is mainly dependent on the image content and size hence it is appropriate to tailor the choice of wavelet based on image size and content for desired quality of reconstructed image.