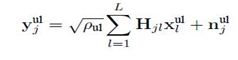
This paper performs analysis of massive Multiple Input Multiple Output (MIMO) system having large number of base station antennas N and user terminals K with uplink and downlink of Time Divison Duplexing system. In this system model, path loss, pilot contamination, and antenna correlation for each link are considered. In this work, estimation of achievable rates with several linear detectors like MF (Matched Filter) and MMSE (Minimum Mean Square Error) are done. Achievable rate versus number of base station antennas N for MF and MMSE are simulated. It is observed that performance of MMSE detector is superior in terms of achievable rate compared to MF detector in massive MIMO system. Secondly, spectral efficiency and energy efficiency of massive MIMO system with imperfect CSI (Channel State Information measured from uplink pilots) is analyzed. In this analysis, MRC (Maximum Ratio Combining) detector and derived spectral efficiency and energy efficiency for different values of transmitted power is used. From simulation, it can be observed that as we increase transmitted power, spectral efficiency is increased but at the cost of energy efficiency. So there is always trade-off between spectral efficiency and energy efficiency. Also it is observed from simulation that as number of base stations is increased, antenna trade-off curve shifts upwards.
In massive MIMO system, a Base Station (BS) equipped with multiple antennas serves a number of users. Such systems have attracted much attention for some time now. Massive MIMO, widely considered a promising candidate for the 5G physical layer, serves every active user all the time / frequency resources with aggressive multiplexing based on measured propagation channels. The most elementary multiplexing signal processing can yield higher spectral efficiency over LTE. Power control ensures that users at the edges of the cell experience the same high throughput that users near the base station enjoy. The radiated power is reduced in proportion to the number of antennas, which in turn, can translate into hundred-fold gains in total energy efficiency. Conservation of energy is very essential in By current scenario of the world and as per survey done in 2013, 69 Giga Watts power is consumed in world-wide telecommunication networks, i.e. equivalent to power consumed by 12 New York cities in a year. So massive MIMO is technological that achieves huge energy efficiency. High energy efficiency is achieved due to concentration of radiated energy on UE. There are several other benefits of Massive MIMO (Marzetta, 2015). There is a uniformly excellent service throughout the cell - regardless of location relative to base station. Robustness to individual element failure occur due to large number of antenna array elements. Massive MIMO can be developed using low power and in-expensive components. It enables large reduction in latency on air interface. Simple and scalable design-employs measured channel characteristics rather than assumed channel characteristics (Marzetta, 2015; Goldsmith, 2005). Resource allocation and processing are simplified, not complicated. Naturally green technology gives superior energy efficiency. In massive MIMO system, antenna configuration may be classified as co-located antenna system and distributed antenna system (Liu et al., 2014). In Co-located antenna system, all the transmitter or receiver antenna are located centrally at one place, whereas in Distributed antenna system, all antennas are uniformly placed along the place (Liu et al., 2014).
Recently, there has been a great deal of interest in Massive MIMO with very large antenna arrays. The design and analysis of very large MU-MIMO or massive MIMO system is quite a new subject that is attracting extensive interest (Sun et al., 2017). With a very large antenna array, things that were random before, start to appear deterministic. As a result, the effect of small-scale fading can be equalized (Goldsmith, 2005). Moreover, when the number of BS antennas (N) grow large, the random channel vectors between the users and the BS become pair-wise orthogonal. Another major advantage of massive MIMO systems is that they facilitate us to reduce the transmitted power. On the uplink channel, reducing the transmit power of the user terminals will cut down the rates of their drained batteries (Marzetta, 2010; Rayi et al., 2016).
In this work, performance analysis of the uplink of noncooperative multi-cellular Time Division Duplexing systems has been presented. A realistic system model which accounts for imperfect channel estimation, antenna correlation, pilot contamination, and path loss is considered. Assuming that N and K are large, authors derive asymptotically tight approximations of the achievable rates with several linear detectors, i.e., Matched Filter (MF) and Minimum Mean-Square Error Detector (MMSE) in the UL.
In second part, the trade-off between spectral efficiency and energy efficiency is studied, in which imperfect CSI from uplink pilots from user to base station is used. In this analysis for different values of transmitted power from user, both spectral efficiency and energy efficiency will be derived to plot a curve. Then by increasing the number of base station antennas, the effect of increased base station antennas on trade-off curve is analyzed.
Approximation of achievable capacity in bits/S/Hz for both uplink with MF (Matched Filter) and MMSE (Minimum Mean Square Error) detectors and the results are computed.
Consider a multi-cellular, TDD system consisting of L > 1 cells with one BS and K UTs in each cell, where the BSs are equipped with N antennas, and the UTs have a single antenna. It is consider that all BSs and UTs are completely synchronized and run a TDD protocol with frequency reuse concept (Marzetta, 2010). Flat fading channel is considered for transmission.
The received signal vector for uplink signal can be described as (Hoydis et al., 2013),
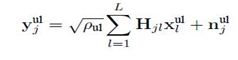
where Hjl = [hjl1 · · ·hjlK] ∈ CN×K, channel is hjlk ∈ CN for k user and base station j and cell is 1. The parameter xull =[xull1· · · xullK]T ~ CN (0, IK),where xulk is the transmit signal of K user and cell 1,noise vector is nulj ~ CN (0, IN), and uplink SNR is ρul > 0. The channel vectors hjlk are modelled as,
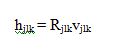
where Rjlk_=˜Rjlk ˜RHjlk ∈ CN×N are deterministic and vjlk ~ CN (0, IN) are independent fast-fading channel vectors.
A linear single-user detection, where the jthestimates the jm symbol Xul jmof UT m in its cell by computing the inner product between the received vector yulj and a linear filter rjm ∈ CN is considered. Two particular filters are of practical interest, namely the matched filter rMFjm and the MMSE detector rMMSEjm
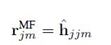
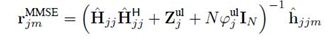
where, ρ jul> 0 and Zulj ∈ CN×N is an arbitrary Hermitian non-negative definite matrix. This formulation of rMMSEjm allows us to treat ρul j and Zul j as design parameters, which can be optimized. One can select for example ρulj = 1/ρulN and Zulj to be the co-variance matrix of the inter cell interference and the channel estimation errors.
Let us now consider the simplified channel model (Hoydis, et al., 2013).

where A ∈ CN×P is composed of P ≤ N columns of an arbitrary unitary N × N matrix, Vjl ∈ CP×K are standard complex Gaussian matrices and α ∈ (0, 1] is an intercell interference factor. Under this model, the total energy of the channel grows linearly with N and K, since E[ trHjjHHjj] = KN/P trAAH = KN. The inspiration following this channel model is two fold. Assume that the aperture of antenna increases with each additional antenna element. Thus, the captured energy by antenna increases proportional to N. For example, at a carrier frequency of 2.6 GHz (i.e., wavelength λ ≈ 12 cm), a 16 × 16 antenna array with λ/2-spacing would occupy an area of around 1m2 . Transmit power for uplink and downlink are assumed same, i.e.,ρul = ρdl = ρ, and that the precoding matrices Zdlj and Zulj are also equivalent. By dl ul considering the above conditions, performance of MF and BF can be described as below,
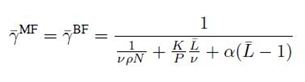

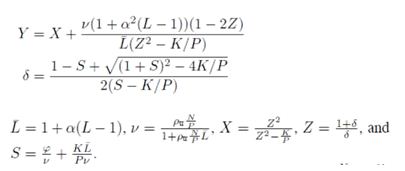
Here, the asymptotic SINR depends on the transmit SNR ρ through the term 1 /νρN . So, “ρN” is an effective SNR and is linearly increased with N.
Achievable approximate rate with MF and MMSE are given by,
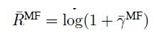
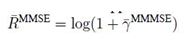
The energy efficiency can be defined as spectral efficiency divided by transmit power. Hence there is always trade-off between energy efficiency and spectral efficiency of a system.
Equation of spectral efficiency with MRC (Maximum Ratio Combining) detector (Nog, et al, 2013) is,
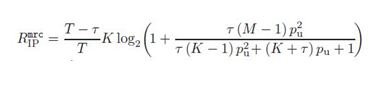
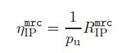
Numerical values used for analysis of mathematical equations of approximation of achievable rates in bits/S/Hz for MF and MMSE detector are presented in Table 1. The above equations are simulated in MATLAB and relative plots are derived. For trade-off analysis, the authors have derived equations of spectral efficiency for different values of number of base station antennas and different values of transmitted power. The number of users K was optimized jointly with pu and τ/T to maximize the energy efficiency for the given spectral efficiency. Any operating point on the curves can be obtained by appropriately selecting pu and optimizing with respect to K and τ/T.
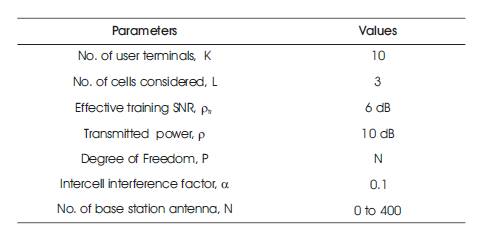
Table 1. Numerical Values used in Approximation of Achievable Rate with MF and MMSE Detector
Numerical values used for derivation of trade-off between spectral efficiency and energy efficiency are given in Table 2
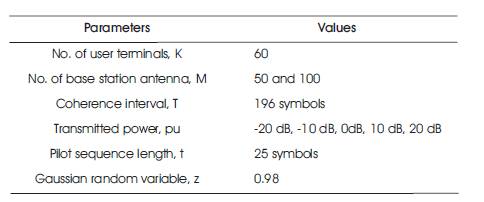
Table 2. Numerical Values used in Derivation of Trade Off between Spectral Efficiency and Energy Efficiency
It is concluded from plots of Figure 1 and Figure 2 that ergodic achievable rate versus number of base station antennas for MF (Matched Filter) detection (Figure 1) and MMSE (Minimum Mean Square Error) detection (Figure 2) that as number of antenna increases, achievable rate also increases and accordingly the authors select how many antennas are required to achieve required achievable rate. In Figure 3 from the comparison of achievable rate with MF and MMSE detection, it can be observed that by using same number of base station antennas, one can achieve higher ergodic achievable rate with MMSE detection compared to MF detection. Thus performance of MMSE detector is superior in terms of achievable rate compared to MF detector in massive MIMO system.
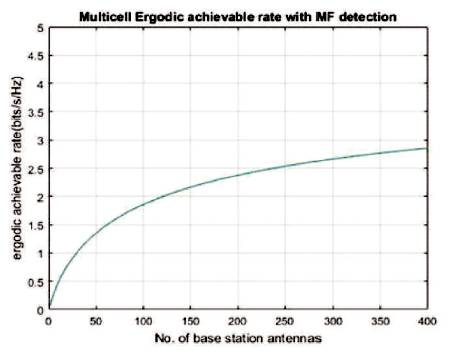
Figure 1. Plot of Multi Cell Ergodic Achievable Rate with MF Detection
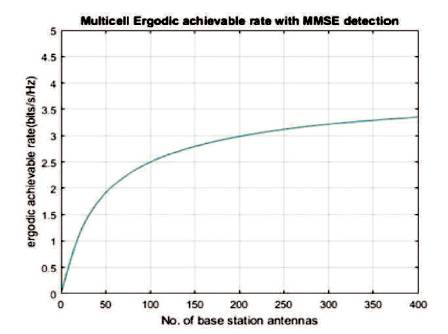
Figure 2. Plot of Multicell Ergodic Achievable Rate with MMSE Detection
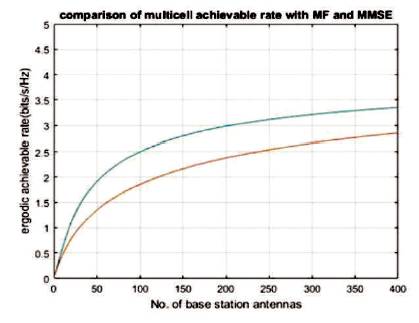
Figure 3. Plot of Comparison of Multicell Achievable Rate with MF and MMSE Detection
In Figure 4, Spectral Efficiency (SE) versus Energy Efficiency (EE), different values of EE and SE is obtained by varying transmit power from -20 dB, -10 dB, 0 dB, 10 dB, and 20 dB. As the transmit power is increased, SE is increasing at the cost of decreasing EE. Number of base station antennas (M) also impact SE and EE. In plot, it is observed that number of base station antenna M = 100, where both SE and EE is higher compared to derived for M = 50, but curve of graph remain same but shift upwards.
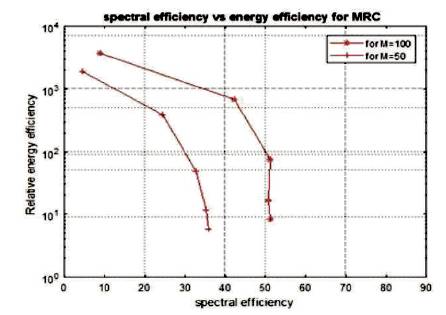
Figure 4. Plot of Spectral Efficiency Versus Energy Efficiency