Introduction
In the present scenario, the necessity for the storage and transmission of large numbers of high quality images is increasing, it is important to consider techniques for representing an image with less size. By eliminating redundant or unnecessary information from the digital image we can achieved better image compression. Image compressions techniques have been applied in several areas of image and video processing such as TV transmission, video conferencing, portable video telecommunication and mobile based web communication.
The choice of compression algorithm involves several conflicting considerations. These include degree of compression, speed of operation and size of compressed file versus quality of decompressed image. The digital image compression can be classified as lossless and lossy image compression. Lossless compression works by reducing the redundancy in the image. The decompressed image is an exact copy of the original, without any loss. The example of lossless compression algorithms includes Huffman Encoding. Lossy compression sacrifices exact reproduction of image for better compression. It removes redundancy and creates an approximation of the original image. The JPEG standard is currently the most popular method of lossy image compression. Fractal image compression is also a lossy image compression method [1].
The French mathematician Benoit B. Mandelbrot first coined the term fractal in 1975. He derived the word from the Latin fractus, which means "broken", or "irregular and fragmented". The Fractal image compression techniques were proposed by Barnsley et al. (1988) as a compression method [1] for binary images, and applied to gray-scale images [2,3].
Liu et al. (2005) implemented parallel fractal image compression. they included the iterated function system theory and reviews the different techniques that can be applied in parallelize the compression algorithm [4]. Ching et al. (2006) proposed fractal image compression technique is improved with TIES (Two pass Improved Encoding Scheme). Their proposed algorithm is a two-pass scheme, whereby the first-pass involves extracting the domain pool (as in the original FIC algorithm), and the second-pass involves extracted domain pool to achieve the maximum compression [5]. Wang et al (2006) developed a method on a Virtual Hexagonal Image Structure (VHS) by adopting Fisher's basic method on the traditional square image structure [6]. Chaurasia et al (2009) suggested many techniques at every step of process of fractal image compression [7]. Fang et al (2009) proposed a technique of parallel implementation of fractal image compression algorithm in Web service environment. An experimental results show, their technique can greatly reduce the compression time and achieve a high speed up at the same quality of decompressed image [8]. Vahdati et al (2009) proposed a new method to reduce the fractal encoding time based on computing the gray level difference and normal variance of domain and range blocks [9]. Hussain et al (2009) implemented and evaluated the performance of parallel fractal image compression strategy on cluster of workstations [10]. Hua Cao et al (2010, 11) are parallelly implemented fisher fractal coding algorithm and Jacquin fractal coding algorithm using Open MP program model. According to their experiment, results show that the speed-up ratio is more than four times compared with the original sequential program [11,12].
Fractal image compression is time consuming due to the search of the matching between range and domain blocks. In order to improve this compression method, authors proposed a fast method for reducing the computational complexity of fractal encoding by reducing the size of the domain pool. Genetic algorithm, neural network and other soft computing based parallel computing have also been used to improve the performance of fractal image compression system. [13,14].
In the present paper, fractal image encoding algorithm has been parallely implemented for 256x256, 512X512 grayscale images using Java parallel processing tool (JPPF) to reduce the encoding time.
1. Fractal Image Compression
Fractal image compression has received considerable attention because of its use of the self-similarity in images. The innovation that had not been used previously in the field of image compression. A fractal is a rough or fragmented geometric shape that can be sub divided in parts, each of which is (at least approximately) a reduced-size copy of the whole.
1.1. Fractal Image Coding
The main theory of fractal image coding is based on iterated function system, attractor theorem and Collage theorem. Fractal coding process is quite complicated but decoding process is very simple. The overall process of fractal image encoding includes four levels of decision-making. A wide variety of methods have been suggested by the researcher for every level. The detail of levels and methods used in different levels are shown below:
- Partition of image and form a range blocks.
- Selection of a set of domain blocks. .
- Selection of a class of transforms applied to the domain block. .
- Search of most suitable domain block to form particular range block. .
1.1.1. Partition of image and form a range blocks
In FIC system the first level is an image partition for the image range formation. A wide variety of partition scheme have been developed by different researchers. Fixed size square blocks are the simplest possible partition [2]. Quad-tree partitions and Horizontal-Vertical (HV) partitions are adaptive scheme for block size partition that large blocks are assigned for low detail region and small blocks for significant detail region. Other techniques are Polygonal blocks of different shapes and Irregular partitions [7].
1.1.2. Selection of a set of domain blocks
Domain pool selection is the second level of fractal image compression. This choice depends on the type of partition scheme used. The domain pool in fractal encoding is similar to the codebook in Vector Quantization (VQ), Global domain pool was the first and simplest type of domain pool [5].
1.1.3. Selection of a class of transforms applied to the domain block
Transforms selection is the most crucial part of a fractal-encoding scheme. These transforms are applied on domain blocks to form range blocks and determines the convergence properties of decoding. The partition scheme used and the type of domain pool used restrict the choice of transforms. Since domain blocks are mapped into range blocks using these transforms, all the transforms are used for this purpose should be contractive in nature. Each of transform can skew, stretch, rotate, scale and translate any domain image. The general form of transformations suggested by Jacquin is given as sum of elementary block transformation or isometric transformation. An affine mapping scheme is as well applicable on nonrectangular partitions. Figure1 shows Domain to Range Block transformation, here Di is domain block and (Di) transformed domain block equivalent to range block [2].
1.1.4. Search of most suitable domain block to form particular range block
After selection of suitable partitioning, domain-pool and transformation, fourth step of fractal encoding process is the search of suitable candidate from all available domain blocks to encode any particular range block. This step of fractal image compression is computationally very expensive, because it requires a large number of domain-range comparisons.
A Fractal Image encoding process is shown in Figure 2 with four different levels.
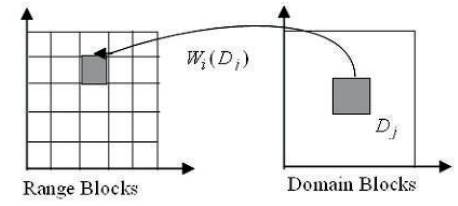
Figure 1. Domain-Range Block Transformation
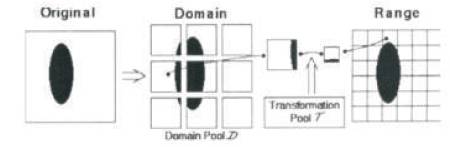
Figure 2. Fractal Image Encoding Process
1.2. Iterated Function Systems
An iterated function system is a collection of affine transformations [2] that map a plane to it. This collection defines a map W given by
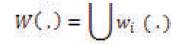
1.3 Contractive Mapping Fixed-Point Theorem
The contractive mapping fixed-point theorem states that if we are given a contractive map W, then there is an attractor denoted by xw with the following properties:
- Applying the affine transformation to the attractor yields the attractor. This attractor xw is called the fixed point of W, i.e.
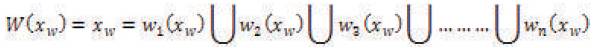
- Given any input image, if we run the affine transformations sufficiently large number of times, the resulting image is the attractor, i.e.
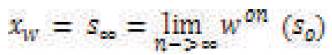
2. Proposed Parallel Architecture
A large number of different strategies have been developed for parallelization of the encoding stage of fractal image compression algorithm. The interest of using parallelization on Fractal based image compression from high computational cost is required in encoding process. We can individualize several types of parallelism at different levels of granularity, being granularity is a measure given by the ratio between the computing and the communication times involved in the parallel algorithm.
In the present work 8-bit grey scale 2N x 2N image is to be compressed. Firstly, N x N image is partitioned into n x n Range Blocks. Then Range Blocks are distributed on Multiple of four Processing Elements (PE's). Approximate (N x N) / (n x n x 4) ranges are to be executed on each PE. It reduces the encoding time by the factor of four. Affine transformations are used on 2n x 2n scaled domain blocks.
The scaling (s) and offset (o) factors and Mean Square Error (MSE) are formalized shown below for matching domain block and range block [3]:
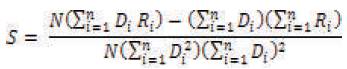
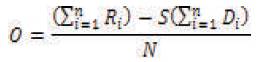
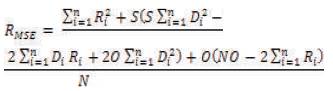
2.1 Data Flow Diagram of Proposed Image Compression
The Proposed fractal encoding algorithm is pictorially represented on Figure 3. This algorithm is executed in serial as well as parallel manner. The description of the data flow diagram as follows:
- Divide the whole gray scale image into 4 x 4 size blocks which are called range and divide all ranges into n number of equal parts then distribute each part to n (i.e. 2, 4, or 8) number of computers.
- Again divide the image to 8 x 8 size blocks which are called domains and distribute all the domains to each computer.
- For each range on n computers search the best matched domain for that range by the algorithm described in the sections 2.2 and 2.2 and store the resultant information into a file, which is called fractal code file, with extension FIF.
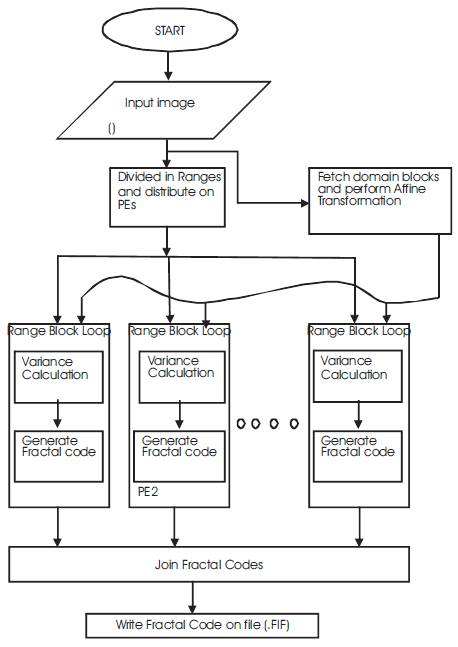
Figure 3. Data Flow Diagram of Proposed Fractal Image Compression
2.2. Fractal Image Encoding Algorithm
Begin:-
Input: I = Read, NxN square grey scale image. (N= 256x256, 512x512)
Step1: Image I is divided in nxn non-overlapping range blocks [R],
Step2: Divide image I, mxm overlapped domain blocks (D) and distribute it to all Pes.
Step3: Divide R into i ( i = 2, 4, 8) equal parts and distribute each part to all Pes.
Step4: Perform following for each Ri block on PEs simultaneously:
- Take a Dj from domain pool;
- Dsj =: Scaling _Operations(Dj);
- Compare Ri with Dsj by performing affine transformation.
- Calculate scale Si, offset Oi and MSE difference Rmse by using equation (4), (5)and(6).
- Repeat steps i) to iv) for all possible overlapped domains.
Step5: Select that domain out of D domains, which has the smallest MSE difference (called best matched domain) with range and store its pixel position in image, Affine Transformation wk, MSE error (Rmse), scaling factor (Si) and offset factor (Oi).
Step6: Repeat steps 4 to 5 until all ranges have covered.
Step7: Store all the above information of image called Fractal Code into a file called Fractal Image File (with extension FIF).
End;
2.3. Algorithm used for decoding
The fractal encoded file is not an image file and needs to be decoded in order to see the reconstructed image. A method for decoding the encoded file is thus necessary. An algorithm used to decode the encoded image is now described below, which was given by A. Jacquin and mentioned in [2]:
Begin:
Step1 Read .FIF file and perform following steps:
- Repeat steps i to iv for all ranges (R):
- Read domain coordinates Xi, Yi for Ri range from FIF file and read mxm domain block from Xi, Yi position of initial image.
- Scale mxm size domain to nxn range size.
- Apply affine transform Wi; adjust its brightness and luminescence by Si and Oi factors by reading FIF file.
- Modify the initial image by drawing this block to ith range block.
Step2 Goto Step-1, 10 times.
End;
In the present paper 256x256 and 512x512 gray scale images have been compressed on SPMD (Single Program Multiple Data) based parallel architecture over single, 2, 4, and 8 PE's respectively.
3. Java Parallel Processing Framework (JPPF)
JPPF is an open source Grid Computing platform written in Java, that makes it easy to run applications in parallel, and speed up their execution by orders of magnitude. “Write once, deploy once, execute everywhere “, that is main motivation of JPPF.
3.1 Architecture of JPPF
The Java Parallel Processing Framework has a 3-tiered architecture, made of 3 distinct layers:
3.1.1 Client layer: Provides an API and communication tools to use the framework to submit tasks, to execute in parallel.
3.1.2 Service layer: Responsible for the communication between with the clients and the nodes, along with the management of the execution queue, the load-balancing and recovery features, and the dynamic loading of both framework and application classes onto the appropriate nodes.
3.1.3 Execution layer: These are the nodes. They execute individual tasks, return the execution results, and dynamically request, from the JPPF driver, the code they need to execute the client tasks. Figure 4(a) illustrates architecture of JPPF [15].
JPPF can be implemented COWS (cluster of work station) to include many servers communicating together in a peer-to-peer topology that represented in Figure 4(b). In this topology, each server is seen by its peers as a node, and observes its peers as clients. There are a number of major advantages to this design. In the present work, JPPF is used as parallel processing tool for implementing the Fractal encoding.
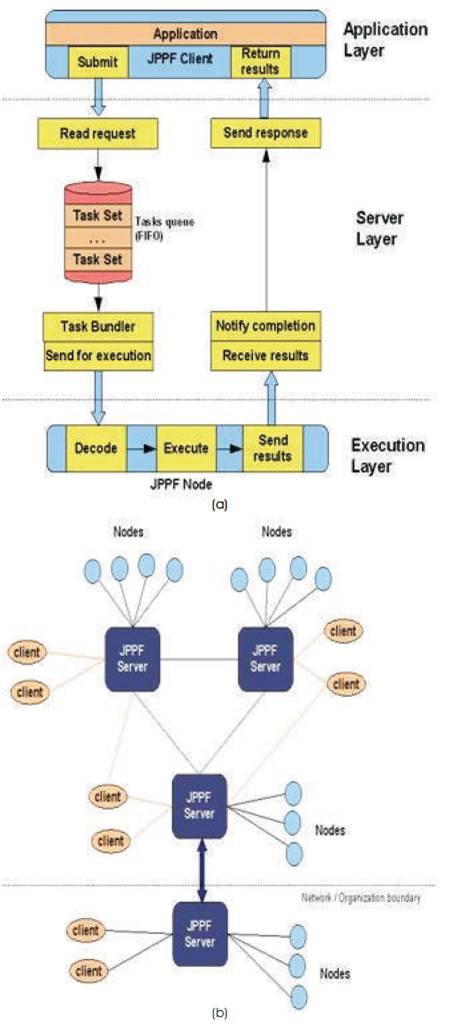
Figure 4 (a). Architecture of JPPF, (b). Topology
4. Experimental Results
The proposed parallel Fractal image compression algorithm has been implemented on Intel Pentium Dual CPU, 1.6 GHz, 1GB RAM personal computer as a server and Pentium D-CPU, 2.8GHz, 512MB RAM personal computers as a node using Java Parallel Processing Framework with Linux platform. The proposed algorithm has been tested on five 255x255 grayscale images and six 512x512 grayscale images on single computer, 2 computers, 4 computers and on 8 computers one by one and the following results are obtained:
4.1. Experimental Results on 256x256 grayscale images
Figure 5 shows the original image and after decompression reconstructed image. That is approximate to the original one. Table 1 show the % time saving and speed-up obtained by running the algorithm of section 3.2 parallelly on 2, 4, and 8 nodes over single node respectively for 256x256 size images. Figure 6 shows the execution on different node for various images. Table 2 shows Compression Ratio, Decompression Time, Mean Square Error and PSNR values obtained from proposed decompression algorithm by the retrieving of 256x256 Grayscale Image. Figure 7 and 8 show the graphs of % time saving and speed-up obtained for 256x256 images respectively.
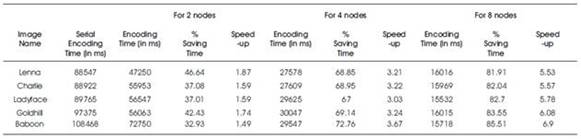
Table 1. Encoding Time (msec) obtained in the execution of FIC in sequential and parallel manner of various 256x256 gray scale images
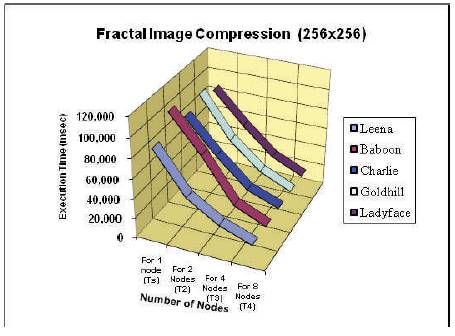
Figure 6. Plot of number of nodes (CPU's) vs encoding time obtained by the parallel FIC algorithm for various Images
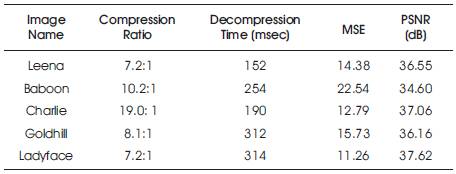
Table 2. Compression Ratio, Decompression Time, Mean Square Error and PSNR values obtained from proposed decompression algorithm by the retrieving of 256x256 Grayscale Image
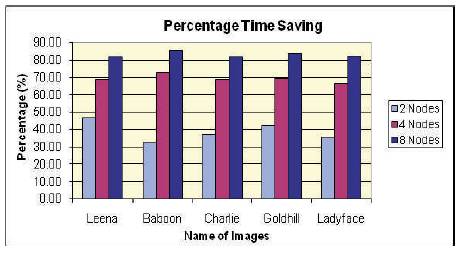
Figure 7. Percentage time saving for parallel execution of proposed FIC algorithm of different 256x256 images
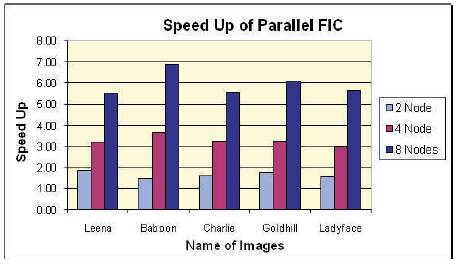
Figure 8. Speed Up for parallel execution of proposed FIC algorithm of different 256x256 images
Figure 9 shows the 512x512 original images and after decompression reconstructed image. Table 3 shows the % time saving and speed-up obtained by running the algorithm of section 3.2 parallelly on 2, 4, and 8 nodes over single node respectively for 512x512 size images. Figure 10 shows the execution on different node for various images. Figure 11 and 12 represent graphs of % time saving and speed-up obtained for 512x512 images compression respectively.
It is observed from the tables and figures of experimental results that when the encoding is done on single, 2, 4, and 8 nodes respectively from Figure 6 and 9, the execution time is decreasing almost linearly. In the Figure 7,8,10,12 the % increment in time saving(speed up) from 2 nodes to 4 nodes is more than the % increment in time saving from 4 nodes to 8 nodes (i.e. the relation of % saving time and nodes tends to become plateau as the number of node are increased), Table 2 and 4 shows the Compression Ratio, Decompression Time, Mean Square Error and PSNR values obtained from the proposed decompression algorithm by the retrieving of 256X256, 512x512 Grayscale Image. Here, we observed decompression is very less compared to compression time.
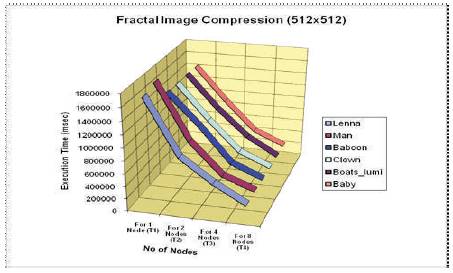
Figure 10. Plot of number of nodes (CPU's) vs encoding time obtained by the parallel FIC algorithm for various Images
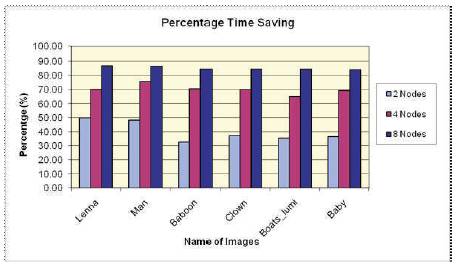
Figure 11. Percentage time saving for parallel execution of proposed FIC algorithm of different 512x512 images
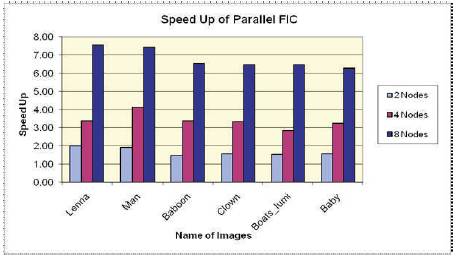
Figure 12. Speed Up for parallel execution of proposed FIC algorithm of different 512x512 images
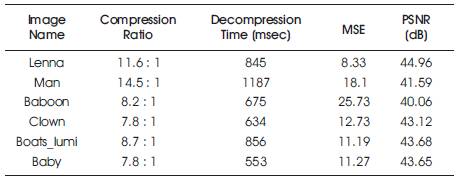
Table 4. Compression Ratio, Decompression Time, Mean Square Error and PSNR values obtained from the proposed decompression algorithm by the retrieving of 512x512 Grayscale Image
Conclusion
The present work is an endeavor to develop and implement an algorithm. A novel algorithm of parallelization of fractal image compression using JPPF has been developed and run on single, 2, 4, and 8 computers one by one using JPPF. It was run for five 256x256 and six 512x512 different grayscale images then; we obtained better time saving and speedup. It has also been cleared that the very complex time taken algorithms are executing in low cost and high speed. No expensive hardware (like SIMD, MIMD, graphics board etc.) or software is required for implementation. For implementation we require a few numbers of computers connected through LAN and free available open source parallelization tool JPPF.