In Machine Learning community, and in Data Mining works, Classification has its own importance. Classification is an important part and the research application field in the data mining [1]. With ever-growing volumes of operational data, many organizations have started to apply data-mining techniques to mine their data for novel, valuable information that can be used to support their decision making [2]. Organizations make extensive use of data mining techniques in order to define meaningful and predictable relationships between objects [3]. Decision tree learning is one of the most widely used and practical methods for inductive inference [4]. This paper presents an updated survey of various decision tree algorithms in machine learning. It also describes the applicability of the decision tree algorithm on real-world data.

The rest of this paper is organized as follows. In Section 1, the authors presented the basics of data mining and classification. In Section 2, they present the imbalanced data-sets problem, and in Section 3, they present the various evaluation criteria's used for class imbalanced learning. In Section 6, we presented updated survive of class imbalance learning methods. Finally, in Section 7, we make our concluding remarks.

Data Mining is the analysis of (often large) observational data sets to find unsuspected relationships and to summarize the data in novel ways that are both understandable and useful to the owner [5]. There are many different data mining functionalities. A brief definition of each of these functionalities is now presented. The definitions are directly collated from [6]. Data characterization is the summarization of the general characteristics or features of a target class of data. Data Discrimination, on the other hand, is a comparison of the general features of target class data objects with the general features of objects from one or a set of contrasting classes. Association analysis is the discovery of association rules showing attribute value conditions that occur frequently together in a given set of data.

Classification is an important application area for data mining. Classification is the process of finding a set of models (or functions) that describe and distinguish data classes or concepts, for the purpose of being able to use the model to predict the class of objects whose class label is unknown. The derived model can be represented in various forms, such as classification rules, decision trees, mathematical formulae, or neural networks. Unlike classification and prediction, which analyze class-labeled data objects, clustering analyzes data objects without consulting a known class label.

Outlier Analysis attempts to find outliers or anomalies in data. A detailed discussion of these various functionalities can be found in [6]. Even an overview of the representative algorithms developed for knowledge discovery is beyond the scope of this paper. The interested person is directed to the many books which amply cover this in detail [5], [6].

Learning how to classify objects to one of a pre-specified set of categories or classes is a characteristic of intelligence that has been of keen interest to researchers in psychology and computer science. Identifying the common -core characteristics of a set of objects that are representative of their class is of enormous use in focusing the attention of a person or computer program. For example, to determine whether an animal is a zebra, people know to look for stripes rather than examine its tail or ears. Thus, stripes figure strongly in our concept (generalization) of zebras. Of course stripes alone are not sufficient to form a class description for zebras as tigers have them also, but they are certainly one of the important characteristics. The ability to perform classification and to be able to learn to classify gives people and computer programs the power to make decisions. The efficacy of these decisions is affected by performance on the classification task.

In machine learning, the classification task described above is commonly referred to as supervised learning. In supervised learning there is a specified set of classes, and example objects are labeled with the appropriate class (using the example above, the program is told what a zebra is and what is not). The goal is to generalize (form class descriptions) from the training objects that will enable novel objects to be identified as belonging to one of the classes. In contrast to supervise learning is unsupervised learning. In this case the program is not told which objects are zebras. Often the goal in unsupervised learning is to decide which objects should be grouped together—in other words, the learner forms the classes itself. Of course, the success of classification learning is heavily dependent on the quality of the data provided for training—a learner has only the input to learn from. If the data is inadequate or irrelevant then the concept descriptions will reflect this and misclassification will result when they are applied to new data.

A decision tree is a tree data structure with the following properties:

• Each leaf is labeled with the name of a class;
• The root and each internal node (called a decision node) are labeled with the name of an attribute;
• Every internal node has a set of at least two children, where the branches to the children are labeled with disjoint values or sets of values of that node's attribute such that the union of these constitutes the set of all possible values for that attribute. Thus, the labels on the arcs leaving a parent node form a partition of the set of legal values for the parent's attribute.

A decision tree can be used to classify a case by starting at the root of the tree and moving through it until a leaf is reached [7]. At each decision node, the case's outcome for the test at the node is determined and attention shifts to the root of the sub tree corresponding to this outcome. When this process finally (and inevitably) leads to a leaf, the class of the case is predicted to be that labeled at the leaf.

Every successful decision tree algorithm (e.g. CART [8] , ID3 [9] , C4.5 [7]) is an elegantly simple greedy algorithm:

I.Pick as the root of the tree the attribute whose values best separate the training set into subsets (the best partition is one where all elements in each subset belong to the same class);

ii.Repeat step (i) recursively for each child node until a stopping criterion is met.

Examples of stopping criteria are:

• Every subset contains training examples of only one class;
• The depth of the tree reaches a predefined threshold;
• Lower bound on the number of elements that must be in a set in order for that set to be partitioned further is reached (CART [8] , C4.5 [7]).

The dominating operation in building decision trees is the gathering of histograms on attribute values. As mentioned earlier, all paths from a parent to its children partition the relation horizontally into disjoint subsets. Histograms have to be built for each subset, on each attribute, and for each class individually.

A dataset is class imbalanced if the classification categories are not approximately equally represented. The level of imbalance (ratio of size of the majority class to minority class) can be as huge as 1:99 [10]. It is noteworthy that class imbalance is emerging as an important issue in designing classifiers [11], [12], [13]. Furthermore, the class with the lowest number of instances is usually the class of interest from the point of view of the learning task [14]. This problem is of great interest because it turns up in many real-world classification problems, such as remote-sensing [15], pollution detection [16], risk management [17], fraud detection [18], and especially medical diagnosis [19]–[22].

There exist techniques to develop better performing classifiers with imbalanced datasets, which are generally called Class Imbalance Learning (CIL) methods. These methods can be broadly divided into two categories, namely, external methods and internal methods. External methods involve preprocessing of training datasets in order to make them balanced, while internal methods deal with modifications of the learning algorithms in order to reduce their sensitiveness to class imbalance [23]. The main advantage of external methods as previously pointed out, is that they are independent of the underlying classifier. In this paper, we are laying more stress to propose an external CIL method for solving the class imbalance problem.

Whenever a class in a classification task is underrepresented (i.e., has a lower prior probability) compared to other classes, we consider the data as imbalanced [24], [25]. The main problem in imbalanced data is that the majority classes that are represented by large numbers of patterns rule the classifier decision boundaries at the expense of the minority classes that are represented by small numbers of patterns. This leads to high and low accuracies in classifying the majority and minority classes, respectively, which do not necessarily reflect the true difficulty in classifying these classes. Most common solutions to this problem balance the number of patterns in the minority or majority classes.

Either way, balancing the data has been found to alleviate the problem of imbalanced data and enhance accuracy [24], [25], [26]. Data balancing is performed by, e.g., oversampling patterns of minority classes either randomly or from areas close to the decision boundaries. Interestingly, random oversampling is found comparable to more sophisticated oversampling methods [26] . Alternatively, undersampling is performed on majority classes either randomly or from areas far away from the decision boundaries. We note that random undersampling may remove significant patterns and random oversampling may lead to overfitting, so random sampling should be performed with care. We also note that, usually, oversampling of minority classes is more accurate than undersampling of majority classes [26] .

Resampling techniques can be categorized into three groups. Undersampling methods, which create a subset of the original data-set by eliminating instances (usually majority class instances); oversampling methods, which create a superset of the original data-set by replicating some instances or creating new instances from existing ones; and finally, hybrids methods that combine both sampling methods. Among these categories, there exist several different proposals; from this point, we only center our attention in those that have been used in under sampling.

• Random undersampling: It is a nonheuristic methodthat aims to balance class distribution through the random elimination of majority class examples. Its major drawback is that it can discard potentially useful data, which could be important for the induction process.
• Random oversampling: In the same way as random oversampling, it tries to balance class distribution, but in this case, randomly replicating minority class instances. Several authors agree that this method can increase the likelihood of occurring overfitting, since it makes exact copies of existing instances.
• Hybrid Methods:In this hybrid method both undersampling and oversampling will be applied for the datasets so as to make it a balance dataset.

The bottom line is that when studying problems with imbalanced data, using the classifiers produced by standard machine learning algorithms without adjusting the output threshold may well be a critical mistake. This skewness towards minority class (positive) generally causes the generation of a high number of false-negative predictions, which lower the model's performance on the positive class compared with the performance on the negative (majority) class. A comprehensive review of different CIL methods can be found in [27]. The following two sections briefly discuss the external-imbalance and internal-imbalance learning methods.

The external methods are independent from the learning algorithm being used, and they involve preprocessing of the training datasets to balance them before training the classifiers. Different resampling methods, such as random and focused oversampling and undersampling, fall into to this category. In random undersampling, the majority-class examples are removed randomly, until a particular class ratio is met [28] . In random oversampling, the minority-class examples are randomly duplicated, until a particular class ratio is met [27]. Synthetic Minority Oversampling TEchnique (SMOTE) [29] is an oversampling method, where new synthetic examples are generated in the neighborhood of the existing minority-class examples rather than directly duplicating them. In addition, several informed sampling methods have been introduced in [30].

This section follow a design decomposition approach to systematically analyze the different unbalanced domains.

To assess the classification results we count the number of True Positive (TP), True Negative (TN), False Positive (FP) (actually negative, but classified as positive) and False Negative (FN) (actually positive, but classified as negative) examples. It is now well known that error rate is not an appropriate evaluation criterion when there is class imbalance or unequal costs. In this paper, we use AUC, Precision, F-measure, TP Rate and TN Rate as performance evaluation measures.

Let us define a few well known and widely used measures for C4.5 [7] as the baseline classifier with the most popular machine learning publicly available datasets at Irvine [31]:

The Area Under Curve (AUC) measure is computed by,

[1]

The Precision measure is computed by,

[2]

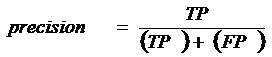
The F-measure Value is computed by,

[3]

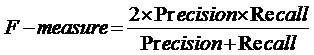
The True Positive Rate measure is computed by,

[4]

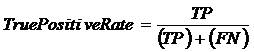
The True Negative Rate measure is computed by,

[5]

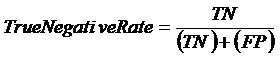
Table I summarizes the benchmark datasets used in almost all the recent studies conducted on class imbalance learning. The details of the datasets are given in Table I. For each data set, the number of examples (#Ex.), number of attributes (#Atts.), class name of each class (minority and majority), the percentage of examples of each class and the IR is given. This table is ordered by the IR, from low to high imbalanced data sets. The complete details regarding all the datasets can be obtained from Victoria Lópezet al. [38] and Machine Learning Repository [52].

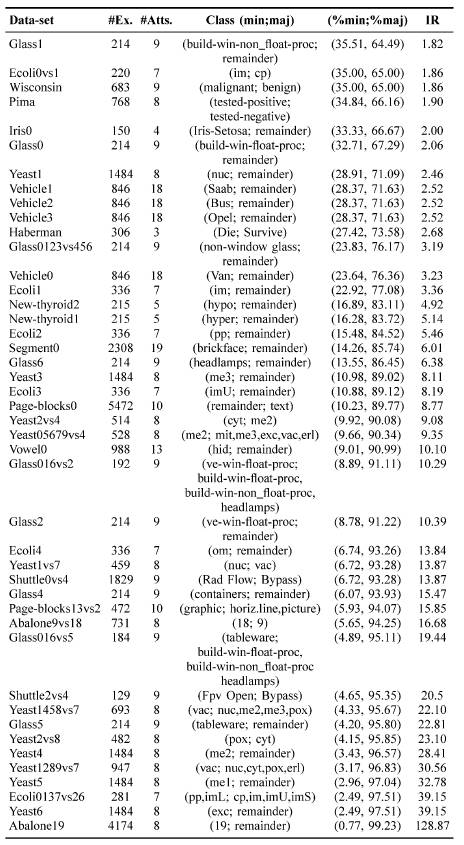
Table 1. Summary Of Benchmark Imbalanced Datasets

Currently, the research in class imbalance learning mainly focuses on the integration of imbalance class learning with other AI techniques. How to integrate the class imbalance learning with other new techniques is one of the hottest topics in class imbalance learning research. There are some of the recent research directions for class imbalance learning as follows:

T. Jo et al. [32] have proposed a clustering-based sampling method for handling class imbalance problem, while S. Zouet al. [33] have proposed a genetic algorithm based sampling method. Jinguha Wang et al. [34] have suggested a method for extracting minimum positive and maximum negative features (in terms of absolute value) for imbalanced binary classification is proposed. They have developed two models to yield the feature extractors. Model 1 first generates a set of candidate extractors that can minimize the positive features to be zero, and then chooses the ones among these candidates that can maximize the negative features. Model 2 first generates a set of candidate extractors that can maximize the negative features, and then chooses the ones that can minimize the positive features. Compared with the traditional feature extraction methods and classifiers, the proposed models are less likely affected by the imbalance of the dataset. Iain Brown et al. [35] have explored the suitability of gradient boosting, least square support vector machines and random forests for imbalanced credit scoring data sets such as loan default prediction. They progressively increase class imbalance in each of these data sets by randomly undersampling the minority class of defaulters, so as to identify to what extent the predictive power of the respective techniques is adversely affected. They have given the suggestion for applying the random forest and gradient boosting classifiers for better performance. Salvador Garcı´aet al. [36] have used evolutionary technique to solve the class imbalance problem. They proposed a method belonging to the family of the nested generalized exemplar that accomplishes learning by storing objects in Euclidean n-space. Classification of new data is performed by computing their distance to the nearest generalized exemplar. The method is optimized by the selection of the most suitable generalized exemplars based on evolutionary algorithms.

Jin Xiao et al. [37] have proposed a Dynamic Classifier Ensemble method for Imbalanced Data (DCEID) by combining ensemble learning with cost-sensitive learning. In this for each test instance, it can adaptively select out the more appropriate one from the two kinds of dynamic ensemble approach: Dynamic Classifier Selection (DCS) and Dynamic Ensemble Selection (DES). Meanwhile, new cost-sensitive selection criteria for DCS and DES are constructed respectively to improve the classification ability for imbalanced data. Victoria Lópezet al. [38] have analyzed the performance of data level proposals against algorithm level proposals focusing in cost-sensitive models and versus a hybrid procedure that combines those two approaches. They also lead to a point of discussion about the data intrinsic characteristics of the imbalanced classification problem which will help to follow new paths that can lead to the improvement of current models mainly focusing on class overlap and dataset shift in imbalanced classification.

Yang Yong [39] has proposed one kind minority kind of sample sampling method based on the K-means cluster and the genetic algorithm. They used K-means algorithm to cluster and group the minority kind of sample, and in each cluster they use the genetic algorithm to gain the new sample and to carry on the valid confirmation. Chris Seiffertet al. [40] have examined a new hybrid sampling/boosting algorithm, called RUSBoost from its individual component AdaBoost and SMOTEBoost, which is another algorithm that combines boosting and data sampling for learning from skewed training data. V. Garcia et al.[41] have investigated the influence of both the imbalance ratio and the classifier on the performance of several resampling strategies to deal with imbalanced data sets. The study focuses on evaluating how learning is affected when different resampling algorithms transform the originally imbalanced data into artificially balanced class distributions.

Table 2 recent algorithmic advances in class imbalance learning available in the literature. Obviously, there are many other algorithms which are not included in this table. Nevertheless most of these algorithms are variation of the algorithmic framework given in Section 2 and 3. A profound comparison of the above algorithms and many others can be gathered from the references list.

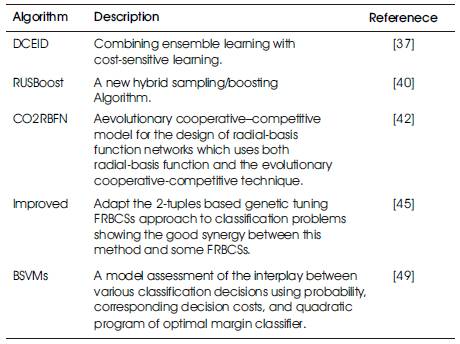
Table 2. Recent Advances in Class Imbalance Learning

María Dolores Pérez-Godoy et al. [42] have proposed CO2RBFN, a evolutionary Cooperative–Competitive model for the design of Radial-basis Function Networks which uses both radial-basis function and the evolutionary Cooperative–Competitive technique on imbalanced domains. CO2RBFN follows the evolutionary cooperative–competitive strategy, where each individual of the population represents an RBF (Gaussian function will be considered as RBF) and the entire population is responsible for the definite solution. This paradigm provides a framework where an individual of the population represents only a part of the solution, competing to survive (since it will be eliminated if its performance is poor) but at the same time cooperating in order to build the whole RBFN, which adequately represents the knowledge about the problem and achieves good generalization for new patterns.

Der-Chiang Li et al.[43] have suggested a strategy which over-samples the minority class and under-samples the majority one to balance the datasets. For the majority class, they buildup the Gaussian type fuzzy membership function and a-cut to reduce the data size; for the minority class, they used the mega-trend diffusion membership function to generate virtual samples for the class. Furthermore, after balancing the data size of classes, they extended the data attribute dimension into a higher dimension space using classification related information to enhance the classification accuracy. Enhong Cheet al.[44] have described a unique approach to improve text categorization under class imbalance by exploiting the semantic context in text documents. Specifically, they generate new samples of rare classes (categories with relatively small amount of training data) by using global semantic information of classes represented by probabilistic topic models. In this way, the numbers of samples in different categories can become more balanced and the performance of text categorization can be improved using this transformed data set. Indeed, this method is different from traditional re-sampling methods, which try to balance the number of documents in different classes by re-sampling the documents in rare classes. Such re-sampling methods can cause overfitting. Another benefit of this approach is the effective handling of noisy samples. Since all the new samples are generated by topic models, the impact of noisy samples is dramatically reduced.

Alberto Fernándezet al. [45] have proposed an improved version of Fuzzy Rule Based Classification Systems (FRBCSs) in the framework of imbalanced data-sets by means of a tuning step. Specifically, they adapt the 2-tuples based genetic tuning approach to classification problems showing the good synergy between this method and some FRBCSs. The proposed algorithm uses two learning methods in order to generate the RB for the FRBCS. The first one is the method proposed in [46] , that they have named the Chi et al.'s rule generation. The second approach is defined by Ishibuchi and Yamamoto in [47] and it consists of a Fuzzy Hybrid Genetic Based Machine Learning (FH-GBML) algorithm.

J. Burezet al.[48] have investigated how they can better handle class imbalance in churn prediction. Using more appropriate evaluation metrics (AUC, lift), they investigated the increase in performance of sampling (both random and advanced under-sampling) and two specific modeling techniques (gradient boosting and weighted random forests) compared to some standard modeling techniques. They have advised weighted random forests, as a cost-sensitive learner, performs significantly better compared to random forests.

Che-Chang Hsu et al. [49] have proposed a method with a model assessment of the interplay between various classification decisions using probability, corresponding decision costs, and quadratic program of optimal margin classifier called: Bayesian Support Vector Machines (BSVMs) learning strategy. The purpose of their learning method is to lead an attractive pragmatic expansion scheme of the Bayesian approach to assess how well it is aligned with the class imbalance problem. In the framework, they did modify in the objects and conditions of primal problem to reproduce an appropriate learning rule for an observation sample.

In [50] Alberto Fernándezet al. have proposed to work with fuzzy rule based classification systems using a preprocessing step in order to deal with the class imbalance. Their aim is to analyze the behavior of fuzzy rule based classification systems in the framework of imbalanced data-sets by means of the application of an adaptive inference system with parametric conjunction operators. Jordan M. Malofet al.[51] have empirically investigates how class imbalance in the available set of training cases can impact the performance of the resulting classifier as well as properties of the selected set. In this K-Nearest Neighbor (k-NN) classifier is used which is a well-known classifier and has been used in numerous case-based classification studies of imbalance datasets.

In this paper, the state of the art methodologies to deal with class imbalance problem has been reviewed. This issue hinders the performance of standard classifier learning algorithms that assume relatively balanced class distributions, and classic ensemble learning algorithms are not an exception. In recent years, several methodologies integrating solutions to enhance the induced classifiers in the presence of class imbalance by the usage of evolutionary techniques have been presented. However, there was a lack of framework where each one of them could be classified; for this reason, a taxonomy where they can be placed has been taken as our future work. Finally, we have concluded that intelligence based algorithms are the need of the hour for improving the results that are obtained by the usage of data preprocessing techniques and training a single classifier.