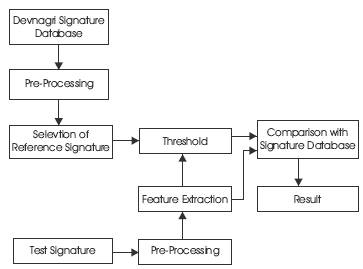
Figure 1. Simplified workflow for a typical Signature Recognition System
Development of a Character recognition system for Devnagari is difficult because (i) there are about 350 basic, modified (“matra”) and compound character shapes in the script and (ii) the characters in words are topologically connected. Here focus is on the recognition of offline handwritten Devnagari characters that can be used in common applications like bank cheques, commercial forms, government records, bill processing systems, Postcode Recognition, Signature Verification, passport readers, offline document recognition generated by the expanding technological society. Challenges in handwritten signature recognition lie in the variation and distortion of handwritten signature or script since different people may use different style of handwriting, and direction to draw the same shape of any Devnagari character. This overview describes the nature of handwritten language, how it is translated into electronic data, and the basic concepts behind written language recognition algorithms. Handwritten Devnagari signatures are imprecise in nature as their corners are not always sharp, lines are not perfectly straight, and curves are not necessarily smooth, unlikely the printed character. An approach using Artificial Neural Network is considered for recognition of Handwritten Devnagari Signature. The learning process inherent in Neural Networks (NN) can be applied to the process of verifying handwritten signatures that are electronically captured via a stylus. This paper presents a method for verifying handwritten signatures by using NN architecture. Various static (e.g., area covered, number of elements, height, slant, etc.) (Plamondon & Srihari, 2000) and dynamic (e.g., velocity, pen tip pressure, etc.) signature features are extracted and used to train the NN (Daramola & Ibiyemi, 2010). Several Network topologies are tested and their accuracy is compared. Although the verification process can be thought to as a monolith component, it is recommended to divide it into loosely coupled phases (like preprocessing, feature extraction, feature matching, feature comparison and classification) allowing us to gain a better control over the precision of different components. This paper focuses on classification, the last phase in the process, covering some of the most important general approaches in the field. Each approach is evaluated for applicability in signature verification, identifying their strength and weaknesses. It is shown, that some of these weak points are common between the different approaches and can partially be eliminated with our proposed solutions. To demonstrate this, several local features are introduced and compared using different classification approaches.
The proposed system for Devnagari signature recognition consists of 3 main phases. First they extract some features from the images of particular signature, then they compare them and finally, they use some kind of classifier to recognize the signature [Srihari & Kalera, 2004]. This paper concentrates on the final phase of signature recognition. In this paper a complete neural network based classification method is introduced to demonstrate, how some of the limitations of off-line signature recognition system can be overcome. Finally experimental results are presented and used to evaluate the goodness of several different features. Concentrated efforts at applying NNs to Handwritten Devnagari Signature Recognition (HDSR) have been undertaken for over a decade with varying degrees of success [Arica, Fatos & Vural, May 2001].
A method for HDSR using NN architecture is presented in this paper. Various static features (e.g., height, length of signature, number of breaks in signature etc.) are extracted and used to train the NN. Several Network topologies are tested and their accuracy is compared. Hindi is widely used language in south Asian region which is written in Devanagari script. Hindi is also official language of India. The words in Devanagari script are not written in cursive manner but there are some alphabets which some individuals write in cursive manner. Though it is non-cursive in writing but there are some irregularities which some writers commit in writing this script that poses some difficulties to read Devanagari script through a machine. Some such irregularities have been described in this paper [Kumar, 2010].
Many of the challenges in offline Devnagari handwritten character recognition research is due to the complex structural properties of the script. Mixing of cursive and noncursive character symbols makes the problem still more difficult. Most of the Indian scripts like Devnagari, Bangla, Gujrati, Gurumukhi, etc. belong to the same Brahmic family of scripts having a common origin. Consequently, many structural similarities are observed among their characters. Therefore, a character recognition scheme developed for one Brahmic script may also be applicable to other scripts of Brahmic origin. In view of this, we propose to use Curvelet features for isolated handwritten Devnagari signature recognition which has recently been used successfully for recognition of handwritten Bangla characters with an overall accuracy of 95.5% [Majumdar, 2007]. Following this, we classify the extracted features along with moment invariant analysis of Hu's moment invariants and Zernike moment invariants that gives better performance [Kumar & Singh, 2005]. Beside of moment invariants we have also considered other features such as horizontal length, maximum height, aspect ratio and number of breaks in the signature sample for recognition of a particular Devnagari signature [Ramteke, 2010].
This section describes the methodology behind the system development. It discusses the pre-processing performed, the signature database, and the NN features. Signature Recognition Systems need to preprocess the data. It includes a series of operations to get the results. The major steps are as follows :
Data Acquisition: The signatures to be processed by the system should be in the digital image format (Figure 1). We need to scan the signatures from the document for the verification purpose. Data acquisition is required to acquire the signature of the user which can be based on a variety of input tools. Data acquisition process is a process where the real time inputs of signature from the digitizing tablet and the special pen are read into the CPU for processing and to store the signature in to the database. The digitizing tablet is sending the real time inputs to the CPU for further processing and storage.
Signature Pre-processing: We have to normalize the signature, resize it to proper dimensions, remove the background noise, and thin the signature. It yields a signature template which can be used for extracting the features. Therefore minimal signature pre-processing is required (Nelson, Turin, & Hastie, 1994). Other areas of handwriting analysis require large amounts of preprocessing such as slant correction, rotation correction and size normalization to reduce variations in the handwriting. However, in handwritten signature verification (HSV), most of the subtle nuances of the writing such as size and slant are indicative of the signer's natural style, removal of which would deny HSV system of useful information. The only pre-processing performed is rotation normalization [Nelson & Kishon, October, 1991]. This procedure involves extracting the baseline points from the signature (i.e. the bottoms of all non-descended characters). Linear regression is used to best fit a straight line through the baseline points.
Feature Extraction: The features extracted from signatures or handwriting play a vital role in the success of any feature based HSV system. The Devanagari script has descended from the Brahmi script sometime around the 11th century AD. It was originally developed to write Sanskrit but was later adapted to write many other languages like Bhojpuri, Bhili, Magahi, Maithili, Marwari, Newari, Pahari, Santhali, Tharu, Marathi, Mundari, Nepali and Hindi. Hindi, is the official national language of India and also the third most popular language in the world. According to a recent survey, Hindi is being used by 551 million people in India.
The basic set of symbols of Devnagari script consists of 36 consonants (or vyanjan) and 13 vowels (or swar) as shown in Figure 1. The characters may also have half forms. A half character in most of the cases is touched by the following character, resulting in a composite character, also known as compound character. The script has a set of modifier symbols which represent the modified shapes undertaken by the vowels, when they are combined with consonants, as own in Figure 2. These symbols are placed either on top, at the bottom, on the left, to the right or a combination of these. There are infinite variations of handwriting of individuals because of perceptual variability and generative variability. This variability effects in handwriting make the machine recognition of handwritten characters difficult.
A half character in most of the cases is required to touch the following character resulting in a composite character. Some characters of Devnagari script take the next character in their shadow because of their shape. The script has a set of modifier symbols which are used only to modify a character. These symbols are placed either on top, at the bottom, on the left, to the right or a combination of these.

Figure 1. Simplified workflow for a typical Signature Recognition System
In this paper the authors have considered total six different features of signature. Out of these six features following features the most important feature under our consideration for the process of signature verification, are Hu's Moment Invariants and Zernike Moment Invariants.
(a) Hu's Moment Invariant: Hu's introduced seven moment invariants in 1962. The non-orthogonal centralized moments are translation invariant and can be normalized with respect to changes in scale. However, to enable invariance to rotation they require reformulation (Baradi & Kakere, 2010). Hu described two different methods for producing rotation invariant moments (Flusser & Suk, 2006). These moments having the desirable properties of being invariant under image scaling, translation, rotation, and shear in which can be defined by following equations (Equation 1 to 7).
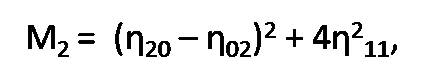
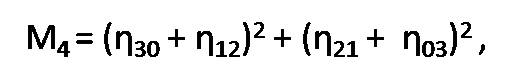
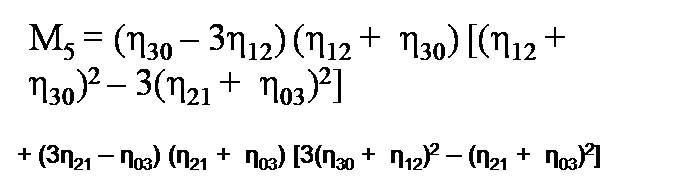
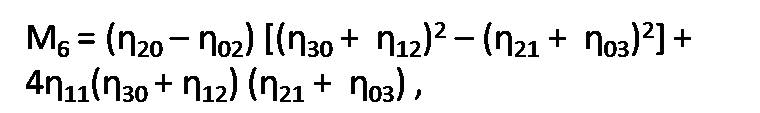
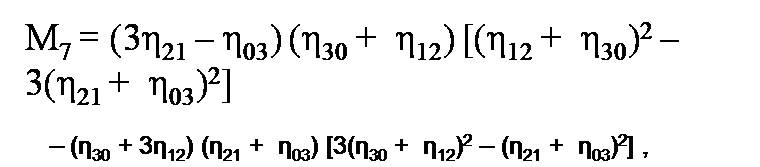
These moments are of finite order, therefore, unlike the centralized moments they do not comprise a complete set of image descriptors. The result is a set of absolute orthogonal (i.e. rotation) moment invariants, which can be used for scale, position, and rotation invariant pattern identification. These were used in a simple pattern recognition experiment to successfully identify various typed characters. This moment invariant is used for signature verification in (Chaudhari, Barhate & Bhole, June, 2009). Moments and functions of moments have been extensively employed as invariant global features of images in pattern recognition. For object recognition, regardless of orientation, size and position, feature vectors are computed with the help of nonlinear moment invariant functions.
Representations of objects using two dimensional images that are taken from different angles of view are the main features leading us to our objective.
(b) Zernike Moment Invariant: These moments first introduced by Teague (1980) based on continuous orthogonal functions called (Zernike polynomials Wang & Healey, 1998, p. 196-203). These moments are used for signature recognition [Radhika, Venkatesha & Sekhar, February, 2010, p. 12-18]. The equation (9) provides the convenient way to express the Zernike moment in terms of geometric moment in Cartesian form. The Zernike moment invariant functions are derived from (10) which is invariant against rotation and scaling factors B(x,y) refers Zernike polynomials are defined only inside a unit circle, and therefore the computation of Zernike moments requires a linear coordinate transformation from the image space to the interior of the unit circle, followed by a mapping to the pixel density of N×N image size. Zernike polynomials are a set of complex polynomials which form a complete orthogonal set over the interior of the unit circle. The form of polynomial is shown by equation (8)
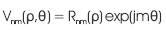
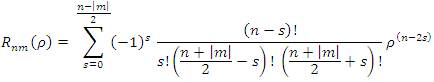
Zernike polynomials are defined only inside a unit circle, and therefore the computation of Zernike moments requires a linear coordinate transformation from the image space to the interior of the unit circle , followed by a mapping from the rectangular coordinate system to the polar coordinate system. The values of m, n can be selected to suit the desired sampling frequency. The Zernike moment of order n with repetition m for function f (x, y) is defined as:
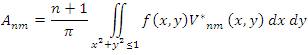
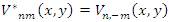
To compute the Zernike moment of a digital character image, we just need to change the integrals with summations:
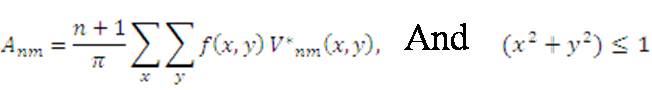
The defined features of Zernike moments themselves are only invariant to rotation. To achieve scale and translation invariance, the image needs to be normalized first by using the regular Zernike moments. The translation invariance is achieved by translating the original image f (x, y) to f(x + x, y + y), where
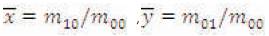
In other words, the original image's center is moved to the centroid before the Zernike moment's calculation. Scale invariance is achieved by enlarging or reducing each shape so that the image's 0th regular moment, m'00 equals to a predetermined value β. For a binary image, m'00 equals to the total number of shape pixels in the image. To calculate the Zernike moments for a given image, its pixels 2 2 are mapped to the unit circle![]() . This is done by taking the geometrical center of the image as the origin and then scaling its bounding rectangle into the unit circle. Due to the orthogonality of the Zernike basis, the part of the original image inside the unit circle can be approximated using its Zernike moments Anm up to a given order nmax using following equation,
. This is done by taking the geometrical center of the image as the origin and then scaling its bounding rectangle into the unit circle. Due to the orthogonality of the Zernike basis, the part of the original image inside the unit circle can be approximated using its Zernike moments Anm up to a given order nmax using following equation,
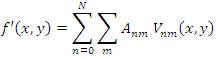
Zernike moments have simple rotational transformation properties interestingly enough the Zernike moments of a rotated image, have identical magnitudes to those of the original one, where they merely acquire a phase shift upon rotation. Thus, when considering image reconstruction from moments, the number of moments required for accurate reconstruction will be related to the frequencies present within the original image. For a given image size it would appear that there should be a finite limit to the frequencies that are present in the image and for a binary image that limiting frequency will be relatively low. As the higher order moments approach this frequency the reconstruction will become more accurate.
Few more features of a signature which are also important are as followings :
(a) Horizontal Length: This is the horizontal distance measured (Figure 2) between the two most extreme points in the x direction. It is simply the distance between the first point captured and the last point captured (Chen & Srihari, 2006). The horizontal length tends to remain stable with a practiced word and particularly with a signature, irrespective of the presence of a bounding box, horizontal line or even with no line present.

Figure 2. Horizontal length of Signature
(b) Aspect Ratio: This is the ratio of the writing length to the writing height. It remains invariant to scaling. If the user signs in a different size, the height and length will be altered proportionally to retain the aspect ratio.
(c) Number of “pen-ups”: This indicates the number of times the pen is lifted while signing after the first contact with the tablet and excluding the final pen-lift (Alexandra, 2002). This is highly stable and almost never changes in an established signature. This can be a difficult feature for a forger to discern from an off-line copy of the signature.
(d) Maximum Height: This is the distance between the lowest points in a word (the lowest descanter's depth) and the highest point in a word (the highest ascender's height) (Figure 3).

Figure 3. Maximum Height of Signature
Also removed from consideration is the final trailing stroke in a signature in examination of the trailing strokes in different signatures produced by the same signer, this stroke's height was found to be by far the most variable (Wu, Chang & Lee, 1997). The maximum height feature using the remaining captured points reflects, to some extent, the “flair” with which the author writes and the maximum distance typically traversed by the pen tip. This feature remains reasonably stable across several written samples.
Training of Database of Signatures: The extracted features are stored in to database. The human signature is dependent on var ying factors, the signature characteristics change with the psychological or mental condition of a person, physical and practical condition like tip of the pen used for signature, signatures taken at different times, aging etc. We have to consider a high degree of intra-class variation because two signatures from a same person are never same [Henniger & Franke]. Our system should consider this variation and at the same time the system should possess high degree of accuracy to detect forged signatures
We train the system using a training set of signature obtained from a person. Designing of a classifier is a separate area of research. The decision thresholds required for the classification are calculated by considering the variation of features among the training set. Separate set of thresholds (user Specific) is calculated for each person enrolled, some system also use common threshold form all users.
Devnagari language has its basic set of symbols, which consists of 13 vowels ('svar'), shown in Figure 4 and 39 consonants ('vyanjan'), shown in Figure 5. Recognition of Devnagari characters is highly complex due to its rich set of conjuncts. Devnagari is written from left to right along a horizontal line. Characters are joined by a horizontal bar that creates an imaginary line by which Devnagari text is suspended, and no spaces are used between words. A single or double vertical line called 'Purn Viram' (full stop) was traditionally used to indicate the end of phrase or sentence.

Figure 4. Devnagri vowels

Figure 5. Devnagari Consonants
The language is partly phonetic in that a word written in Devnagari can only be pronounced in one way, but not all possible pronunciations can be written perfectly. A syllable ("aksar") is formed by a vowel alone or any combination of consonants with a vowel. Each vowel except correspond to a modifier symbol. In Devnagari when consonants are combined with other consonants the consonant with vertical bar may appear as a half form. Except for the character, the half forms of consonant are the left part of original consonant with vertical bar. Here is a sample set of non-compound Devnagari characters.
We have designed a multi algorithmic signature recognition system which takes into account the conventional features as discussed above as well as it combines some of the prominent feature extraction mechanisms with newly proposed cluster based global features to develop an off-line signature recognition system [Ramteke, 2010]. The performance of system depends on how accurately the system can classify between the genuine and fraud signatures. The forgeries involved in handwritten signatures have been categorized based on their characteristic features.
A total of 660 genuine signatures were collected from a population of 66 human subjects which included 25 women and 41 men's and seven of them are left handed writers. The process flow of signature recognition system is shown in figure. Our main task is to recognizing the signature with good feature recognition techniques which provide good results on the signature recognition dataset.
We have observed the values of fluctuation for seven moment invariants on different resolution from 50x50 to 500x500, shown in Table I. We can see that the fluctuation in moment values decreases as the image spatial resolution increases. The fluctuation almost comes up to 1924.3% when the resolution is only 50x50, but rapidly decreases to 1.3% when the resolution is 400x400. The fluctuation obviously decreases as the resolution increases until to the threshold.
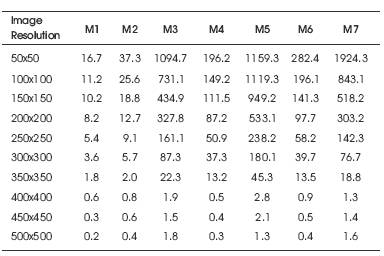
Table 1. Fluctuation of Moment Invariants on Different Resolution of Images
However, the fluctuation does not monotonically decrease any more when the resolution greater than 400x400.
On basis of these values of Table 1, we can plot the graph between variations in Hu's moment values with respect to resolution of images, shown in Figure 6. However it is not sufficient to verify the validity of a signature only by comparing the physical image of it. We have compared various features of the sample signature with the database of signatures.
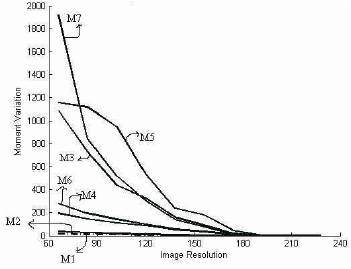
Figure 6. Fluctuation in Hu's Moment Invariant Values w.r.t. Image resolution
On basis of that comparison threshold levels are fixed by considering the signature database as the reference. And then after the threshold values obtained from the sample signature is compared with the database and results are obtained. This fact should be considered that a person's signature is not the same from time to time and it is different from one occasion to another. The overall experimental results are categorized in Table 2. With the increase of similarity false reject rate (FRR) is increased but false acceptance rate (FAR) is decreased (Herdagdelen & Alpaydm, June, 2004). The results of our examination show that in this method, the best value for the percentage of signature similarity is nearly 89.61%.

Table 2. The result of Experiments
In this point we obtain the minimum error rate (MinErrRate = min(FAR, FRR)). If we consider average error rate (AER) are as following:

The fundamental result of this study is obtaining the average of minimum errors not in the maximum surface similarity. We have the minimum value for AER when the value of the FAR and the FRR are the same, the point is called equal error rate (EER). As a matter of fact, getting the best performance, we should consider 80% ≤ SS ≤ 85%. It can be observed that when the correctness of a signature is its high similarity to the original one, the correct signatures will be rejected because of minor differences and this trend will decrease the efficiency of the system. FAR for random forgeries (FAR-random), and FAR for skilled forgeries (FARskilled). It is natural to notice that the FAR-random curve is lower than the FAR-skilled curve, since in random forgeries the signer has no previous knowledge and/or training on the signature she/he is forging. These classifiers show a total error rate below 2% and 1% respectively in the context of random forgeries.
With the higher resolution of images, the fluctuation is lower. However, the computation of moment invariants will increase when the resolution increases (Mautner, Rohlik, Matousek & Kemp, 2002). As a consequence, the research of relationship between the resolution of images and computation is necessary. The findings may be summarized as follows: (1) The moment invariants change as images scale or rotate, because images are not continuous function or polluted by noise; (2) The fluctuation decreases when the spatial resolution of images threshold; (3) The computation increases quickly as resolution increases. The proposed algorithm can be used as an effective signature verification system. The error rejection rate can further be improved by using better techniques for rotation, blurring and thinning. Using these algorithm random and simple forgeries can be easily detected. To decrease the fluctuation of moment invariants, the image spatial resolution must be higher than the threshold of scaling and rotation (Boyce & Hossack, 1983). However, the resolution cannot be too high, because the computation will remarkably increase as the resolution increases. Therefore, the choice of resolution must balance computation and resolution on the real application increases.
Future development of software is possible and in fact is very useful in order to increase its efficiency and flexibility in use. Matlab is powerful software when comes to mathematical operations but it uses a lot of vectors and matrix (Jain, Griess & Connell, 2010). These matrices and vectors uses too much memory, hard disk and slow down the processor unit of the computer hence, coding can be done in c, c++, java etc. The character recognition system that is developed is only able to recognize the single/isolated character. Further research is needed to develop a system that recognizes the connected/joined characters [Hu, 1962].
The pleasure, the achievement, the glory, the satisfaction and the construction of my research work cannot be thought of without the few, who apart from their regular schedule spared their valuable time. The author owe a debt of gratitude to Prof. Sandeep B. Patil for providing his timely advice, constructive criticism and excellent supervision.