Civil engineering is one of the oldest branches in engineering. At early days there were not many disciplines in civil engineering. With development in mathematics, civil engineering evolved into many disciplines such as finite element analysis, structural dynamics, non-linear analysis of structural elements. Without mathematics civil engineering is incomplete because every simple problem to complex problem involves numerical analysis. Therefore, it is the time to link the civil engineering with programming languages via mathematics in a soothing manner. The best programming language is MATLAB and it clones like Scilab, GNUOCTAVE for students, academicians and practicing civil engineers alike (Honson, 2011). Therefore everyone can enjoy the concepts in a better way.

We can also develop applications by using the above mentioned programming languages, thereby saving the time and also resources. At present, there are many software available to solve complex problems to trivial problems and 90% of these software are not open source.

Shear force and bending moment diagram plays an important role in design of building components like beam column, etc. Though important, most students felt it difficult to draw shear force and bending moment diagram. Therefore, recent studies (Suh, 2014) show that by developing an educational software for beam loading analysis using pen-based user interference created an interest to link the civil engineering problems with programming language, such that faculty can create interest in students to solve complex engineering problems. Using of Python programming language is popular among student as well as teaching community. Faculty can develop codes for learning beam bending which could aid the students a lot. Many authors had developed the code to draw the shear force and bending moment diagrams but have not developed generalized application for shear force and bending moment (Bhogade & Bolli, 2015; Sobaszek, 2013). This paper will fulfill this requirement by developing a generalized application to draw shear force diagram and bending moment diagram. Some authors developed MATLAB, GUI'S to analyze cantilever beams and they also developed shear force diagram and bending moment diagram (Hossain & Al-Faruk, 2017). But these are not generalized applications to get shear force diagram and bending moment diagrams (Linge & Langtangen, 2016).

The main objectives of this paper are:

• To develop a generalized code to draw shear force and bending moment diagrams by using MATLAB and GNU OCTAVE
• How to use singularity functions with programming languages?
• To develop a good aid to draw the neat SFD and BMD diagrams and thereby create an interest among students in programming languages like MATLAB and other allied programming languages (Matworks, n.d.).

The procedure for generalized SFD and BMD using singularity functions has to be found using programming languages (MATLAB, GNU OCTAVE) as shown in Figure 1. Separate functions like step, ramp, quadratic and cubic are written and includeed in main function by name sfbm.m.

Figure 1. The Functions Written in MATLAB and GNU OCTAVE

2.1 Singularity Functions

Singularity functions are discontinuous functions or their derivatives are discontinuous. Here, singularity functions are used to draw shear force and bending moment diagrams by using MATLAB and GNU OCTAVE.

The following are the singularity functions which were implemented in this paper.

• Unit step function
• Unit ramp function
• Quadratic function
• Cubic function

2.1.1 Relationships of Singularity Functions

The unit step function is used to draw shear force diagram when UDL is acting on any beam. The continuous-time unitstep function is defined as,

f(x-a) = 0 for x < a = 1 for x > a

The units step function is used to draw the shear force diagram under the point load and bending moment diagram due to moment. The ramp function is used to draw the bending moment diagram under point loads and shear force diagrams under uniformly distributed loads. The quadratic function is used to draw the bending moment diagrams under uniformly distributed loads and shear force diagrams under uniformly varying loads. The cubic function is used to draw the bending moment diagrams under uniformly varying loads. The summary of functions are given in Figure 2 and Table 1.

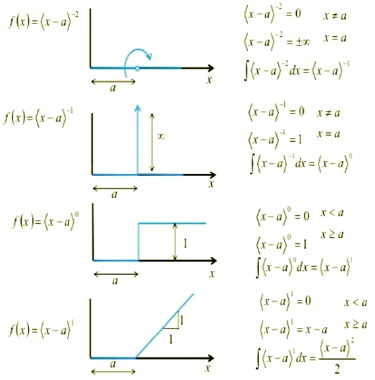
Figure 2. Summary of Singularity Functions

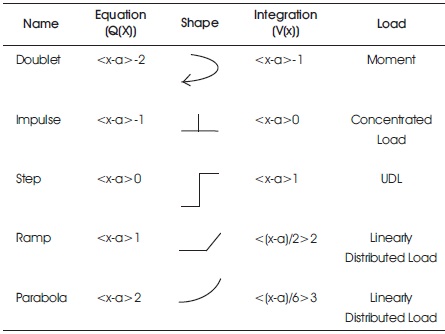
Table 1. Summary of Singularity Functions with Equation and Notations

The relationship between loading, shear force and bending moments are shown in Table 2.

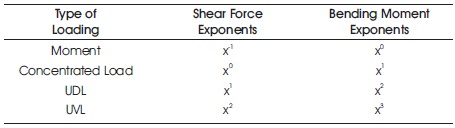
Table 2. Shear Force and Bending Moment's Exponential Variation for Different Types of Loadings

2.2 Types of Loads

• Point load
• Uniformly disturbed load
• Uniformly varying load (increasing)
• Uniformly varying load (decreasing)
• Moment

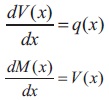
In this paper, we have denoted types of loads for 6 columns as shown in Table 3.

Table 3. Types of Orientations of Loads and Specifications Used in Coding

In loading conditions, we have taken downward direction as negative and vice versa, and clock wise direction as positive and vice versa.

The main function written in MATLAB is as shown in Figure 3. Even though GNU Octave is clone to MATLAB, some functions are different.

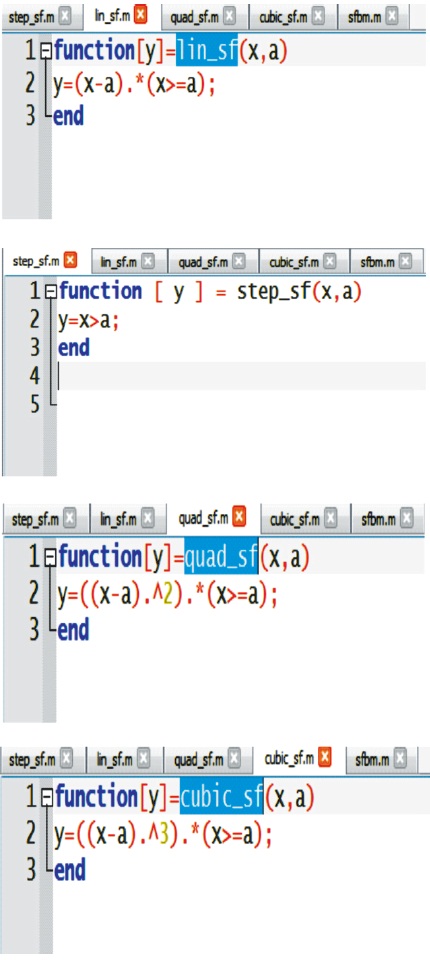
Figure 3. Singularity Function Written in MATLAB and GNU Octave

We have presented sample code to find generalized shear force and bending moment diagram for beams using singularity functions and the code is shown in Appendix.

Appendix

Code:

function [x,v,bm]=sfbm(lm,xl,xu,n)

% function sfbd calculates SFD AND BMD DIAGRAMS FOR GIVEN LOAD matrix lm

% xl =left x coordinates

% xu=right x coordinates

%lm=readxls('sfbmdata.xls')

xl=input('enter the intial distance of beam generally xl=0=')

xu=input('enter the final distance of beam =')

n=1001

x=linspace(xl,xu,n)

mrc=size(lm)

nl=mrc(1);

cnlt=mrc(2) % column number of load type last column number of lm % space allocatable

v=zeros(size(n),size(n));

bm=zeros(size(n),size(n));

for i=1:nl

ww=lm(i,4);% load intensity

xi=lm(i,1); % initial x coordinate of the load

xe=lm(i,2);% ending x coordinate of the load

if lm(i,cnlt)==0

bm=bm+lm(i,5)*step_sf(x,xi);

else if (lm(i,cnlt)==1)

v=v+ww*step_sf(x,xi);

bm=bm+ww*lin_sf(x,xi);

else if (lm(i,cnlt)==2)

v=v+ww*lin_sf(x,xi)-ww*lin_sf(x,xe);

bm=bm+ww*0.5*quad_sf(x,xi)-ww*0.5*quad_sf(x,xe);

else if (lm(i,cnlt)==3)

v=v+ww*0.5*quad_sf(x,xi)-(xe-xi)*ww*(x,xe)-ww*0.5*qua d_sf(x,xe);

bm=bm+(ww/6)*cubic_sf(x,xi)-(xe-xi)*ww*0.5*qua d_sf(x,xe)-(ww/6)*cubic_sf(x,xe);

else if (lm(i,cnlt)==4)

v=v+ww*(xe-xi)*lin_sf(x,xi)-ww*0.5*quad_sf(x,xi)+ww* 0.5*quad_sf(x,xe);

bm=bm+ww*0.5*(xe-xi)*quad_sf(x,xi)-(ww/6)+cubic_s f(x,xi)+(ww/6)*cubic_sf(x,xe);

end

end

end

end

end

end

subplot(2,1,1)

plot(x,v,'linewidth',1.5)

xlabel('distance')

YLABEL ('shear force(KN) ');grid on

subplot(2,1,2)

plot(x,bm,'linewidth',1.5);grid on

xlabel('distance')

ylabel('bending moment(KN.m')

end

In the code we have taken point load as 1, uniformly distributed load as 2, uniformly varying load (increasing) as 3, Uniformly Varying Load (decreasing) as 4, moment as 0 to find generalized shear force and bending moment diagrams.

Sample loading diagrams of the beams with different conditions are as shown in Figures 4.

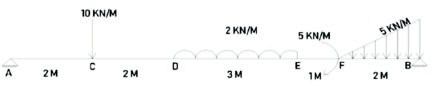
Figure 4. Diagram of Simply Supported Beam with Different Loading Conditions

After executing the codes in respective programming languages shear force and bending moment diagrams are generated as shown in Figure 5 and 6.

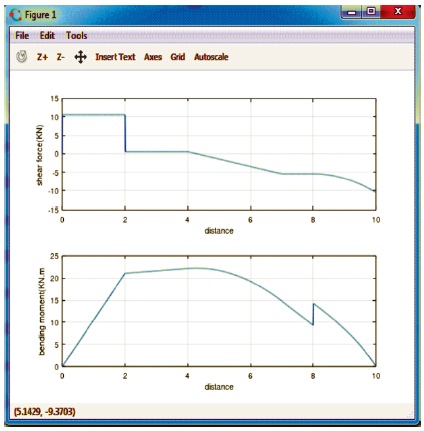
Figure 5. SFD and BMD Diagrams in GNU OCTAVE

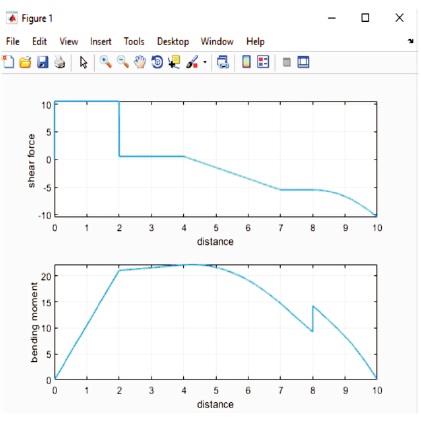
Figure 6. SFD and BMD Diagrams in MATLAB

From the outputs shown in Figure 5 and Figure 6, it is clear that by applying mathematics in civil engineering discipline via programming languages, any complex shear force and bending moment diagrams can be drawn within seconds. The programming languages will fill the gap between mathematics and civil engineering in an interesting way. This will aid both students as well as tutors to solve all types of civil engineering problems in an easy way.

From the results, it is concluded that MATLAB and GNU OCTAVE are user friendly to students and faculty to develop complex shear force and bending moment diagrams with singularity functions. From the results it is also clear that graphical results obtained is understable. Therefore, it is time to invoke interest in students by demonstrating different types of structural related complex problems with aid of mathematics and programming languages.