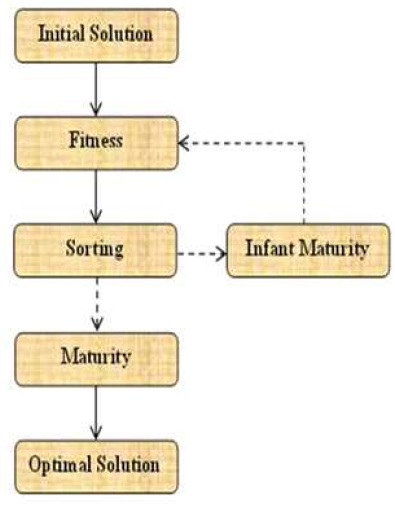
Figure 1. Overall Protocol of Evolution of Cub to Predator Technique
Most of the optimization techniques come under evolutionary and swarm intelligence techniques inspired by the behavior of different species around the world. These techniques play a vital role in solving a wide range of nondeterministic complex optimization problems and intellectually solving various real-world problems. This research paper includes a novel approach inspired by the successive hunting ability of lion from cub to predator is called Evolution of Cub to Predator (ECP). ECP algorithm based on evolving hunting ability of cub learned from parent-lion, environment, and siblings. In the proposed algorithm, lion-cub learns their hunting ability in two ways; initially from parents and resident mate cubs called infant-maturity. Later on, the cub gets matured by develop their hunting ability through real-world executions. The interpretations of cub's intellectual, social behaviour towards its environment place them on top position in the survival of the fittest later on. The investigation includes ten different benchmark test functions for evaluating the performance of the ECP. The result exhibits the proficient execution of ECP for searching the global optimum with several benchmark functions.
The most vital among an assortment of points that identify with computation are algorithm validation, complexity estimation and optimization (Desale et al., 2015). Natural computing is a novel way to solve real life problems inspired by life (de-Souza & Costa, 2009). To solve the issue of extensive search space, one of the best recommendations is to utilize meta-heuristic algorithms. The meta-heuristics are partitioned into two classes as indicated by our knowledge, biological, and bio-inspired algorithms (Kahvazadeh & Abadeh, 2015). Many metaheuristic optimization strategies have been created to solve such troublesome optimization problems (Said et al., 2014). In past decades, most of the heuristic algorithms have been established to resolve combinatorial and numeric optimization problems (Sakulin & Puangdownreong, 2012). However, a new heuristic and most effective algorithms are expected to solve difficult and complicated real-world optimization problems (Oftadeh & Mahjoob 2009). One of these is the Lion Algorithm (LA), which is effectively connected with engineering optimization problems. The proposed Lion algorithm emulates the social behavior of animals when catching a prey in the way wolves hunt (Bouzaida et al., 2013).
Lions are exceptionally compelling a direct result of their solid sexual dimorphism in both social behavior and appearance. The lion is a wild felid with two sorts of social association; residents and nomads. Residents live in gatherings called pride (Yazdani & Jolai, 2016). Pride is the term used to allude lion's social framework, in which resident females are attending males and give birth to offspring, sharing an area called as region to tranquil connections. A cub needs 2-4 years to accomplish sexual development, so that the regional lion needs to shield the domain for a similar number of years. In the middle of these 2-4 years, nomadic lions may attempt to attack the pride, which we call as regional defense (Rajakumar, 2012). If another partner of males could take control over a pride, they would try to kill young cubs who were sired by their forerunners. Accordingly, the individuals from a pride, particularly male lions, are not relentless. Frequent male takeovers may be a clarification for why the male lion can be extremely solid and be the"king of beasts" (Wang et al., 2012). In our algorithm, each hunters indicates one solution to a specific issue. Like real animals which hunt in group, artificial hunters coordinate to discover and get the prey; i.e., the optimum point in our work (Oftadeh et al., 2010).
A significant anticipation of this research is to derive a novel bio-inspired optimization technique. This technique inspired from upgrading lion's hunting ability to resolve testing benchmark problems. Successful execution intends to implement in real-world problems.
Zhang et al. (2019) proposed a technique based on Cuckoo Search (CS) and Differential Evolution (DE), a hybrid optimization algorithm, called CSDE, to solve the constrained engineering problems. Furthermore, these two techniques proved to be especially appropriate for engineering problems.
Omran and Al-Sharhan (2019) have proposed the Ant Colony Optimization (ACO) algorithm which is an optimization technique that can be used effectively to resolve many difficult discrete optimization problems. In addition, the results of the comparative analysis show the superiority of ACO compared to other tested algorithms.
Lou and Yuen (2019) proposed benchmark testing offers a performance measurement for an evolutionary algorithm before placing it into applications. Experimental results unveils that each technique accomplishes the best robustly on its unique favorable problem.
Humphreys and Ruxton (2018) have proposed more than atos is known as death-feigning and, they maintain further suitably, Tonic Immobility (TI) is an under-reported, but fascinating anti-predator strategy adopted by various prey late in the predation order, and often follows physical interaction by the predator. This research deliberates the potential evolutionary inspiration of certain predator types in the development of the strategy in prey, and other nondefensive circumstances that have been suggested to address TI.
Li et al. (2017) proposed the Artificial Fish Swarm Algorithm (AFSA) as a proposed promising swarm intelligence optimization algorithm, yet there are still some limitations, such as low optimization precision and convergence rate.
Cuevas at el. (2013) proposed swarm intelligence which is a research field that models collective behavior in swarms of insects or animals. In that study, a novel swarm algorithm named Social Spider Optimization (SSO), which was proposed for solving optimization tasks.
The comparison examines several standard benchmark functions that are commonly considered within the literature of evolutionary algorithms. The literature mentioned above guides us to understand the working procedure of employed techniques. This understanding paves the research for deriving a novel optimization technique, which resolves the limitation of conventional methods. The driving factor behind each technique is an updating process, which plays a vital role to solve particular problems. This review includes both evolutionary and swarm intelligence techniques, which urge incorporating both strategies on intend novel technique
With a profound understanding of lion and its environment, we can inspire many search-based optimization techniques at regular interval from recent literature. In this paper, a detail interpretation of lion cub's evolving their hunting ability from childhood to adult, which inspired to derive Evolution of Cub to Predator (ECP) ECP, a search based optimization technique as a flow chart illustrated in Figure 1. The couple of features inspired from lion's cub are, learn from alpha cub during play time and learn from adult lion during real hunting. These inspired them to derive a updating process like infant maturity and maturity. Infant maturity utilizes an evolutionary strategy for updating process and maturity process utilizes swarm intelligence approach for updating process. Here, preliminary updating process is infant maturity, because the evolutionary approach swarm intelligence approach has evident better performance in various platform. Subsequently, the maturity updating process is applied to improve the performance even better. This research utilizes the 10-benchmark testing function for evaluating the performance of the proposed ECP and other comparative techniques are Evolutionary Algorithm (EA), Genetic Algorithm (GA), Differential Evolution (DE), Ant Colony Optimization (ACO), Particle Swarm Optimization (PSO), Cuckoo Search (CS), Social Spider Optimization (SSO), Artificial Bee Colony (ABC), and Artificial Fish Swarm Optimization (AFSO).

Figure 1. Overall Protocol of Evolution of Cub to Predator Technique
Like the other search base optimization technique, ECP begins with generating a random initial solution with the length of ten, searching space belongs to the boundary [-1 1], and several populations can be varied from [10 to 50] for analytical purpose. Here, individual solution refers cub and solution length refers capability of each cub, which represents as C1, C2, upto C5. An Example for generating initial random solution is shown in Figure 2.
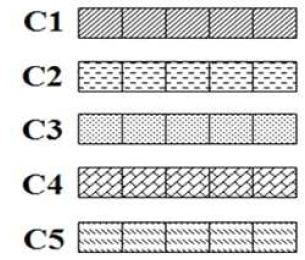
Figure 2. Solution Generation (Cubs)
This process utilized to evaluate initially generated random solution and to evaluate how close the generated solution to the optimal point. Here, we use De- Jong's Type I function and nine other test functions for f i tness computation process to evaluate the performance of the initial solution. The example test- function is,
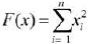
The Equation 1 mentioned above is the test function used to evaluate the performance of employed techniques along with proposed ECP technique. On other words, the ability of every cub to be tested to evaluate their position in the pride.
With an exposure of the above process, the position of cubs in the pride is arranged based on its capability (Fitnessstrong) in that age group. Then, the collections of sorted cubs are otherwise called as resident Rbest and top in that list best is αbest.
This process is considered as an updating process, and this process updates initially generated random solution based on evolutionary modus operandi. Initially, cubs try to learn how to play from a fellow mate; this procedure influences us to find the updating process. The best solution for pride at that age group αbest will control the remaining pride members, which is illustrated in Figures 3 to 5. This process is similar to crossover and mutation in the evolutionary technique. The crossover and mutation rate taken for this process is 0.2, which is common throughout this entire process. Subsequently, fitness computation has taken part in the previously defined function (Equation 1) to evaluate the updated solutions.
After sorting, αbest attain after infant maturity compare with initially generated αbest if it is minimum then the values are replaced in αbest else previous αbest values stick on.
This is a kind of updating process that comes after the preliminary updating process, whereas the cubs behave intellectually well in hunting by their own interpretation. The following Equations 2 and 3 utilized for further updating.
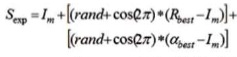
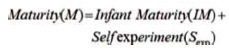
Whereas, Sexp represents self-experiment, rand indicate random value between zero and one, cos (2π) is a learning factor based on its environment, R indicate resident best, αbest indicate cub at that age group (iteration).
This process is repeated until optimal solution is attained, from the second iteration the infant maturity and maturity process name is replaced by rational behaving, but the process remains the same.
Figure 3. Influence of a to Other Resident Mate

Figure 4. Updating a Itself
Figure 5. Infant Maturity (I )
This entire process implemented in the working platform MATLAB 2016a supported by i3 processor having 6 GB RAM @ system speed of 2.20 GHz. This investigation includes ten different benchmark test functions (exhibit in Table1) to evaluate the performance of ECP. The performance evident the superiority of ECP over contest techniques in all ten test functions. The contest techniques are EA, GA, DE, ACO, PSO, CS, SSO, ABC, and AFSO.
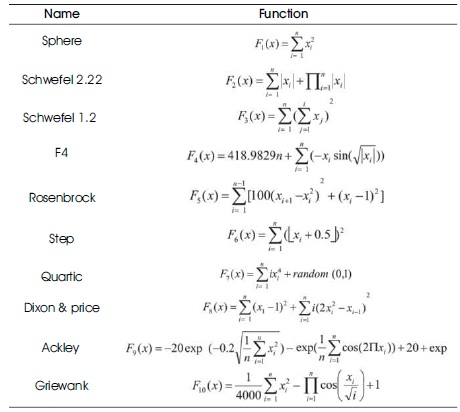
Table 1. Test Function Utilized for Investigation
Figures 6 to 15, it is noted that swarm intelligence techniques perform better than evolutionary strategy. ECP exhibits the least error value; in sphere the difference between target and attained value is 1.05e-05, in Schwefel 2.22 it is 0.009, in Schwefel1.2 it is 3.2e-07, in F4 it is 1.10e- 07, in Rosen brock it is 7.10e-07, in step it is 3.20e-08, in quartic it is 0.001, in Dixon & Price it is 0.0017, in Ackley it is 1.20e-06, in Griewank it is 1.02e-08. In general, ECP achieves least average error value of 0.001171288, which is superior compared to other techniques. Figures 6 to 25 illustrates converging performance of employed strategy and swarm intelligence technique strategy for further enhancement.
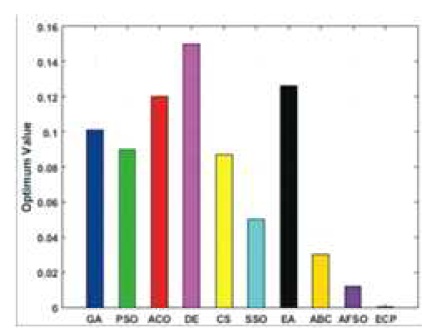
Figure 6. Performance of Employed Techniques for Finction - Sphere
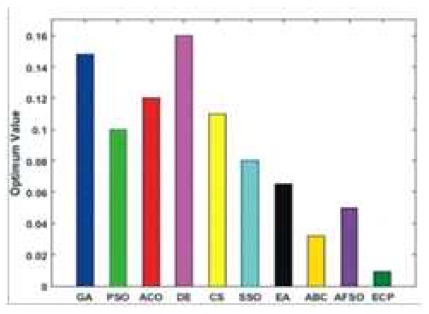
Figure 7. Performance of Employed Techniques for Finction - Schwefel 2.22
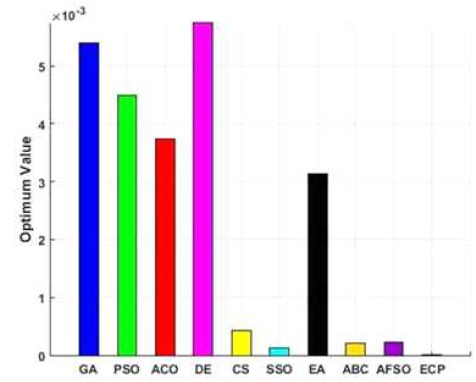
Figure 8. Performance of Employed Techniques for Finction - Schwefel 1.2
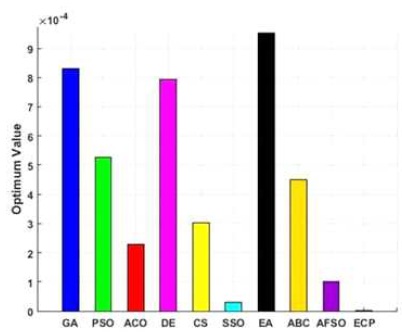
Figure 9. Performance of Employed Techniques for Finction - F4
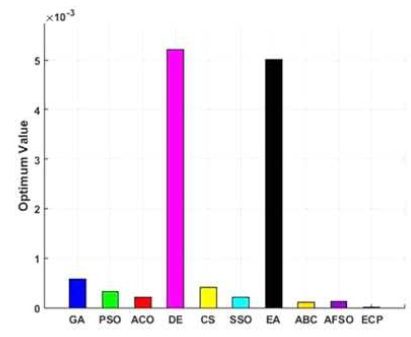
Figure 10. Performance of Employed Techniques for Finction - Rosenbrock
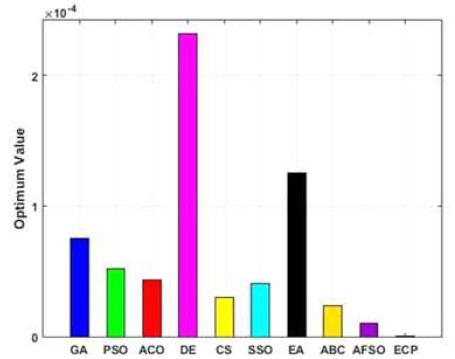
Figure 11. Performance of Employed Techniques for Finction –Step
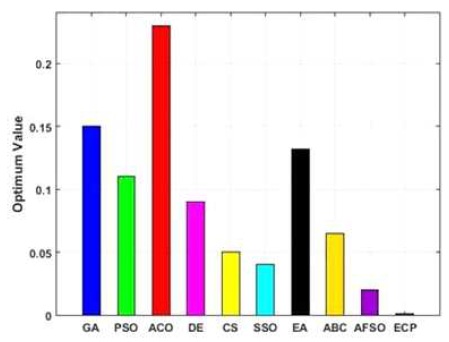
Figure 12. Performance of Employed Techniques for Finction - Quartic
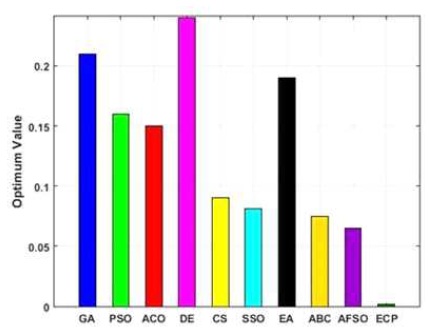
Figure 13. Performance of Employed Techniques for Finction - Dixon & Price
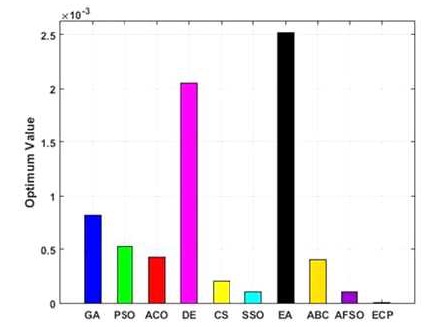
Figure 14. Performance of Employed Techniques for Finction - Ackley
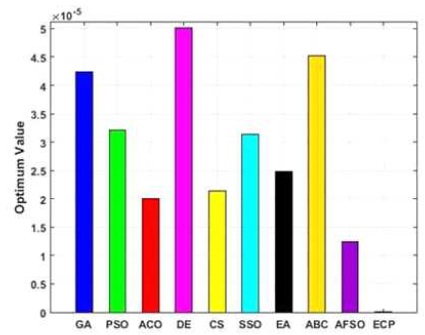
Figure15. Performance of Employed Techniques for Finction –Griewank
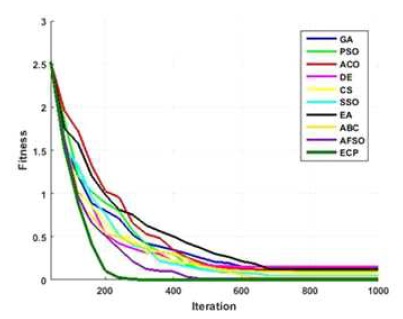
Figure 16. Converging Performance of Employed Techniques for Finction - Sphere
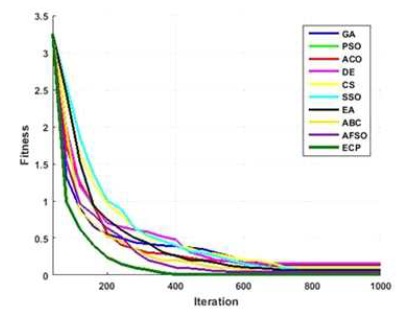
Figure 17. Converging Performance of Employed Techniques for Finction - Schwefel 2.22
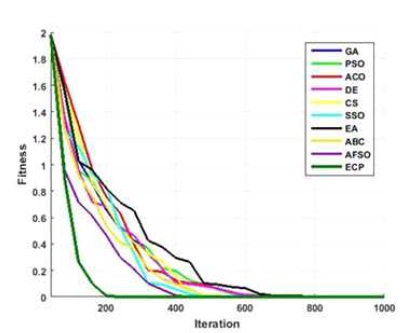
Figure 18. Converging Performance of Employed Techniques for Finction - Schwefel 1.2
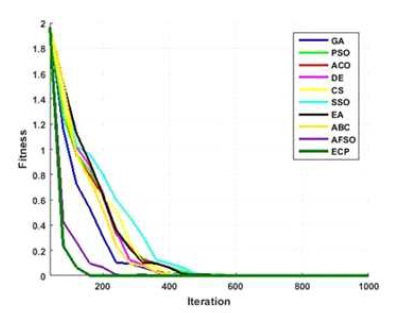
Figure 19. Converging Performance of Employed Techniques for Finction - F4
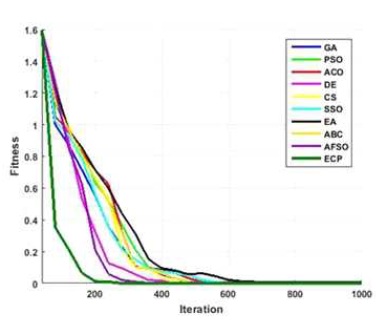
Figure 20. Converging Performance of Employed Techniques for Finction –Rosenbrock
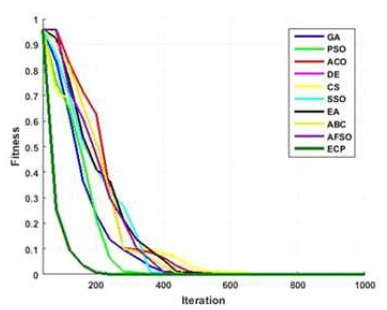
Figure 21. Converging Performance of Employed Techniques for Finction –Step
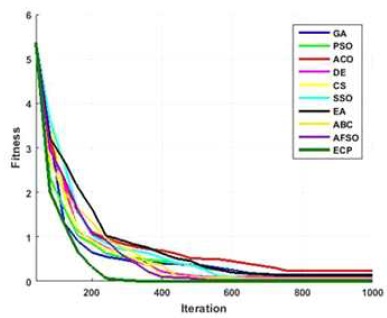
Figure 22. Converging Performance of Employed Techniques for Finction - Quartic
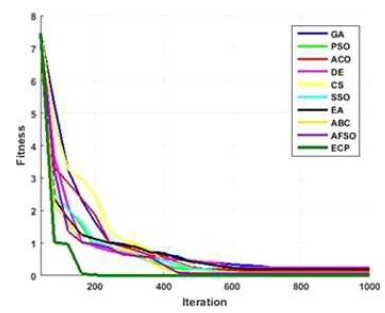
Figure 23. Converging Performance of Employed Techniques for Finction - Dixon & Price
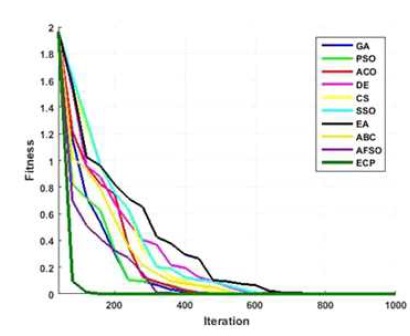
Figure 24. Converging Performance of Employed Techniques for Finction - Ackley
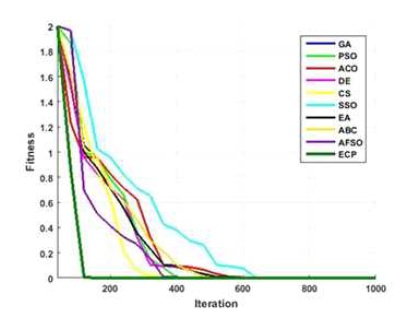
Figure 25. Converging Performance of Employed Techniques for Finction –Griewank
Table 2 exhibits the average test function error values that can be attained from each of the techniques employed. The performance unveils the superiority of proposed ECP over other employed techniques in the context of solving benchmark problems. AFSO has unveiled the second best performance in the contest and the third position goes to ABC. The reason behind the successful execution is a hybrid of evolutionary and swarm intelligence techniques, which elevates the performance of ECP.
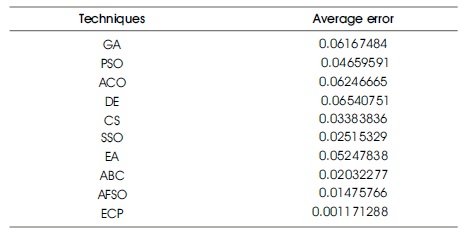
Table 2. Technique-Wise Average Test Functions Error Value
The purpose of this research is to accomplish a novel ECP for solving optimization tasks. As discussed, this technique includes a couple of updating processes like infant maturity and maturity. This elevates the performance of ECP over contest techniques. ECP has been investigated and tested with ten benchmark functions. The performance of the proposed method is compared with DE, GA, EA, PSO, ACO, SSO, ABS, AFSO, and CS. It is evident from the investigation that the proposed method performed stable and reliable operation in the entire testing benchmark functions. The ECP's significant performance are there updating the strategy allows for a better cub in the search space and increases the probability of finding a global optimum solution. In general, ECP achieves a least error of 0.001171288 (i.e., the difference between the target value and obtained value), which is proficient than other employed techniques. In the future, this technique is anticipated to be implemented in real-world problems for testing in performance capability, and limitations in the results can be utilized as a feedback to enhance the performance.