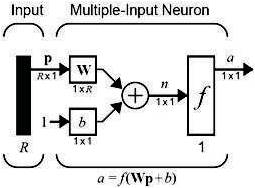
Figure 1. Signal Neural Network
In this paper, we introduce a new learning algorithm for neural network. A New Adaptive bacteria foraging optimization based on particle swarm optimization(ABFO_PSO) is used in learning neural network. This paper reviews Feed Forward Neural Network (FFANN), and the drawback of back- propagation learning method. Particle Swarm Optimization (PSO) is also described. Moreover, using the PSO in learning neural network is reviewed. Bacterial Foraging Optimization (BFO) is a novel heuristic algorithm inspired from forging behavior of E. coli. It is predominately used to find solutions for real-world problems, but it has problem with time and convergence behaviour. To introduce ABFO_PSO, that provide solution for BFO problem, we make a hybrid between PSO and BFO. Moreover, BFO and ABFO_PSO are applied for learning neural network. The comparison between the results of ABFO_PSO, BFO and PSO for learning neural network shows the strength of new method.
Feed-Forward Artificial Neural Network (FFANN) is a common type of neural network used in a wide range of classification problems. Commonly this kind of neural network needs to be trained in order to perform a good classification rate. This training phase usually means the use of the back propagation algorithm. The Back-Propagation network not only has strong mathematical theory, but also can approximate any arbitrary function. However this algorithm has shown some disadvantages related with the computational resources used in some applications. One of the problems is that all of gradient algorithms merely have local search ability. Training procedure for FFANN is a procedure of optimizing weights of neural network. Therefore, we can use global optimization method to overcome disadvantages of BP algorithm. Training neural network using PSO is proposed in many researches (MAN Chun-tao, WANG Kun& ZHANG Li-yong, 2009), (Andrich & Andries, 2010), ( Jun Liu and Xiaohong Qiu, 2009), ( MarcioCarvalho & Teresa, 2006), ( Yong Gui He & Li Bo., 2009). In this paper, BFO is used.
Bacterial Foraging Optimization (BFO) was first proposed by Passino in 2002. It uses the natural foraging strategies of E. coli bacterium cells that take necessary action to maximize the energy utilized per unit time spent for foraging. Recently BFO has attracted much attention from the computational intelligence community and has been applied successfully to a number of engineering problems, such as optimal power flow scheduling harmonic estimation, PID controller design load forecasting, stock market prediction and face recognition etc. However, BFO has the problem of low convergence speed and it usually results in sustained oscillation, especially on flat fitness landscapes, when a bacterium cell is close to the optima. To improve BFO search performance, some variants of BFO was proposed which includes parameters modification ( Ben Niu, Hong Wang, Lijing Tan,& Li Li, 2011),( Xin Xu, Yan-heng Liu, Ai-min Wang, Gang Wang, & Hui-ling Chen, 2012) ( Hanning Chen, Yunlong Zhu & Kunyuan Hu. , 2008) and hybrid algorithms ( Bakwad, Pattnaik, Sohi, Devi, Panigrahi, Sanjoy Das & Lohokare, 2009), ( Kim, Abraham, & Cho, 2007).
In this paper, a new Adaptive BFO based on PSO (ABFO_PSO) for learning neural network is proposed. The comparison between ABFO_PSO, BFO and PSO in learning neural network shows the advantages of this new technique.
ABFO_PSO, PSO and BFO were implemented for the training phase of FFANN. Our benchmark tests were training process from the cancer datasets, which were taken from UCI Machine Learning Repository.
This paper is organized as follows: Section 1, states related work. Section 2, is about the neural network algorithm. Section 3, shows generic PSO. Section 4, describes BFO. In section 5, the researchers propose ABFO_PSO algorithm. Section 6, shows how to use ABFO_PSO, PSO and BFO on BFO in learning neural network. Section 7, describes the experiment. In section 8, the experiment results are shown. Final Section includes the conclusions and discussions for future research.
To improve neural network learning using optimization algorithms and to improve BFO performance many approaches are proposed.
Comparison of PSO and Differential Evolution (DE) for training neural networks( EspinalAndr´ es, Sotelo-Figueroa Marco, Soria-Alcaraz Jorge, Ornelas Manuel, PugaHectorand & CarpioMart´ın, 2011) shows that PSO works in a better way than DE in the minimization of quadratic error function as fitness function.
A novel PSO based back-propagation learning algorithm (PSO-BP), which combines PSO learning with BP learning, is proposed (Li Ting & Wu Min,2008). Test results show that the proposed algorithm has faster convergence speed and better forecast accuracy than BP algorithm and GA-BP algorithm. Besides, due to parallel characteristics of the proposed algorithm, PSO-BP can be widely used in complex system modeling.
A non-linearly decreasing modulation model to optimize the Chemotaxis step size is proposed to improve the original BFO, including adaptive modulation Index, coefficient and adaptive Chemotaxis step size range(Ben Niu, Hong Wang, Lijing Tan ,& Li Li, 2011).
The fusion of Hybrid Bacterial Foraging with parameter free Particle Swarm Optimization (HBF-pfPSO) is introduced in (Bakwad, Pattnaik,. Sohi, Devi, Panigrahi, Sanjoy Das,&Lohokare,2009).HBF-pfPSO is capable to produce good quality of optima with faster convergence.
Adaptive Bacterial Foraging Optimizer based on Field is proposed in(Xin Xu, Yan-heng Liu, Ai-min Wang, Gang Wang, & Hui-ling Chen,2012). This paper has proposed a novel adaptive scheme which is based on the field, function period and predefined maximum and minimum values, to adapt the chemotactic step size in BFO with the aim of improving its convergence behavior. The ABFOF can avoid the oscillation around the optima or the stagnation near optima for a bacterium cell.
Neural Networks are algorithms for optimization and learning based loosely on concepts inspired by research into the Nature of the brain. They generally consist of five components as shown in Figure (1):

Figure 1. Signal Neural Network
Multilayer Feed-Forward Artificial Neural Network (MLFFANN) have three kinds of layers as shown in Figure 2: input layer, hidden layer and output layer. Each perceptron of MLPs has multiple nonlinear processing elements and any element at a given layer feeds all elements at the next layer. Their main advantage is that they can approximate any input/output map and they are widely used for classification.
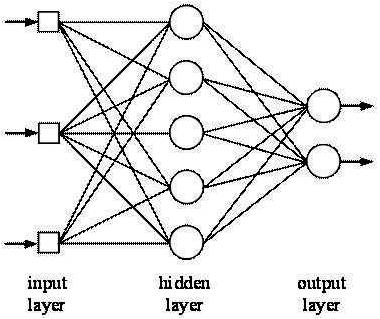
Figure 2. Multilayer Neural Network
MLFEAN neural networks, trained with a back propagation learning algorithm, are the most popular neural networks. But it has following key disadvantages:(1)because weight modification is based on gradient information, it can get caught into local optimum; (2)as the problem complexity increases due to increased dimensionality and /or Greater.
We need to choose the best optimization technique to determine the best value of the weights and biases which classify the class correctly.
Particle swarm optimization is a swarm intelligence technique which was proposed by Kennedy and Eberhartin1995 as in(Kennedy, 1995). The PSO is developed based on the following model as in (Singiresu, 2009):
Thus the model simulates a random search in the design space for the maximum value of the objective function. As such, gradually over much iteration, the birds go to the target (or maximum of the objective function).
The PSO procedure can be implemented through the following steps:
(a) The historical best value of Xj(i) (coordinates of jth particle in the current iteration i), Pbest,j with the highest value of the objective function, f[Xj(i)] encountered by particle j in all the previous iterations.
The historical best value of Xj(i) (coordinates of all particles up to that iteration), Gbest, with the highest value of the objective function, f[Xj(i)] encountered in all the previous iterations by any of the N particles.
(b) Find the velocity of particle j in the ith iteration as follows:
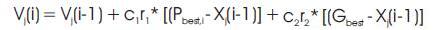
(c) Find the position or coordinate of the jth particle in ith iteration as,
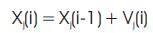
Like other swarm intelligence algorithms, BFOA is based on social and cooperative behaviors found in nature. In fact, the way Bacteria look for regions of high levels of nutrients can be seen as an optimization process. The bacteria foraging strategy can be explained by four processes as in (Singiresu,2009):
This process simulates the movement of an E.coli cell through swimming and tumbling via flagella. Biologically an E.coli bacterium can move in two different ways. It can swim for a period of time in the same direction or it may tumble, and alternate between these two modes of operation for the entire lifetime. Suppose θi(j,k,l) represents i-th bacterium at j-th chemotactic, k-th reproductive and l-th elimination-dispersal step. C (i) is the size of the step taken in the random direction specified by the tumble (run length unit). Then in computational chemotaxis the movement of the bacterium may be represented by,
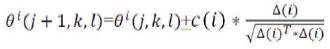
where Δ indicates a vector in the random direction whose elements lie in [-1, 1].
For the bacteria to reach at the richest food location, it is desired that the optimum bacterium till a point of time in the search period should try to attract other bacteria so that together they converge at the desired location more rapidly. To achieve this, a penalty function based upon the relative distances of each bacterium from the fittest bacterium till that search duration, is added to the original cost function. Finally, when all the bacteria have merged into the solution point, this penalty function becomes zero. The cell-to-cell signaling in E. coli swarm may be represented by the following function.
The least healthy bacteria eventually die while each of the healthier bacteria asexually split into two bacteria, which are then placed in the same location. This keeps the swarm size constant.
Gradual or sudden changes in the local environment where a bacterium population lives may occur due to various reasons e.g. a significant local rise of temperature may kill a group of bacteria that are currently in a region with a high concentration of nutrient gradients. Events can take place in such a fashion that all the bacteria in a region are killed or a group is dispersed into a new location.
The Bacterial Foraging Optimization summarized below:
Sp : Total number of bacteria in the population
NcNr : The number of chemotaxtis step
NedPi : The number of reproduction step
C(i): The length of swim
: The number of elimination-dispersal events.
: Elimination-dispersal probability.
: The size of the step taken in the random direction specified by the tumble.
For j =1, 2 … Nre
For k =1, 2 …Nc
For l =1, 2 … Sp
Perform chemotaxis step:
End for
End for
The S bacteria with the highest Jhealth values die and the remaining S bacteria with the best values split.
End for
Perform the reproduction step by eliminating _disperal step for all bacteria θi(j,k,l) with probability
0 < P
End for
ABF-PSO algorithm combines both BFO and PSO. The aim is to make PSO able to exchange social information and BFO able in finding new solution by tumble, swim, reproduction, elimination and dispersal.
In the original bacterial foraging algorithm the Chemotaxis step length Cis a constant. By this way, it is hard to keep a right balance between global search and local search. Therefore, the Chemotaxis step length is one of the most important adjustable parameters in BFO. The proper selection of the Chemotaxis step length is critical to the success of BFO algorithm.
In ABFO_PSO algorithm, PSO is used to update the length of Chemotaxis step. The velocity of bacteria still has random direction because of tumble behaviour of BFO, but the magnitude of the velocity is calculated by using social behaviour of PSO. C (i) is calculated as the magnitude of the velocity of particle in PSO:

where θbest is update every swim step θbest is update every reproduction step.
Because this combination using social information of PSO and the swarming step represents social behavior in BFO, the swarming step is avoided in ABFO_PSO. The swarming step take a long time in BFO so using social information of PSO instead of swarming step make BFO faster and more robust.
Using a previous optimization algorithm to optimize network weights lies in the following two points:
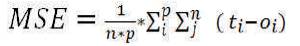
To avoid over fitting problem in classification and to generalize neural network, the valid approach is used. In this approach, data set is divided into 3 subsets:
For each set the error is calculated using equation (5).
In this section we discuss the experiment design, execution of the comparison between ABFO_PSO, BFO and PSO for learning neural network.
We chose Breast Cancer dataset instances from the UCI Machine Learning Repository (Arthur Asuncion,& David Newman, 2007):
Breast Cancer datasets include 699samples, each sample by nine features. Features are computed from a digitized image of a Fine Needle Aspirate (FNA) of a breast mass. They describe characteristics of the cell nuclei present in the image.
The samples are classified to two classes: Benign and Malignant. Those classes are not uniformly distributed. A number of Benign samples are 458 and a number of malignant samples are 241.
The researchers use MLFFNN (9-9-2) with one hidden layer, the number of neuron in hidden layer is equal to the number of data feature (inputs). Both hidden layer and output layer have sigmoid function,
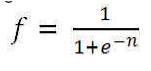
Learning algorithm in network training performance test usually has the following test:
E (error rate): the ratio between error classification samples to total number of samples.
MSE: The Mean Squared Error between target and actual output.
Each previous test is applied to all subsets of data(validationset, testingset, training set).
Because of imbalanced data set, accuracytest, recall teat and precision are used:
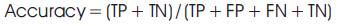
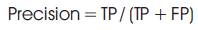
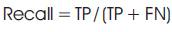
where,
TP = donors in group and model classified into group
FP = donors not in group and model classified into group
FN = donors in group and model not classified into group
TN = donors not in group and model not classified into group
Time test: The researchers make comparison between times that optimization method use in learning processes.The specifications of computer used in experiment are Intel core i5-460M processor and 4GB DDR3.
In this section we discuss the results of the comparison between ABFO_PSO, BFO and PSO for learning neural network.
Firstly, the result of mean square error and time test is shown in Table1 below:
However the Table 1 shows that PSO makes learning process inless thanone minute, it has the greatest MSE for each subset. The BFO reduce the MSE error, but it takes more than 10 minutes. Besides, ABFO_PSO has the best MSE for valid set and test set, it take less than 7 minute. The figures of curves of MSE vs iteration show the more advantages of ABFO_PSO.
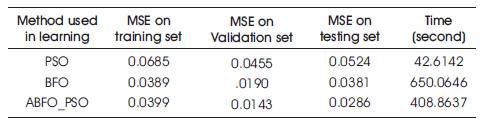
Table 1. The result of MSE and time test
As shown in Figure (3), when PSO is used, the curves of MSE train are stable, but the step length of reducing error changes randomly and the curve of MSE on validation test start to be affected after four iterations.
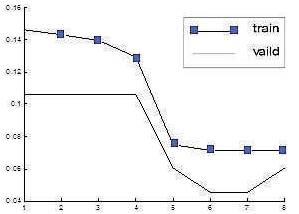
Figure 3. The result of MSE and time test with PSO
Figure (4) shows that BFO can reach to better MSE value ,but the curve of MSE on training test starts to oscillate at iteration number 8.
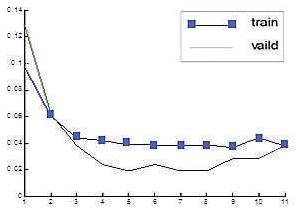
Figure 4. The result of MSE and time test with BFO
Figure (5) shows the ABFO_PSO has the best curves of MSE, which faster and more stable and reach the best minimum value. The convergence behavior of ABFO_PSO is better than BFO because it does not oscillate. The step length of reducing error begins large and decreases gradually.
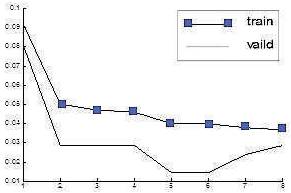
Figure 5. The result of MSE and time test with ABFO_PSO
Secondly, the result of ERROR rate is shown in Table2:
The Table 2 shows that the PSO has the largest number of error classification samples for each subset. Although BFO has the least error rate of traning set, ABFO_PSO has the least value in validation and testing set.
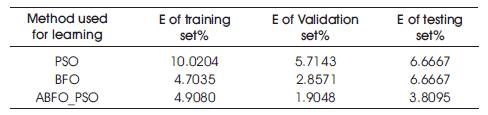
Table 2. The error rate for each method used
As Table1 and Table 2 show that ABFO_PSO has the best values of MSE and E fore validation and testing set, it makes neural network more generalizing.
Thirdly, the result of recall and precision and accuracy test of testing set is shown in Table 3, Table 4 and Table 5.

Table 3. The result of recall and precision with PSO

Table 4. The result of recall and precision with BFO

Table 5. The result of recall and precision with ABFO_PSO
PSO algorthim hase the least value of accuracy, and large difference between recall value and precision value and difference between the results of tests for two classes.
BFO algorthim can improve the accuracy, but the difference between recall value and precision value and difference between the results of tests for two classes are still clear.
ABFO_PSO has the best accuracy value and the least value of difference between recall value and precision value and difference between the results of tests for two classes. It is the best for unbalanced data set.
In this paper we provide unprecedented method, ABFO_PSO, in learning neural network. The results ofcomparison that was made between ABFO, PSO BFO and PSO in learning neural networkshow that the new ABFO_PSO ismore accurate, stable and faster. It makes neuralnetwork more generalizing and reduces the value of MSEand error rate. It can deal with unbalances data set very well. ABFO _PSO can avoid the oscillatory behavior around the optimum. The new method has the advantages of both PSO and PFO. BFO gives it the accuracy and PSO makes it faster.
For further studies,we can useABFO_PSO with other applications to show the strength of it. Trying to hybrid between ABFO_PSO and genetic algorithm is proposed to have more robust optimization theory.