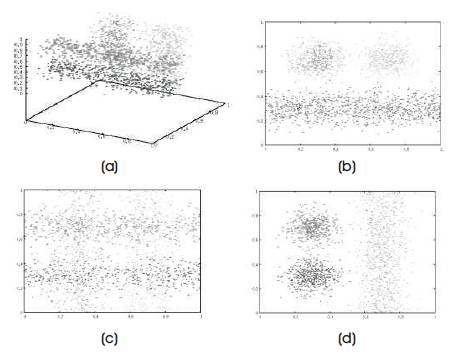
Figure 1. Existence of redundant attributes and Existence of irrelevant attributes, (a) Original Dataset, (b) Projection on the subspace {x,y}, (c) Projection on the subspace {x1 , z}, (d) Projection on the subspace {y1 , z}
In many real world problems, data are collected in high dimensional space. Detecting clusters in high dimensional spaces are a challenging task in the data mining problem. Subspace clustering is an emerging method, which instead of finding clusters in the full space, it finds clusters in different subspace of the original space. Subspace clustering has been successfully applied in various domains. Recently, the proliferation of high-dimensional data and the need for quality clustering results have moved the research era to enhanced subspace clustering, which targets on problems that cannot be handled or solved effectively through traditional subspace clustering. These enhanced clustering techniques involves in handling the complex data and improving clustering results in various domains like social networking, biology, astronomy and computer vision. The authors have reviewed on the enhanced subspace clustering paradigms and their properties. Mainly they have discussed three main problems of enhanced subspace clustering, first: overlapping clusters mined by significant subspace clusters. Second: overcome the parameter sensitivity problems of the state-of-the-art subspace clustering algorithms. Third: incorporate the constraints or domain knowledge that can make to improve the quality of clusters. They also discuss the basic subspace clustering, the relevant high-dimensional clustering approaches, and describes how they are related.
Clustering is a descriptive task in the data mining process which aims at grouping similar data sets into clusters (A.K. Jain, et al., 1988; Berkhin P, 2006). Traditional clustering techniques were designed to deliver the clusters in fulldimensional original space, by estimating the proximity between the data objects using all of the attributes of a full data set (Zhang T, et al., 1996; Han J, et al., 2011). Now-adays, as the dimensionality of data increases in advances in data collection management. But as the attributes of data increases, some of the attributes become irrelevant to some of the cluster groups. These traditional clustering algorithms are inefficient for high-dimensional data. The high dimensional data suffers several problems from the curse of dimensionality (Houle ME, et al., 2010). A two fold problem determines the summarization of the curse of dimensionality with respect to clusters. (i) The dimensionality of data grows, several dimensions may not be relevant to define cluster and may, the distance computations usually performed in full dimensional space. The cluster may form in subset of attributes, but it may not be possible to detect the clusters perfectly with the full dimensional space. (ii) The subset of dimensions related to some other cluster may be different from the subset of dimensions relate to another cluster. These two clusters may differ from the relevant subspace for a third cluster. So it may be defined as overlapping clusters in high-dimensional data, i.e. one data point belongs to cluster Cd1 in a certain subset, but the cluster Cd2 in another subset. This is not accounted in traditional clustering methods such as partitioning and density based algorithms. Figure 1 represents Existence of redundant and irrelevant attributes (Aggarwal R, et al., 1998).

Figure 1. Existence of redundant attributes and Existence of irrelevant attributes, (a) Original Dataset, (b) Projection on the subspace {x,y}, (c) Projection on the subspace {x1 , z}, (d) Projection on the subspace {y1 , z}
Aggarwal R, et al. (1998) proposed Subspace clustering to overcome the problems in state-of-art methods. Research in subspace clustering has been a challenging area for the past period. Traditional subspace clustering focuses on objects which are nearly together in their subspaces. Aggarwal CC and Reddy (2013) described although these subspace clustering techniques are efficient and effective in solving their clustering applications, their limitations are exhibited by the up-todate proliferation of complex data and the need for higher quality cluster results. The new era enhanced methods have solved proliferation problems. In this paper, the authors focus on enhanced methods to subspace clustering techniques, which is the main attention of this survey.
K. Sim, et al. (2012) scrutinized that enhanced subspace clustering can be mainly categorized in two ways, one is handling complex data and the second is improving the cluster results. Handling complex data: The fundamental subspace clustering methods only handles the 2D (two dimensional) data (object x attribute), and not the complex data of 3D data (object x attribute x time), categorical data or noisy data, streaming data. Therefore, some enhanced subspace clustering methods handle all 3D data, such as categorization, noisy, streaming data, etc. Improving the clustering results: Defined from the base class of fundamental subspace clustering approaches, which can overcome the overlapping of subspace clusters, to set tuning parameters-sensitivity problem of the basic algorithms, user may incorporate the extra information such as constraints or domain knowledge. This leads to improve quality of the clusters. In this survey, first they present subspace clustering algorithms, problems, and definitions. Second, enhanced subspace clustering algorithms and their properties, that uses improving the clustering results and their efficiency. Finally, they discuss potential problems to future research areas in enhanced subspace clustering.
In this study, they present enhanced subspace clustering methods that handle complex data and improving the clustering results, which to the best of our idea. This scenario is a challenging task. The usual surveys present a specific presentation of how the algorithms work. This survey style is different from those, as they decompose the subspace clustering problems and the results.
The domain of subspace clustering is important with massive applications for high dimensional data mining: In web text mining through document clustering (Li T, et al., 2004). There are billions of digital documents applicable today. Li T., et al. (2004) proposed an iterative subspace clustering algorithm for web text mining. In online social networks, the determination of communities in both sociologists and target marketers were done (Vidal R, et al., 2008; Vidal R. (2011), and in radio astronomy (Jang W, et al., 2007). In all of the applications considered above, fruitful knowledge is maintained in the subspaces of data.
Subspace clustering evaluate features on a subset of the data, representing a cluster.
Let DB =Op X Ap be a dataset presented in a matrix,where Op is the set of objects and Ap is the set of attributes. A Subspace cluster Cs is a sub matrix Op x Ap , where the set of objects O ⊆ Op is homogeneous in the set of dimensions A ⊆ Ap .
Three major variants are developed, via the window based, grid based and density based subspace clustering algorithms (Kriegel HP, et al., 2005). These approaches are very efficient and effective in solving their clustering problems. Lance Parsons, et al., (2004) defined the hierarchy of subspace clustering algorithms as Top down approach and Bottom up approach shown in Figure 2.
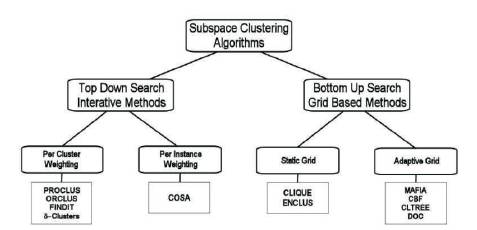
Figure 2. Hierarchy of Subspace Clustering Algorithms
In grid based clustering (Agrawal, et al. 1998), data space is partitioned into grids. Dense grids containing significant objects are used to form subspace clusters. It is done in three steps. One, find subspaces with good clustering. Second, identify the clusters in the selected subspaces. Third present the results to the users. Some efficient algorithms are CLIQUE, ENCLUS, MAFIA. Agrawal, et al. (1998) defined accuracy and efficiency of grid based methods depending on the granularity and the positioning of grids as shown in Figure 3.
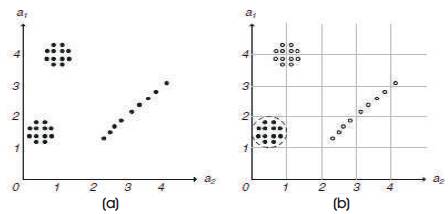
Figure 3. Accuracy and Efficiency of Grid Based Methods
A sliding window is slid over the domain of each attribute to obtain overlapping intervals. These overlapping windows of length δ are then used as one dimensional units of the grid. It overcomes the weakness of grid based methods (Liu, et al., 2009). Cluster is an efficient approach.
Kailing, et al. (2004), and Muller E, et al. (2011) defined cluster as a maximal set of density, connected points in Density based subspace clustering. In this approach, two input parameters, e and m used. An object with at least m points in its e neighborhood denotes a core object. The density, associated core objects along with border objects form a specific cluster. Density based subspace clustering algorithms can detect arbitrary shaped clusters.
Some efficient Density subspace clustering algorithms are SUBCLU, INSCY, FIRES, DUSC, DENCOS, DisH, and DENCLU. Figure 4 represents Clusters by notion (Sunita Jahirabadkar, et al. 2013).
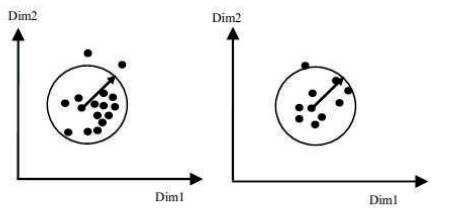
Figure 4. Clusters by Notion
K. Sim, et al (2012), proposed enhanced subspace clustering can be categorized into two important approaches, namely one, handling complex data. second, improving the cluster results. The solving problems beyond the scope of subspace clustering are maintained by enhanced subspace clustering. Important note that the desired properties of the fundamental clusters still grip for the enhanced subspace clusters and each enhanced subspace cluster has its retain properties referring that it is solved.
The fundamental clustering problem are represented on 2D datasets, and not complex data, such as a stream or noisy data, categorical.
The clustering result can be augmented in different ways from mining significant subspace clusters to using parameter-in sensitive clustering methods. They provide “true” subspace clusters.
Various Approaches and Definitions with Properties in Improving Clustering Results are given below.
Mainly two approaches are assembled in significance to subspace clustering, the one is to determine significant subspaces and then mine the subspace clusters. Determining significant subspaces can be observed as a preprocessing step and is similar to filter model of attribute selection (Dash, et al., 2002). The second is to define the significant subspace cluster and mine them.
Cheng, et al., (1999) proposed mining subspace clusters from significant subspaces to detect an exponential number of clusters being generated. Let A be the subspace in the analysis. By estimating each attribute, a ∈ A as a random variable, the entropy of A can be determined as H (a1 , . . . , a| A|). Cheng, et al. (1999) also computed the correlation of the attributes in A by the preceding equalization.
Intersest (A)= ∑ H( a ) – H (a , . . . , a| A|) a ∈A;
Properties of Entropy Subspace: K. Sim et al. (2012) :
Kailing, et al. (2003) stated a density based approach to detect interesting subspaces, and traditional subspace clusters are then mined from these subspaces.
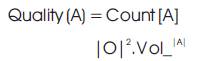
Properties of Interesting Subspace: K. Sim, et al. (2012):
The relevance model (Muller, et al. 2009) and orthogonal model (Gunnemann, et al., 2009) have been proposed to the overlapping subspace clusters. (mine high quality but minimal). These two models reduce the overlapping clusters.
In the relevance model : Let us assume the type of subspace clusters to mine and Let M{c1 ------- cn }={(O1 ,A1 ),------(On ,An } ⊆ ALL be a set of subspace clusters. Here the function cluster gain is proposed to measure the signifcance i.e.
We denote Cov (M) = Uni=1 Oi as the union of the objects in the set of clusters M. K( c) as the cost function of cluster C.
Figure 5 shows the objects in subspace {a1 a2 } and {a3 a4 } successively.

Figure 5. Set of Significant Clusters under (a) Relevance Model and (b) Orthogonal Model
{c1 ,c2 } is a set of significant clusters under the relevance model, causing the cost function dependent on the size of subspace.
It aims to detect a set of subspace clusters, that is most of the objects and attributes are involved by the clusters, but there is not much overlapping of the clusters. Each subspace cluster represents a concept (Gunnemann, et al., 2009) which is defined by the attributes of the cluster. Gunnemann, et al., (2009) first defined a concept set, which is a set of subspace clusters that have high similar set of attributes w.r.t a subspace cluster c=(O,A).
Concept Group (C, M) = {Ci ∈ M\{C}|| Ai ∩ A| ≥ β.| A|}
In Figure 3 (b) m = {c1 c2 c7 } is a set of significant subspace cluster by orthogonal Model. The set of objects of c7 is highly overlapping with those of c1 and c2 , c7 is different set as c1 and c2 .
Properties of Cluster (Relevance and Orthogonal Model): K. Sim, et al. (2012):
Subspace clusters are fully dependent of the user. For example: window based or density based subspace clusters can be used. constraints are the 'add-on' to the clusters. Object level constraints are incorporated such as must-link and cannot-link. must-link defines that a pair of objects must be in the same cluster. cannot-link defines that a pair of objects cannot be in the same cluster.
Properties (Sim, et al., 2012):
The definition of actionable is generalized from actionable patis to meaterns. The ability to suggest a profitable action for the decision-makers (Kleinberg, et al., 1998). Sim, et al., (2010) proposed actionable subspace clusters. They are useful in financial data mining. The continuous attribute known as utility to measure the actionability of the cluster utility is similar to the objectlevel constraints, but it is continuous that mainly actionable subspace clusters are mined 3D datasets. D=O x A x T.
The present subspace clustering requires the user to set parameters and the clusters that satisfy these parameters are returned. Mainly two categories are classified: cluster parameters and algorithm parameters where cluster parameters are used in cluster definitions. Algorithm parameters are used in guiding the clustering process. Consider, the parameter k in k-means clustering algorithm. On the other hand, the user selected centroid is also a cluster parameter. Some cases, both clusters and algorithm parameters can be applied. For example: constraints as must-link and cannot–link (Wagstaff, et al., 2001) are cluster parameters. They can be used in improving the quality of the cluster process. In other example, the minsize threshold as a cluster parameter and algorithm parameters. We can also categorize the parameters as semantical parameters and tuning parameters based on their usage (Kriegel, et al., 2007). It is used to tune the efficiency of the quality of the clusters or the algorithm. Semantic parameters are meaningful parameters, describing the semantics of the clusters and domain knowledge of the user can be incorporated into these parameters. Table 1, describes the parameter matrix (K. Sim, et al., 2012).
Table 2 presents the desired properties of the subspace cluster approaches have: Compared to the traditional subspace clustering approaches, the enhanced subspace clustering approaches have desired properties (K. Sim, et al., 2012).
Here we present the desired properties (K. Sim, et al., 2012) of different subspace approaches. So the reader will first follow the problems and what desired properties they explore in their clustering results. Later the reader will understand the results and their properties, and if the properties of the solutions do fulfill the desired properties that the problems seek. In future many variations of subspace clusters have been proposed to deal with various types of data and solve different problems. We will use deriving models to represent the results. All these proposed techniques have the potential to be future research areas of enhanced subspace clustering.
Nowadays, due to the advancement of data collection and increase of data is a challenging task. So the research trend has moved from traditional clustering to enhanced subspace clustering. In this review, the authors have presented the enhanced subspace clustering paradigm. As with any approach, enhanced subspace techniques finds useful and improved results depending on the selection of a particular approach and proper tuning of the algorithm with i/p parameters. This paper has discussed the concept of traditional subspace clustering and enhanced subspace clustering is desired properties of different types of approaches. Further, they will study the implementations and compare their solutions. Research in enhanced Subspace clustering is an exciting area to mine the high dimensional data sets efficiently.