Scheduling problems arise in almost all situations where tasks or jobs have to be performed under resource limitations. Most of these problems are often difficult, as they require satisfying various conflicting constraints. There are various types of scheduling problems such as production scheduling, timetable scheduling, project scheduling and employee scheduling. Usually, jobs can be scheduled anywhere along a time scale provided constraints are satisfied. It is assumed that the duration of each job is known in advance. However, if the starting time of each job is specified, it becomes a restricted version of the general scheduling problem. This version is known as the interval scheduling problem because the time interval in which each job has to be performed has been specified.

In the interval scheduling problem, the resource allocation changes over time, and it could be considered as a dynamic resource allocation problem. The earliest works on interval scheduling problem have appeared in 1950s, where a tanker scheduling problem was formulated by Dantzig, and Fulkerson (1954). The basic interval scheduling problem was solved by Ford, and Fulkerson (1962).

The paper is organized as follows. In the section 1, we present the basic interval scheduling problem. The objectives and methodology are presented in section 2. Section 3 discusses a greedy based algorithm for the basic interval scheduling problem. Section 4 deals with a lower bound for the number of machines required. We present a simple numerical example in section 5. Section 6 presents the results and discussion based on the test problems considered. Conclusion is presented in the last section.

We can state the basic interval scheduling problem as given below: let us assume that we are given a set of n intervals of the form [s_j , f_j ), where sj < f_j for j = 1, 2, .., n. Each interval represents the starting time and finishing time for a given job j. Each of these jobs require uninterrupted processing during the given interval. That means, each job has to be processed using a single machine or processor only without any interruption. At most one job has to be processed in a single machine and the machine is assumed to be always available. Without loss of generality, we can assume that s_j and f_j are non-negative integers. We assume that no overlapping of jobs are allowed. That means, no two jobs assigned to the same machine will have overlapping time intervals.

Interval scheduling problem can be considered as a resource allocation problem where a single resource is shared among different jobs so that a given objective is optimized(Ibaraki, and Katoh,1988). The methods for the basic interval scheduling problem have also been proposed by Gupta, et al. (1979), Hashimoto, and Stevens (1971), and Gertsbakh, and Stern (1978). Most of the interval scheduling problems are NP hard and no exact algorithms are available. Approximation algorithms may be formulated to solve these problems(Hochbaum, (1997), Vazirani (2002)).

There are several variants of the basic interval scheduling problem. In one variant, we need to minimize the total costs to process all given jobs on non-identical machines (Bhatia, et al., 2003). Another variant is the interval scheduling with given machines. In this variant, it is assumed that the machines are given and the objective is to maximize the number of jobs that can be feasibly scheduled(Arkin, and Silverberg, 1987).

The objective of the study is to process all jobs using a minimum number of machines. In solving this problem, we try to obtain the minimum possible number machines or processors required to perform all the given jobs. We attempt to come close to this number as far as possible.

We try to construct a fast algorithm to solve this problem. The methodology we use includes constructing a onepass algorithm, which is constructed using a greedy based approach in determining the minimum number of machines.

We shall present a greedy based algorithm to solve the basic interval scheduling problem.

In each machine t, we try to place each job as tightly as possible, but without overlapping. This is done by arranging the starting times of jobs in the ascending order. When we assign the first job on machine t, we move to the next job k according to the ascending order of starting times. Initially, k = 1. If s_k+1 < f_k , it is not possible to assign job k+1 to machine t, due to overlapping. Then, we move to the next job in the order until we encounter a situation where s_k+1 ≥ f_k. Then we assign the job k to the machine t. We continue this process until we reach a stage where after p jobs, then the last job in the list is encountered. Then, no more assigning of jobs to the same machine t is possible. The jobs that have been assigned to machine t are kept in a tabu list to prevent them considering for the subsequent assignments with other machines.

Then we start assigning jobs to the next machine. We follow the same procedure until no more jobs could be assigned to the machine. This process continues until the tabu list is full. Then, we declare that the number of machines required for assigning all jobs, as the maximum number of machines in which jobs are assigned.

Before starting assignment of jobs, the given set of intervals are arranged in the ascending order of start times. Consider the k_th job and p_th job where k < p, after rearrangement. Then, these should satisfy.

[s_k , f_k ) and [s_p , f_p ) such that s_k ≥ s_p

Algorithm

(1) Arrange the intervals (s_j , f_j ) where s_j < f_j for j = 1, 2, ..,n, in the ascending order. Place the jobs in a new list.

(2) Start assigning jobs to machines from the new list. Let the current machine is t. Initially, t = 1. Let the current job considered is job k. Initially, k=1. Start with the job having earliest start time. Next assign the job with the next earliest start time, if possible without overlapping. Assign this job to the current machine, provided that (s_k , f_k) and (s_k+1 , f_k+1) are  such that s_k+1 ≥ fk. Continue assigning jobs to machine t  until all non-overlapping jobs are exhausted. Move the jobs assigned to a tabu list to prevent considering them further.

(1) Repeat step 2 for a new machine t. All the jobs assigned to machine t are moved to the tabu list.

(2) After each step, a new machine is used and the assigned jobs are moved to the tabu list. Continue this step until the tabu list is full. Then, the required number of machines is considered as the minimum number of machines required for the assignment of all jobs.

We need to compute a lower bound for the number of machines required to assign all the given jobs. This is done by looking at the amount of overlapping time intervals occur in each job. Even if there is even a minor overlapping, a job could not be placed in the same machine. So, we continue assigning separate machines for the jobs until zero overlapping occurs.

Here again, the algorithm starts by arranging the set of intervals in the ascending order of starting times.

We continue to build a list of jobs in such a way that there is some common overlapping interval for the jobs in the list. This could be achieved by placing jobs which satisfies the following conditions in the list of overlapping jobs. We try to find the maximum number of jobs with overlapping in a common time interval. This number can be considered as the minimum number of machines needed to assign all jobs.

Algorithm

(1) Arrange the intervals (s_j , f_j ) where s_j < f_j for j = 1, 2, ..,n, in the ascending order. Place the jobs in a new list.

(2) Start assigning jobs to machines from the new list. Let the current machine is t. Initially, t = 1. Let the current job considered is job k. Initially, k=1. Start with the job having earliest start time. Next assign the job with the next earliest start time, if possible without overlapping. Assign this job to the current machine, provided that (s_k , f_k) and (s_k+1 , f_k+1) are  such that s_k+1 ≥ f_k. Continue assigning machine to jobs until all overlapping jobs are exhausted. Move the jobs assigned to a tabu list.

(3) Repeat step 2 for a new machine t. All the jobs assigned to machine p are moved to the tabu list.

(4) After each step, a new machine is used and the assigned jobs are moved to the tabu list. Continue this step until the tabu list is full. Then, the required number of machines is considered as the minimum number of machines.

To illustrate the algorithm, let us consider a simple numerical example.

Let us assume that we are given a set of seven intervals of the form (s_j , f_j ). After rearranging the intervals in the  ascending order, suppose that we have the following set of intervals representing starting and finishing times of seven jobs.

(4, 10), (6, 9), (7, 11), (9, 16), (10, 16), (12, 15), [22, 29)

It is required to determine the minimum number of machines required to process all jobs.

It has been found that three machines are necessary.

Accordingly, jobs are assigned to the three are as follows:

Machine (1): (4, 10), (10,16), (22,29)

Machine (2): (6, 9), (9, 16)

Machine (3): (7, 11), (12, 15)

We can represent the above results by a Gantt Chart (Figure 1).

Figure 1. Gantt Chart representing the Machine Assignment for the Example

We start with the list of jobs arranged according to the ascending order of start times of jobs. Then we separate the list of jobs into several groups such that there exists a common overlapping interval into each group of jobs. The number of jobs in each group indicate the number of machines required to assign the jobs in the group. Let us illustrate this procedure by an example.

Group (1): (4, 10), (6, 9), (7, 11): 3 jobs: 3 machines Required

Group (2): (9, 16), (10, 16) : 2 jobs: 2 machines

Group (3): (12, 15) : 1 job: 1 machine

Group (4): (22, 29) : 1 job : 1 machine

Thus, the largest number of machines required for a single group of jobs is 3. Therefore, the lower bound for the number of machines required is 3.

Several test problems containing varying amount of jobs were generated with varying start times, finishing times, and having different job completion times. Situations where higher amounts and lower amounts of overlapping jobs were considered. It has been found that, when there were higher amounts of overlapping jobs, the number of required machines tend to become higher.

It has also been found that the lower bound of the number of machines required comes closer to the minimum number of machines when there are more free intervals among jobs which means that lesser amount of overlapping occurred.

The set of intervals containing jobs from 10 to 80 were considered.

The results are given below (Table 1).

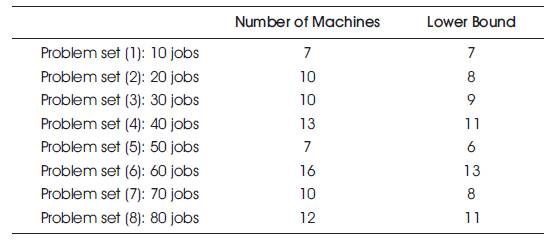
Table 1. Number of Machines Required and Lower Bounds for Test Problems

The graph indicating the number of machines required in each set of jobs and the relevant lower bound is given below (Figure 2).

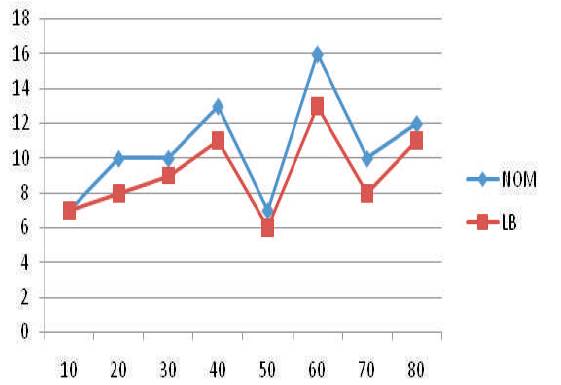
Figure 2. Number of Machines (NOM) Required and Lower Bounds (LB) for Test Data

To further refine the results we presented earlier, a larger set of test problems need to be constructed. However, from the above results it can be seen that, the minimum number of machines required to completely process a given set of jobs is very close to the lower bound of the number of machines. Hence, we can conclude that these results are close to the optimal and can be used for any practical purpose.