Now-a-days, accuracy of databases is much more important, as it is primary and crucial for maintaining databases in current IT-based economy and also several organizations rely on the databases for carrying out their day-to-day operations. This signifies the information quality ’s, importance, maintained in the form of databases, causing significant cost implications for a system that entirely depends on this information for its functioning.

While integrating the data, overlapping of the data from different sources will be the major problem, mentioned by Mayilvaganan, and Saipriyanha (2015), i.e., there may be a contradictory information from two or more sources for the same data. This may create a problem, as there is no certainty of the actual data from these two different sources, making the integration of data uncertain. In such a case, making a choice between data from different sources for taking into confidence, a particular data that represents the real world data, to integrate into the database will be required. For this there will be no fully automated system, making it a very laborious process, as it consumes time and money, and nearer to impossibility.

Basing upon their key fields, joining of various data or tables which are different is the basic mechanism in structuring a database, in which the data should be without any errors or duplications. As discussed earlier, this entry of a reliable data is not without any complications, as many things influence this ranging from entry of data that is free of any typographical errors to the duplication of data record. Hence, it becomes a crucial factor, for data cleansing, particularly in detecting the duplicate entries. However, this also not without any limitations as the huge data sizes in the current scenario are making this process of duplicate detection very expensive. Huge catalogues of a constantly emerging set of items offered by the online retailers from many different suppliers are the finest example of such a situation. Though duplication occurs whenever an independent person changes the product portfolio, online shops cannot afford to rectify this and the need for the duplication is unmet. Also that, to allow such an operation, there needs a unique, global identifier which the data often lacks.

In addition to these, S. Yan, et al. (2007) proposed to define the records from different places (sources), where reliable way is far from reality and to control the data quality. Many other elements influencing the correctness of the data are the errors in entering the data (e.g., Gogle in place of Google), lack of integrity constraints (e.g., lets entries such as Employee salary ¼ 567) and numerous ways of recording the identical information (e.g., 44 N. 4^th St. in place of 44 North Fourth Street), etc. and in some special cases like the underlying assumptions, difference in data is seen in the structure, semantics. The end result of all these, is compromising in terms of data quality.

Data Cleansing definition given by S. Sarawagi (2000) is the discovering and fixing the records which are inaccurate or corrupted within a set of tables, or records, or databases. And can also be done automatically by the person, where after reading the set of records, the accuracy will be tested. Usually, data cleansing make use of databases, and this covers many aspects of correction, ranging from identifying the irrelevant, incomplete, and inaccurate part of the data and then replacing, deleting or modifying that unwanted data.

Structural and lexical heterogeneity are the two main varieties of data heterogeneity identified by J. Widom (1995). While structuring the fields of the tuples in the database differently in different databases, Structural heterogeneity occurs. Though the tuples identically structured the fields across databases, if we refer to the data of the same real-world object by using different representations, Lexical heterogeneity arises.

Blocking and Sorted Neighborhood Method are very prominent algorithms stated by M. Herschel, and F. Naumann, (2010) which focus on the selection of pairs, and try to extend the efficiency, and are the most prominent algorithms in Duplicate detection.

Entity Resolution (ER) was proposed by Mie Miesu Thwin, and Aye Chan Mon (2013) where it uses two functions, match and merge. The match function classifies the duplicated records and the composite information about these matched entities is derived from merging function. Lack of unique identifiers for duplicate records, the major role of guesswork in determining the matching, expensive computations like using maximal common subsequences in two strings makes the identification of the matching records difficult.

For complex match strategies that contain several matchers, H. Kopche, et al. (2010) proposed a generic model for the parallel processing of these strategies. The parallel processing is based on the general partitioning strategies, which considers the memory and load balancing requirements. It involves the Cartesian product of input entities, in which partitioning the set of input entities is done, thus generating match tasks for each pair of partitions. As blocking is done instantly on the process and only the matching is executed in parallel, this remains as a main drawback of this model.

In the last few years, various Progressive Techniques evolved, stressing for the cost effective models, falling under this category are pay-as-you-go algorithms for information integration on large scale datasets, analysis of sensor data streams of progressive data cleansing algorithms, etc., none of which can be applied for duplicate detection.

A proposal that eases the problem of parameterization and progressively resolves the duplicates was made by Xiao, et al. (2009) for estimating promising comparison candidates, which involves a top-k similarity join using a special index structure. Although a list of duplicates will be made at the end, this model differs from the conventional ways, as it focuses on finding the top-k most similar duplicates, making it possible to identify duplicates in a given time and is irrespective of how long will this take by decreasing the similarity threshold.

“Hints” are the three kinds of progressive duplicate detection techniques introduced by Whang, et al. (2012) in the Pay-As-You-Go Entity Resolution. In this, in order to match more promising record pairs earlier than less promising record pairs; for the comparisons, hint defines a good execution order. But, we will miss the opportunity of adjusting the comparison order dynamically based on intermediate results at runtime, as all presented hints produce static orders for the comparisons, and this will be addressed by some techniques. Also, this approach calculates a hint only for a specific partition, that is a subset of records fitting into main memory, and goes on by completing one partition of a large dataset after another, thus making the overall duplicate detection process non progressive. By calculating the hints using all partitions, we can be able to partly address this. The algorithms presented in the proper use a global ranking for comparisons and the limited amount of the available main memory is considered. Another issue with this model is related to the proposed pre-partitioning strategy.

For preventing partitions from overlapping, the partitioning is made by using Minhash signatures. This doesn't mean that overlapping should be avoided completely, as the pair-selection is improved by this, algorithms are made to consider the overlapping blocks as well. For a completely progressive workflow, progressive solving of the multi-pass method and transitive closure calculation are essential, that are applied in this paper.

For more than five decades in statistics community, the problem that is arising is the record matching or a record linkage problem. To reduce the number of pairwise comparison and for increasing the effectiveness of pairwise comparison and also the number of unwanted comparisons has to be reduced for searching methods during de-duplication. To perform duplicate detection with high efficiency and effectiveness datasets, the two progressive algorithms are used to report most matches early on, while possibly slightly increasing their runtime. But this Sorted Neighborhood Methods (SNMs) are a standard indexing algorithm that sort dataset by using defined “sorting key” and in order to compare records which are within a window. So in addition to the existing work and also to get even faster results combing scalable approaches to the progressive approaches for finding the duplicates in parallel so as to deliver rapidly than the traditional approaches.

3.1 Progressive Sorted Neighborhood Method Algorithm

The PSNM algorithm has been implemented by Thorsten Papenbrock, and ArvidHeise, (2015) worked on appropriate partition size pSize, i.e., the end one in the archives using the unresponsive sampling function which outfits in the memory, calc Partition Size (D). To skip the window at their corresponding boundaries, the algorithm computes the total amount required for the partitions pNum. An assumption is made by storing the records, IDs in this array. PSNM is being proclaimed recsarray in order to stock the predefined records. Dataset D is classified by PSNM with the key K. Progressive sorting algorithm is used for sorting. Later, PSNM increases the window size regularly from 2 to end of the window size W by taking steps, I.

For all the progressive iterations, the entire dataset is studied at once by PSNM. The partition-wise, finishing of the load process continuously reiterated and loads all the partitions by PSNM. For the processing of the burdened partition, initially PSNM reiterates all the rank-distances which are presented in the interval, current window I. All the records at the current partition are recapitulated to their respective Dist-neighbor.

3.2 Progressive Blocking

With respect to the windowing algorithms, all pairs of the records existing in the group are compared after the assignment of each and every record to a particular group of identical records (the blocks). A latest methodology which is used to build an equidistant blocking technique is Progressive Blocking (PB) and is used for enlargement of blocks successively. Similar to PSNM, PB also sort the records previously and uses their respective ranks with respect to distance to estimate similarities in this type of sorting. Depending upon the sorting done, PB primarily creates and extends gradually a fine-grained blocking. The extended blocks are particularly executed around pre-identified duplicates on neighbors and enables PB in exposing clusters prior to PSNM.

4.1 Map Reduce

Google introduced MapReduce (2004), a model for programming in which parallel data-intensive will be supported in case of cluster computing environments. A MapReduce technique as discussed by E. Rahm, A. Thor, and L. Kolb (2011) involves Data partitioning and redistribution. By using Key, Value pairs, the entities will be signified. The two user defined functions which are used to compute are:

For Map, the function used is:

(Key , Value ) ->list (Key , Value )

For Reduce, the function used is:

(Key , list (Value )) ->list(Key , Value )

Sequential code exists in these functions and by utilizing the Data parallelism, these functions will execute in parallel. Processes like mapper and/or reducer are executed by MapReduce nodes.

Input partitions are scanned in parallel by Mapper processes and it will transform each entity is represented in a Key, Value pair earlier than the map function is executed which has been given by Jimmy Lin, and Chris Dyer (2010). Then, according to the key, the resultant of a map function will be sorted and the key will be repartitioned by applying the partitioning function. The partitions, i.e., all (Key, Value) pairs will be sent to each one node when they are redistributed. A receiving node maintains the static number of reducer processes. Then the reducer passes all values along with the same key to the reduce call in the Reduce phase.

4.2 Parallel SNM

Basing on the traditional Sorted Neighborhood Method discussed by Steffen Froedrich, and Wolfram (2010), Parallel SNM has been proposed. By using a predefined sorting key the input data is sorted, and the records which are in sorted order are alone compared within a window. The perception is that duplicate records will exist for those which are close in the sorted manner than the records which are far apart because with reference to their sorting key, they can be already similar. More precisely, the distance between two records in their rank-distance gives Parallel SNM an estimation of their matching probability. To vary the window size iteratively, the Parallel SNM uses this intuitive and to find the best promising records, a small window size of two can be started. By basing on the intermediate results (i.e., Look-Ahead), the Parallel SNM differs from other static approaches. Additionally, it processes considerably larger data sets by integrating a progressive sorting phase (i.e., MagPieSort).

4.2.1 Parallel SNM Algorithm

The implementation of Parallel SNM represented by the following algorithm takes five input parameters: D acts as a reference to the data, which has not yet been loaded from disk.

Algorithm 1: Parallel Sorted Neighborhood Method

Requirements: D, dataset reference; k, Sorting key; W, Window size; I, Enlargement interval size; N, Number of records.

 

In the step of Sorting, the sorting key, k is used which defines the attribute or the attribute combination. With correspondence to the traditional sorted Neighborhood Method, the W is used to specify the maximum window size. This parameter is set to a high default value when using the early termination. To define the enlargement interval for each progressive iterations, Parameter I is used. The number of records in the dataset is specified by the last parameter, N which is gleaned in the sorting step.

In general, the entire dataset cannot be fitted into the main memory. For this purpose, at a time the Parallel SNM runs over a partition. The parallel SNM calculates Psize, which is an appropriate partition size, i.e., maximum number of records which can fit in memory with the help of the pessimistic sampling function, Calcpartitionsize (D) which is represented in Line 2: the function calculates the record size of the data types and matches this for the available main memory which is read from the database. If not, it estimates the size of the record with accordance to the available main memory. In case of Line 3, the algorithm computes Pnum, which means the number of necessary partitions which considers a partition overlap of W-1 records which slides the window over their boundaries. The order-array is defined in Line 4; with regards to the given key K it stores the order of records. By assuming that it can be kept in a memory, this array stores only the record IDs. Parallel SNM states the rec array in Line 5 to hold the actual records of the current partition.

By using the Key K, the parallel SNM sorts the dataset in Line 6. This sorting is done by using Magpie method and the key is assigned to the windows parallel by basing on the method MapReduce which is discussed above. Then in Line 7, according to the steps of I, from window size 2 to the maximum window size W, the parallel SNM evenly increases. In this manner, close promising neighbors are selected at first and less far-way promising neighbors are selected later on. The parallel SNM reads the entire dataset once, after each of these iterations. As load process is done partition wise, Parallel SNM iterates (Line 8), and loads all the partitions (Line 9) in parallel. In order to process the loaded partition, Parallel SNM iterates all the record rank-distances dt first which are within the I , known c as Current Window interval. This will be only one distance for I=1, i.e., the current main-iteration record rankdistance. Then in order to compare them with their dtneighbors, the Parallel SNM iterates over all records within the current partition. In Line 13, by using comparatives (pair), the comparison will be executed. It is said to be a duplicate, when this function returns "True".

When comparing the proposed approach with the PSNM, the performance evaluation is discussed in this section. The graph signifies the performance measurements of proposed algorithm plot of the total time taken for detecting the duplicates over the PSNM. Here each and every duplicate is the positively matched record pair. In case of graphs, it is manually marked with some points from hundred measure data points which makes a graph.

In this paper, the CD dataset is considered in examining the performance of proposed algorithm which comes with an own true gold-standard.

The characteristics of the CD-dataset are given in Table 1. The CD-dataset records are about music and audio CDs, mainly focused on increasing the efficiency by maintaining the same effectiveness.

Table 1. CD Dataset with its Characteristics

Hence, assuming the correcting measure; treating like an exchangeable black box. However, the Damerau- Levensheitn similarity is used for experiments which mentioned above and on the CD-dataset, where the precision of about 93% is achieved by the similarity value.

5.1 Metrics

This section defines a novel metric for measuring efficiency over the time and also the metric that is used for detection of duplicates. This paper focuses on recall description given by Karl Goiser, and Peter Christen (2007),but not the precision because it is a similarity function.

The distinct sampling function is:

(1)

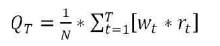
Where, N has referred to a dataset, it is the total amount of duplicates, r_t is used to know the arise number of duplicates, w_t is used to define as the weighting function signified over the time, Q_T is the quality of duplicate detection for T which is the measurement.

5.1.1 Damerau-Levensheitn Similarity

A string metric, namely the Damerau-Levensheitn similarity is used here for experiments and on the CDdataset. Levensheitn similarity is to evaluate the difference between the two strings (or texts) or sequences.

Levensheitn similarity distance is also named as Edit- Distance described by Jalaja, G., and Veena (2015). The three operations those can be made are Substitution, Insertion, and Deletion.

In a belief that there exists the bigger return value if the strings are less similar to the reason that rather than similar strings (or texts) needs less edits than the different strings (or text).

Let us consider M and N strings used to evaluate the Edit- Distance mathematically shown as:

(2)

5.2 Results

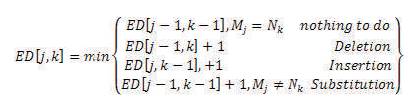
In this work, the CD dataset is considered as shown in Table 2 for examining the performance of proposed algorithm which has the details about the music where it has different attributes like different tracks, title of Disc, genres, etc. In this work, the method of Parallel SNM is applied to the dataset in such a way that is discussed as below:

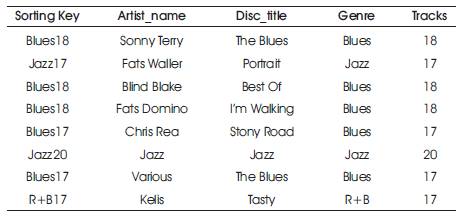
Table 2. Dataset by adding Sorting Key

Step 1: The dataset will be sorted as that of the process of traditional sorted neighborhood method. The Sorting key has to be calculated by basing on the attributes that is presented in the respective dataset.

For example, let us consider some of the attributes that are taken from the dataset: Name of the artist, title of Disc, Genre, and Track. For instance, selecting the key for sorting here is said it be “Genre + Track”.

In the ongoing process, the window will be sliced on the records in a sequence. Let us apply this to the example taken. Where, Window size, w=3 and Row count, n=9. Then,

(3)

Step 2: Input partitions are scanned in parallel by Mapper processes and it will transform each entity represented in a Key, Value pair earlier than the map function is executed.

Step 3: Now the key will sort according to the output of a map function and by applying a function of the key called, “partitioning” function. It will be repartitioned. Different keys are taken for partition, but in the same partition all the values are in the same key. Then it is redistributed by the partitions, i.e., the partition with all Key, Value pairs are sent to one node exactly.

Step 4: Now the output of Map function will be transferred to reduce phase as shown Table 3, and Table 4. Then the number of processes which are fixed will be hosted by the receiving node, whereas for handling the output pairs of map from all mappers where the same key is shared is handled by a single reducer. Where the receiving node maintains the static number of reducer processes. At this juncture, with the same key, all the values will be passed over the reducer in the reduction phase by a reduce call. Then the reducer passes all values along with the same key to the reduce call in the Reduce phase.

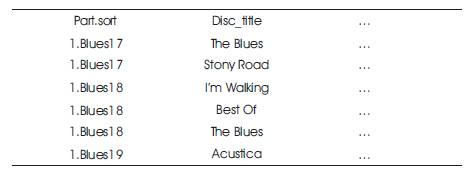
Table 3. Reduce Phase1

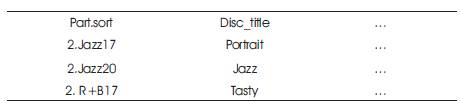
Table 4. Reduce Phase 2

5.3 Experimental Setup

Figure 1 shows the curves of the time for processing corresponding to the previous curves. To illustrate the behavior, the graph is assessed by altering the size of the window for the CD-dataset for which the true goldstandard has given. The curves give the following insights: which one of them underlines the processing time of PSNM and another one underlines the Parallel SNM.

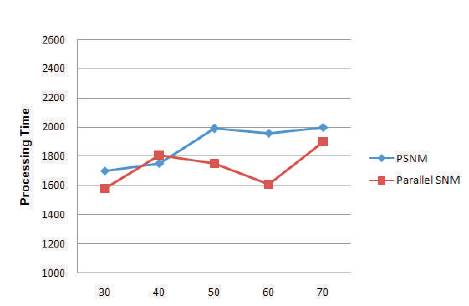
Figure 1. Window Size vs Processing Time

Figure 2 shows the curves of the time for processing corresponding to the sorting key that is selected over the records. The curves give the following insights: which one of them underlines the processing time of PSNM and other one underlines the Parallel SNM.

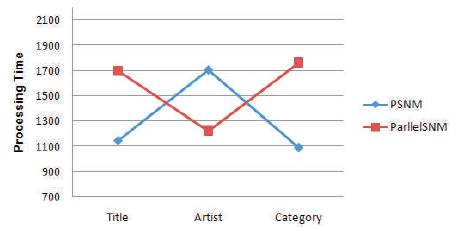
Figure 2. Sorting Key vs Processing Time

The curves give the following insights: which one of them underlines the processing time of PSNM and another one underlines the Parallel SNM.

This paper introduced the Parallel SNM, where it is found that the throughput and efficiency of duplication detection has increased. Within a limited execution time, it is observed that this algorithm increases the efficiency of duplicate detection; where basing on the intermediate results obtained to execute the close promising are selected at first for comparisons and less far-way promising neighbors are selected later. For the determination of the performance gain of the proposed algorithm, this paper also presented a novel quality which integrates the existing measures. In order to interleave their progressive iterations, it uses multiple sort keys in parallel. At runtime by examining the intermediate results, dynamically ranking the different sorting keys, drastically easing the problem of key selection and by overcoming the key selection problem can result a better evaluation of the duplicate detection are considered as a future work.