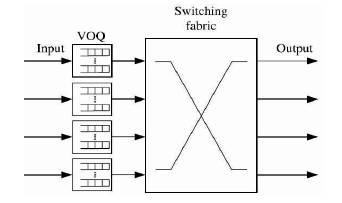
Figure 1. NxN Input Queued Switch Architecture
The increasing use of multicast applications on the internet, has an urgent need for the high speed router/switches, which handles the multicast traffic efficiently. The core component of the router is the switch fabric. The scheduling algorithm which configures the switch fabric to arbitrate and transfer the cells between the input and output ports. Most of the existing multicast scheduling algorithms performed well under uniform traffic, but failed to achieve maximum throughput under non-uniform traffic. In this paper, the authors have proposed a multicast scheduling algorithm called Enhanced Multicast Due-Date Round Robin Scheduling Algorithm (E-MDDR), which got the improved throughput compared with Multicast Due-Date Round Robin Scheduling algorithm (MDDR). Since E-MDDR computes the residue of the cells waiting until M cell times and those cells are declared as the emergency cells, which are transferred between every M time slot for an NxM switch. So that it achieves the improved throughput and minimum delay under non-uniform Bernoulli and bursty traffic patterns.
In the recent internet world, due to the huge amount of internet users, we consider the multicast support to the high speed routers/switches. Input Queued (IQ) switch architecture is well suitable to support the multicast traffic because it requires no speedup. Furthermore, IQ switches need the scheduling algorithms to configure the switch fabric. The switch fabric is the core component of the router/switches which is multicast enabled that one input port can connect with atmost N output ports, but one output port can receive atmost one cell at a time slot.
So many unicast scheduling algorithms have been proposed for IQ switches, which achieves 100% throughput under both uniform and non-uniform traffic patterns. But few multicast scheduling algorithms have been proposed for IQ switches. TATRA [1] is the conventional multicast scheduling algorithm which mainly use the single FIFO (First In First Out) queue to store both unicast and multicast cells and which severely suffer from the HOL (Head-of-Line) blocking problem for its single queue nature. Also, it failed to achieve the maximum throughput under non-uniform traffic patterns. To avoid the HOL blocking, Virtual Output Queues (VOQs) for multicast traffic have been proposed by McKeown [2]. VOQs avoid Head-of-line (HOL) blocking to a large extent, but the issue with such a queueing scheme is that, it is impractical to maintain all the possible VOQs corresponding to all the outputs. Whereas other algorithms [7], [8] maintain a number of FIFO queues in each input port to reduce the HOL blocking problem. This queuing architecture is known as K-MC-VOQ and theoretically, the performance of those are analyzed in [10]-[14]. ESLIP [3] uses the VOQ structure to store the unicast cells and one single queue to store the multicast cells and its a variant of iSLIP algorithm. As expected, ESIP eliminates HOL blocking for unicast traffic and not multicast traffic.
FIFOMS [4] is the integrated scheduling algorithm which does not suffer from HOL blocking. It effectively uses the multicast capability of the crossbar switch fabric. It achieves 100% throughput under the uniformly distributed traffic but not for non-uniform traffic.
MDRR [5] is round-robin based multicast scheduling algorithm with operates on two phases-request and grant. Each and every input port maintains two pointers. The usage of pointer is very cost effective. It can't achieve maximum throughput under non-uniform traffic pattern.
In [9], Multicast Due Date Round Robin (MDDR) scheduling algorithm, the authors have achieved well under both uniform and non uniform traffic pattern. Still it has throughput degradation that the residue of some of the cells are waiting for more than N time slot, where N is the number of output ports or the maximum fan-out size. In this paper, the authors have proposed the E-MDDR scheduling algorithm which overcome the waiting cells in the VOQ by announcing it as the emergency and M+1 time slot is allotted for these cells to transfer completely. It mainly minimizes the average cell delay and achieves the maximum throughput.
In this paper, the authors have analyzed the throughput performance of the E-MDDR Scheduling algorithm. The rest of the paper is organized as follows. In section 1, the authors defined the packet switch architecture. In section 2, E-MDDR algorithm has been proposed. In section 4, Performance evaluation and result analysis have been presented. Finally, the authors have concluded the paper.
The multicast scheduling algorithm configures the switch fabric for arbitrates between the input and output ports. Based on the arbitration, the cells are transferred. The variable length packets are splitted into equal size cells. Here, fan-out splitting [6] scheme is adopted to transfer the cells in various time slots. Any multicast cell characterised by its fan-out set, describes the number of destinations that the cell is destined for. The residue is the remaining cells form a fan-out set which are not transferred in the previous time slot. To improve the fairness, the residue is concentrated to transfer time slots as early as possible . Figure 1 shows the NxN Input-Queued switch architecture, which has a switch of N input ports and N output ports, and the switch fabric is the core component of the switch which is connects the input and output ports for any time slot. A number of VOQ's which are dedicated to each input port is defined as a term 'k'.

Figure 1. NxN Input Queued Switch Architecture
Based on the traffic pattern, multicast cells are arrive, which are partitioned into k queues according to the distribution. The arbitration is happened based on the scheduling algorithm. Each input port is connected with the at most N outputs and each output port is connected to at most one input. Until, all the destinations of the cell is reached, the cell is retained in the queue. If its fully served, then its removed from the HOL position of the queue.
In this section, the authors have proposed the Enhanced Multicast Due Date Round-Robin Scheduling Algorithm (EMDDR). It works under the request and grant phases. This algorithm concentrate on the residue of the cells waiting for more than M cell times.
For any non-uniform traffic,
I. Input ports are prioritized based on the cells which is having the highest fan-out size.
ii. Priority order of the input ports are iterated one-by-one.
iii. Every input port selects the queue based on the highest fan-out.
iv. Due dates are assigned to the fan-out cells in the current queue of the current input port.
v. For each due date the unassigned cells set due date 1 to priori non-exist cell, and 2 to priori exist cell.
vi. Make request for the 1st due date cells to the output ports.
vii. If output port receives more than one request, choose one from the global pointer points and grant it.
viii. If output port receives only one request, it directly grants it. Repeat the iteration with the non-granted cell requests and remaining fan-outs further.
The authors have implemented the simulation model in NS2 that models the NxN Input-Queued switches. In general, for all the experiments they have used the 8x8 and 16x16 Input-Queued Switches. The Bernoulli non-uniform and bursty non-uniform traffic patterns are used.
A time slot is the unit of time to make arbitration to transfer packets from input ports to output ports. Slots are numbered 0,1,2,3… and the IQ switch starts to run at time slot 0.
Performances of the proposed work are computed using the delay and throughput achieved. A multicast cell is stored in the queue until all the destinations in its fan-out set are reached. The multicast delay of a cell is calculated as the cell times that the cell stays in the queue until it is removed. Delay is increased when they become unstable as the offered load increases.
Throughput is the another performance measurement used in this investigation, which is defined as the ratio between the total number of cells forwarded to output interfaces, and the total number of cells arrived at input interfaces. It is essentially a measure of the cell loss probability at input queues. In this proposed work, the authors have compared their work with the MDDR algorithm and could judge, that proposed work has got the improved throughput than the existing work. The delay-throughput performance of E-MDDR and MDDR schemes have been well demonstrated under two non-uniform traffic conditions.
The authors first applied the Bernoulli non-uniform traffic to the 8x8 switch. Figure 2 shows the load-delay performance of the MDDR and E-MDDR algorithms. The input load is varied from 0 to 1.0. For the load upto 0.8, both algorithms maintain almost an equal delay. At higher offered load, E-MDDR achieves a minimum delay compared with MDDR.
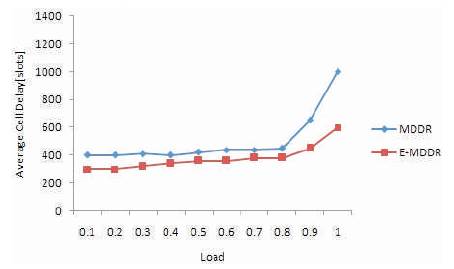
Figure 2. Average Cell Delay as a Function with respect to Load for Bernoulli Non-uniform Traffic
Figure 3 shows the throughput performance of E-MDDR and MDDR under Bernoulli non-uniform traffic. For load upto 0.5, both algorithms achieved greater a throughput greater than 90%. For the load increasing above 0.8, MDDR throughput is degraded to below 80%.
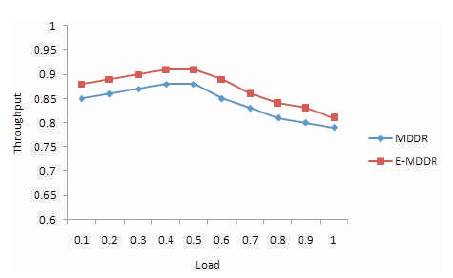
Figure 3. Throughput as Function with offered Load for Bernoulli Non-uniform Traffic
Figure 4 shows the simulation results when Bursty non-uniform traffic is applied. Figure 4 compares the average multicast delays under various traffic loads. For bursty traffic also, when the load is increased, E-MDDR achieves a minimum delay compared to MDDR.
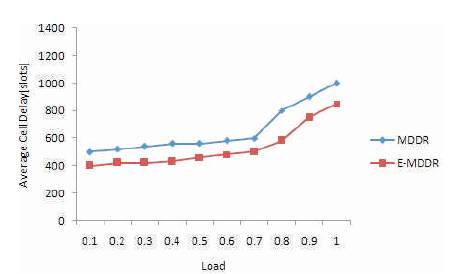
Figure 4. Average Cell Delay as a function with respect to Load for Bursty Non-uniform Traffic
Figure 5 shows the throughput performance of E-MDDR and MDDR under Bursty non-uniform traffic. For load 0.4, MDDR got 80% of the throughput but E-MDDR achieved above 90% of the throughput. For the load increasing above 0.5, MDDR throughput is degraded to 75%, but EMDDR maintains the throughput in the range of 85%.
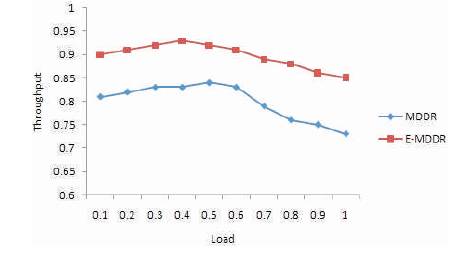
Figure 5. Throughput as Function with offered Load for Non-uniform Bursty Traffic
Fan-out is another factor which influences the switch throughput. Figure 6 shows the throughput performance of E-MDDR when the fan-out is increased. E-MDDR achieved the higher throughput than MDDR. Since, fanout splitting disciple is applied for cell transmission.
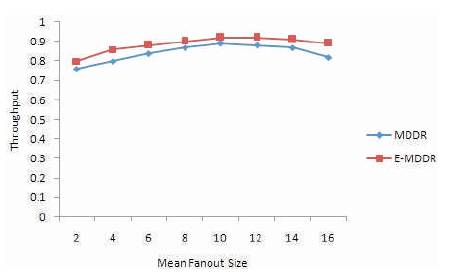
Figure 6. Throughput as function of mean Fanout size for Non-uniform Traffic
Figures 7 and 8 show that the throughput performance of E-MDDR and MDDR with respect to load for the burst lengths 4, 8 and 16 under Bernoulli non-uniform traffic. When the burst length is high, MDDR has a poor throughput, but E-MDDR achieves a maximum throughput, since every M time slot emergency cells are arbitrated by E-MDDR. This lead to increase the throughput.
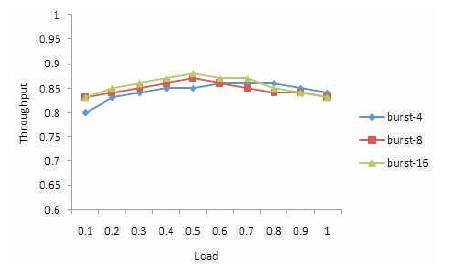
Figure 7. Throughput as function with respect to load for MDDR with various Burst length under Bernoulli Non-uniform Traffic
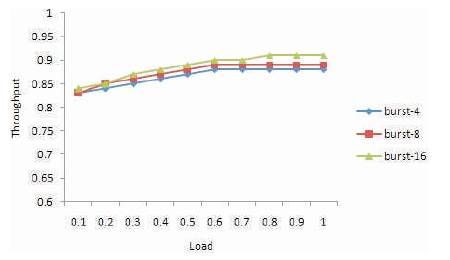
Figure 8. Throughput as function with respect to load for E-MDDR with various Burst length under Bernouli Non-uniform Traffic
The future work includes implementing the E-MDDR algorithm for the integrated environment [12] which supports both unicast and multicast scheduling.
In this paper, the authors have modified the MDDR algorithm as Enhanced Multicast Due Date Round Robin scheduling algorithm, which concentrates on the residue of the cell transfers between every M cell time. This leads to increased throughput and minimum delay under nonuniform traffic pattern and also concludes that when the burst length is high E-MDDR achieves a maximum throughput. So, the current work is enhanced to reduce the waiting time of the residue cells and achieve the maximum throughput in the input-queued multicast switches.