Multipliers play a vital role in majority of the processorbased digital systems, digital signal processing arena, digital communications, spectrum analysis and digital filtering zones. Most of the high performance systems like microprocessors, digital signal processors, etc., include complex multipliers circuits that operate at highest system clock rates. Over 70% of the instructions in various DSP algorithms and microprocessors are comprised of different adders, multipliers and MAC units. The delay parameters associated with these units form the crux in satisfying overall design constraints. Therefore the demand for high-speed processing is tremendously increasing in view of the expanded usage of complex and high-speed multiplier architectures in various applications.

The main objective of Electronic Design Automation (EDA) process is aimed at computerizing entire VLSI design process through number of emerging EDA tools in order to convert HDL design representations into Application Specific Integrated Circuits (ASICs). The global EDA giant companies are also continuously delivering high end automation tools like Cadence Design Systems, Magma Design Automation, Xilinx, Mentor Graphics, Synopsis, etc., for designing electronic systems and integrated circuits. The proposed work is mainly based upon the usage of Mentor Graphics (CMOS-130 nm) technology to experimentally implement Baugh-Wooley and 4 bit Wallace- Tree multiplier architectures. The proposed work is carried out in Complementary Metal Oxide Semiconductor (CMOS) 130 nm technology satisfying various design constraints.

Power management is a pre-dominant factor of concern in various audio-video digital signal/image processing VLSI systems, depending on the computational speed and processing abilities of multipliers employed. Amanollahi and Jaberipur (2017) proposed the design of sequential multipliers using radix-16 CSA (Carry-Save Adders) to generate accumulated partial product. Evaluated results depicted improved latency, power dissipation and energy consumption at the cost of additional silicon area. Antelo et al. (2016) discussed about the optimized binary radix-16 (modified) Booth multipliers to allow optimization of partialproduct- array stage in terms of area/delay/power. The method is extended to radix-8 multipliers, signed/unsigned multipliers etc. Qiqieh et al. (2018) proposed a Significance- Driven Logic Compression (SDLC) approach based on bit significance to form a reduced set of partial product terms. Various parallel multiplication schemes are used to reorganize the designs. Anuar et al. (2010) proposed a twophase clocked adiabatic static CMOS logic circuit based on the principles of adiabatic switching and energy recovery. This architecture can be used in low-power digital devices such as RFIDs (Radio-Frequency Identifications), smart cards, and sensors.

Tang et al. (2017) proposed a 4-bit bit-slice integer multiplier using both signed and unsigned multiplications. The obtained results depict the operation of the multiplier at a throughput of 3.125 × 109 multiplications per second. Moss et al. (2018) presented a radix-4 multiplier suitable for digital filters, artificial neural networks, and other machine learning algorithms. Design is evaluated on an Intel Cyclone-V FPGA (Field-Programmable Gate Array). Performance of multiplier can be improved by the distribution of bit representations. Karthikeyan et al. (2018) proposed implementation of 32-bit Baugh-Wooley multiplier, evaluated in Xilinx ISE 14.5 tool – design is comprised of half adders and full adders. Results clearly deployed a reduction in silicon area and transistor count. Yengade and Indurkar (2017) discussed the implementation of 32 bit Baugh-Wooley multiplier. The design is evaluated using the XILINX ISE 14.5 tool. The power consumption and delay parameters obtained are found superior to the existing ones. Kumawat and Sujediya (2017) proposed a reconfigurable 8 x 8 Wallace Tree multiplier using CMOS and GDI technology. The main idea of implementation is to generate partial products in parallel using AND gates. Significant reduction in power consumption, silicon area and transistor count are observed. Wallace – tree based multipliers provide area efficient strategies for high speed multiplication.

Tiwari (2013) highlights the implementation and verification of low power multiplier and its analysis on reconfigurable devices. Mathew et al. (2013) implemented a design and analysis of an array multiplier using an area efficient full adder cell in CMOS Technology. Alaoui (2011) experimented with design and simulation of a modified architecture for carry save Adder based multiplier. Chandel et al. (2013) discussed about ease of doing multiplication with booths multiplier. Bewick, (1994) and Kuang et al. (2009) discussed about fast multiplication algorithms and implementation.

As a fundamental arithmetic operation, multiplication includes various algorithm-level and bit-level computational features that are not at all considered for low-level power optimizations. The efficiency of today's VLSI systems is totally reliant on the performances of inherent multipliers and computational methodologies adopted. Different serial and parallel high speed multiplier architectures are employed for innumerable number of computing applications, where the area of any multiplier is quadratically related with the operand precision; On the other hand, parallel multipliers have complex architectures and have many logic levels that introduce spurious transitions (or glitches). The structure of parallel multipliers is complex enough to achieve high speed and even deteriorates the efficiency of layout and hinders the circuit level optimization. Therefore, it is very essential to develop algorithm level and architecture level power optimization techniques. To ensure fast multiplication operations, some of the techniques such as Shift and Add Multiplier, Combinational Multiplier, Array Multiplier, Carry Save Adder Multiplier, Booth's Multiplier, Modified Booth's Multiplier, Grid Multiplier, Lattice Multiplier, Vedic Multiplier, Wallace-Tree Multiplier, Baugh-Wooley Multiplier, etc., are employed. Adder circuits and Multiply Accumulate Carry (MAC) units form the crux design units in almost all the multiplier circuits. Over the past few years, researchers have proposed the various modifications of multiplier designs to optimize power consumption, area and enhance the speed as well. Few of the multiplication algorithms are discussed below for further extrapolation.

• Shift-and-Add Multiplier: Shift-and-add multiplication adds the multiplicand X to itself Y times, where Y denotes the multiplier. To multiply two numbers, digits of the multiplier are taken one at a time from right to left, multiplying the multiplicand by a single digit of the multiplier and placing the intermediate product in the appropriate positions to the left of the earlier results.
• Combinational Multiplier: Multiplying two unsigned (or signed) binary numbers, each bit of the multiplier is multiplied against the multiplicand, and the product is associated according to the position of the bit within the multiplier, and resulting products are added to form the final result. The main advantage of binary multiplication is that the generation of intermediate products are easy.
• Array Multiplier: Array multiplier is well known due to its regular structure. Multiplier circuit is based on add and shift algorithm. Each partial product is generated by a multiplication of the multiplicand with one multiplier bit. The partial products are shifted according to their bit orders and then added. Addition can be performed with normal carry propagate adder. N-1 adders are required, Where, N is the multiplier length. Major limitation of array multiplier is its size. As the operand sizes increase, arrays grow in size at a rate equal to the square of the operand size.
• Carry Save Adder: Carry save adder is used to compute the sum of three or more n-bit binary numbers. A carry-save adder differs from other digital adders, in which it outputs two numbers of same dimensions as the inputs, one is a sequence of partial sum bits and another is a sequence of carry bits. If the adder is required to add two numbers and produce a result, carry-save addition is useless, since, the result has to be converted back into binary and carry bits need to propagate from right to left.
• Booth Multiplier: Booths Algorithm is a smart move for multiplying signed numbers. It utilizes 2's complement notation of signed binary numbers for multiplication.
• Modified Booth's Multiplier: In modified Booth's multiplication algorithm, three multiplier bits are examined at a time. In comparison with the original Booth's algorithm, which examines two bits at a time, the modified algorithm requires half the number of iterations at the cost of increased complexity for each iteration.
• Baugh-Wooley and Wallace-Tree multiplier: Architectures are left for experimentation in the remaining sections of the manuscript.

2's complement is the most popular method of representing signed integers, where negation represents negative numbers using 2’s complements. Baugh-Wooley's 2's complement algorithm for multiplication of signed numbers is famous for its ability to maximize the multiplier's regularity and to allow every partial product to have bits of positive sign. Baugh-Wooley algorithm was developed to design straight (direct) multipliers for 2's complement numbers.

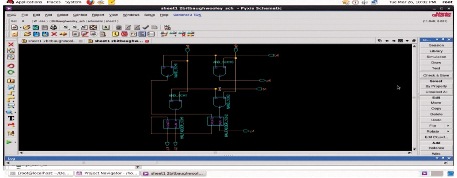
In case of directly multiplying 2's complement numbers, all of the added partial products are signed numbers, each of them are sign extended to fit with the width of final product, thereby formulating the right value of sum through Carry Save Adder (CSA) tree. Baugh-Wooley algorithm provides an efficient method of dealing negatively weighted bits in partial products by adding extra entries in the partial product matrix. Schematic diagram of 2 bit Baugh-Wooley multiplier is depicted in Figures1 to 3.

Figure 1. Simulation Setup of 2 Bit Baugh-Wooley Multiplier

Figure 2. Output Waveforms of 2 Bit Multiplier with a0=1, a1=1, b0=1, b1=0

Figure 3. The 4-Bit Product Values P3 P2 P1 P0

4. Experimental Analysis of 4 Bit Baugh- Wooley Multiplier

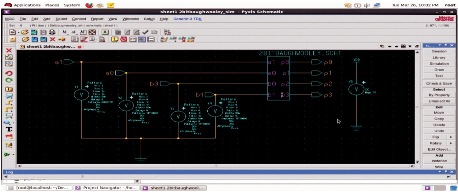
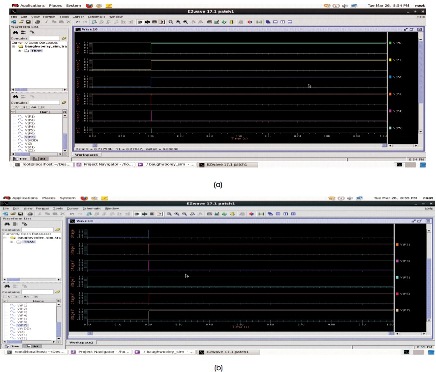
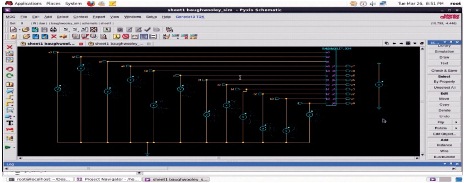
Schematic diagram and simulation setup of 4-bit Baugh-Wooley multiplier architecture is depicted in Figure 4.

Figure 4(a,b). Experimental Analysis of 4 Bit Baugh-Wooley Multiplier

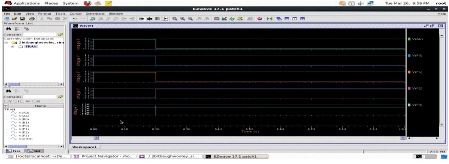
Output waveforms for multiplication of two 4-bit numbers a=4, b=2 are shown in Figure 5. Figures clearly illustrate the increase in hardware, including the number of adders used, owing to the increase in bit size of input numbers to be multiplied.

Figure 5 (a,b) Output Waveforms of Multiplication

5. Implementation of 4 Bit Wallace Tree Multiplier

Wallace-Tree multipliers are basically intended to handle multiplications of large operands by minimizing the number of partial product bits fastly and efficiently by means of carry save adder tree comprised of one bit full adders, where pseudo-adders are used to add the three inputs, and produce two outputs whose sum is equivalent to addition of all the three inputs. Here, several pseudo adders are used concurrently in order to minimize carry propagation and to enhance the speed of multiplication. Wallace-Tree approach minimizes the partial products by having numerous number of input compressors, in concurrence with the resultant delay being proportional to log n (for n number of rows) and accumulating quite a lot 3/2 of partial products in tandem. The entire process of multiplication is summarized below,

• After the generation of partial products, set of counters minimizes the partial product matrix without propagating the generated carry's.
• Another set of counters further reduces the matrix to continue the entire process and generate a two- row matrix.
• Two rows get summed up with final carry propagate adder. This method derives advantage of CSA to avoid carry propagation until the final adder.
• Wallace-Tree algorithm holds few irregularities in layout, as it comparatively contains complex interconnections.

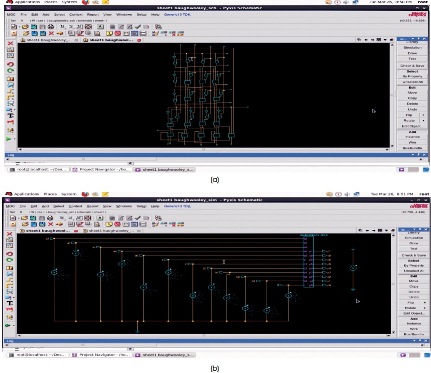
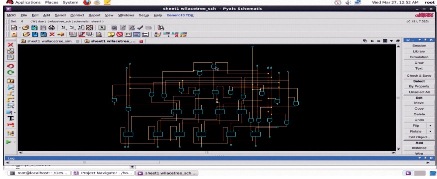
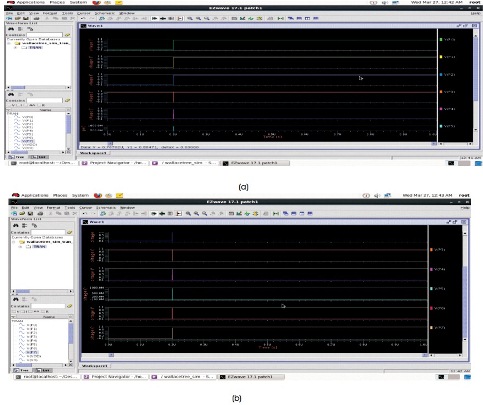
Schematic diagram of 4-bit Wallace-Tree multiplier is depicted in Figure 6. Simulation setup for 4-bit Wallace- Tree multiplier is depicted in Figure 7. Output wave forms for a=4, b=-2 are depicted in Figure 8.

Figure 6. Schematic Diagram of 4 - Bit Wallace - Tree Multiplier

Figure 7. Simulation Setup of 4 - Bit Wallace - Tree Multiplier

Figure 8. (a,b) Output Waveforms

6. Comparative Analysis of Proposed Architectures

A relative analytical study of 4 bit Baugh-Wooley and Wallace-Tree multiplier architectures are better understood by means of Table 1 depicted.

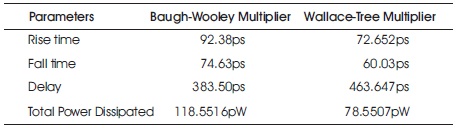
Table 1. Comparative Analysis of 4-bit Baugh-Wooley and Wallace-Tree Multiplier

Henceforth, it was observed that by considering all the parameters, both designs are found significant with each other. However, observations clearly reveal the technical superiority of Baugh-Wooley multiplier over Wallace-Tree multiplier by means of lesser delay values. The total power dissipated by Baugh-Wooley circuit is more than the Wallace-Tree multiplier. The rise time and fall time values of Baugh-Wooley multiplier are observed to be less relative to the Wallace-Tree multiplier.

Conclusion

Based on the calculations relevant to switching process and implicated analysis overhead in transistors, it was observed that Wallace-Tree multiplier exhibits less power dissipation compared to Baugh-Wooley multiplier. Therefore, experimental analysis concludes that Baugh- Wooley multipliers are more preferred for less denser packaging circuit applications producing results with reduced latency values. However, Wallace-Tree multipliers are suitable for high density packaging circuit applications. Thereby, producing better results due to lesser power dissipation.

The proposed architectures can be further modified to minimize the propagation delay values. Even though the proposed works are executed by using 130nm CMOS technology device sizes, it can still be scaled down to the nano-meter range of scales to exploit enhanced performance levels. Though the designs include basic arithmetic blocks like Full Adder, Half Adder, etc., they can be modified through Carry Save Adder, Ripple Carry Adder etc. The circuits can also be implemented using adiabatic static logic. Performances can be studied by varying widths of transistors. Wherever speed of operation is needed, a reduction in a number of logic levels may improve the performance levels, thereby decreasing the delay values and enhancing the speed of propagations involved.

References

[1]. Alaoui, C. (2011). Design and simulation of a modified architecture of carry save adder. International Journal of Engineering (IJE), 5(1), 102-113.

[2]. Amanollahi, S., & Jaberipur, G. (2017). Fast energy efficient radix-16 sequential multiplier. IEEE Embedded Systems Letters, 9(3), 73-76. https://doi.org/10.1109/LES. 2017.2714259

[3]. Antelo, E., Montuschi, P., & Nannarelli, A. (2016). Improved 64-bit radix-16 Booth multiplier based on partial product array height reduction. IEEE Transactions on Circuits and Systems I: Regular Papers, 64(2), 409-418. https://doi.org/10.1109/TCSI.2016.2561518

[4]. Anuar, N., Takahashi, Y., & Sekine, T. (2010). Two phase clocked adiabatic static CMOS logic and its logic family. JSTS: Journal of Semiconductor Technology and Science, 10(1), 1-10.

[5]. Bewick, G. W. (1994). Fast multiplication: Algorithms and implementation (Doctoral dissertation), Stanford University.

[6]. Chandel, D., Kumawat, G., Lahoty, P., Chandrodaya, V. V., & Sharma, S. (2013). Booth multiplier: Ease of multiplication. International Journal of Emerging Technology and Advanced Engineering, 3(3), 118-122.

[7]. Karthikeyan, A., Sumathi, K., Nivash, V. S., Logeshwaran, K., & Rajkumar, R. P. (2018). An efficient VLSI implementation 32-bit Baugh-Wooley multiplier. International Journal of Creative Research Thoughts (IJCRT), 6(1), 802-805.

[8]. Kuang, S. R., Wang, J. P., & Guo, C. Y. (2009). Modified booth multipliers with a regular partial product array. IEEE Transactions on Circuits and Systems II: Express Briefs, 56(5), 404-408. https://doi.org/10.1109/TCSII.2009.2019334

[9]. Kumawat, P. K., & Sujediya, G. (2017). Optimize circuit and compare of 8 x 8 wallace Tree Multiplier using GDI and CMOS technology. International Journal of Advanced Engineering Research and Science, 4, 20-24. https://doi.org/10.22161/ijaers.4.7.3.

[10]. Mathew, K., Latha, S. A., Ravi, T., & Logashanmugam, E. (2013). Design and analysis of an array multiplier using an area efficient full adder cell in 32 nm CMOS technology. International Journal of Engineering and Science, 2(3), 8- 16.

[11]. Moss, D. J., Boland, D., & Leong, P. H. (2018). A twospeed, radix-4, serial–parallel multiplier. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 27(4), 769- 777. https://doi.org/10.1109/TVLSI.2018.2883645

[12]. Qiqieh, I., Shafik, R., Tarawneh, G., Sokolov, D., Das, S., & Yakovlev, A. (2018). Significance-driven logic compression for energy-efficient multiplier design. IEEE Journal on Emerging and Selected Topics in Circuits and Systems, 8(3), 417-430. https://doi.org/10.1109/ JETCAS.2018.2846410

[13]. Tang, G. M., Takagi, K., & Takagi, N. (2017). 32× 32-bit 4-bit bit-slice integer multiplier for RSFQ microprocessors. IEEE Transactions on Applied Superconductivity, 27(3), 1-5. https://doi.org/10.1109/TASC.2017.2662700

[14]. Tiwari, G. (2013). Analysis, verification and FPGA implementation of low power multiplier. International Journal of Research in Engineering and Technology (IJRET), 2(3), 220 - 224.

[15]. Yengade, K. S. N., & Indurkar, P. R. (2017). Design of low power Baugh-Wooley multiplier. International Journal for Research in Applied Science & Engineering Technology (IJRASET), 5(7), 813-817.