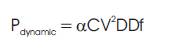
To design the computing system, energy efficiency is an important issue to be considered. Approximate computing has been evolved as an optimistic solution for energy efficient design of digital systems. While designing these systems, power dissipation is the significant issue for integrated circuits in nanometric Complementary Metal Oxide Semiconductor (CMOS) technology. Approximate implementations of a circuit have been considered as a potential solution for applications in which exact result is not required, which eventually reduces power consumption. The approximate computing has various research activities which varies from programming languages to transistor levels. Here, different approximate adder circuits have been reviewed, which are based on XOR and XNOR gates, and majority gates. Where emerging nanotechnology exploit these majority gates, combining with approximate computing gives the potential to reduce power consumption. Approximate circuit provides low power consumption, low transistor count, less area and reduced delay. Hence it is a good option, when strict exact solution is not required. This paper is about the survey on arithmetic circuits and different design topologies such as Logic, Nanomagnetic Logic (NML) logic.
A rising number of applications such as media processing, data mining and recognition, demands for energy-efficient designs for computation. Circuit designing and power dissipation have been important issues for integrated circuit design in nanometric CMOS technology. To reduce power consumption, approximate circuits have been considered as a potential solution for applications, where exactness is not required. Thus approximate computing techniques relax accuracy in order to improve both performance and/or energy consumption savings.
A huge number of digital circuits used adders as basic building blocks in aforementioned applications. Addition is a fundamental arithmetic operation. Adders have been investigated for approximate implementation which are not only used for addition, also used for subtraction, multiplication and division. The basic purpose of this paper is to review the arithmetic circuits which have been recently proposed, the various abstract levels of designing adders i.e design using transistors and majority gates and the emerging nanotechnologies such as Quantum Dot Cellular Automata, Nanomagnetic Logic, Spin-Wave Device, where basic logic gate is a majority gate.
Various recent works have been done in the area of approximate computing leveraging the inherent error resilience of applications at various levels of design hierarchy . A new full adder design is proposed by Lin et al. (2007) which used very few transistors per bit i.e ten transistor per bit. This proposed design gives lower operating voltage, higher computing speed and lower energy operation when comparing with a low gate-count full adder design using pass transistor logic. A reconfigurable approximate carry look-ahead adder (RAP-CLA) which is fast as well as energy-efficient is proposed by Kyaw et al (2010). Here the conventional Carry-lookahead Adder (CLA) is modified to achieve more area and power efficient design than state-of-theart reconfigurable carry-lookahead adder. There are many types of approximate circuits, including those constructed by XOR/XNOR based gates which were proposed by Yang et al. (2013) and others as mentioned by Han & Orshansky, (2013) . The adders designed using QCA to reduce area complexity as well as power consumption are described in Padmavathy and Govindharajan (2017) , where four approximate adders were designed to compare the performance. The another approach to design the approximate adders is using nanomagnetic logic which again concentrated over reducing area complexity. It is a new paradigm to design approximate circuits for emerging nanotechnology devices (Gupta et al., 2013) .
For approximate implementation of adders, two types of adders are considered i.e multiple bit adders and single bit adders. The multiple adders are divided into two parts i.e lower and upper bits. The lower bits (less significant bits) are considered as approximate parts while upper bits (more significant bits) are considered as accurate. To implement the lower part, single bit adder is modified and thus it becomes inexact function of addition (Han & Orshansky, (2013) . This paper reviewed the single bit adders with different techniques.
Researchers have done lots of work for designing energy efficient designs to be incorporated into integrated circuits for reducing power consumption. As the technology scales down and Moore’s law shows its economic and technical limits after four decades of prosperity, approximate computing can be implemented with different abstraction layers starting from technology, hardware design, to algorithm or software level. This review is focused on energy efficient designs, the primitive techniques using Complementary Metal Oxide Semiconductor (CMOS) and emerging technologies which can overcome the limitations of Moore’s law.
The simple design approach for designing of Mirror Adders (MA) is implemented and the procedure is explained by Gupta et al. (2013) . The removal of few transistors connected in series results into faster charging/ discharging of node capacitances. The removal of transistors reduces the complexity, ultimately reduces switched capacitance i.e αC in the dynamic power expression.
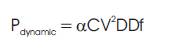
where α is the average number of switching transitions per unit time and C is load capacitance which will charged/ discharged. Reduction in switched capacitances will directly result in low power dissipation. This approach can achieve area reduction. Further section will describe the implementation of conventional MA followed by approximate MA.
A new technology based on QCA cells offers advanced computation to design functionality at nanometer range and to exploit the quantum effects when dealing with small size. This technology might improve the conventional design technology (CMOS). The QCA has more advanced feature that it has high packing density because of the small size of the dots. In this new paradigm, the basic logic element is not a current switch, but depends on a small array of quantum dots, and the logic state is determined by the position of individual electrons within a quantum dot cell.
It is a new topology of designing the gates where nano scale magnetic cells are the base of Nanomagnetic logic (NML). There are two logics i.e logic 0 and logic 1, for each cell. The logic is determined by the magnetic polarization of each cell. Polarized up is considered as logic 1 and polarized down is considered as logic 0. The interconnection i.e wires can be generated by cascading multiple cells. Two different arrangements can be done for the placement of cells
The main gates in NML are the majority voter and the inverter. Inverters are created by simply placing cells side by side as their magnetic properties will cause the signal to invert. The majority voter is also known as three-input majority gate (Labrado et al., 2017).
Gupta et al. (2013) proposed an approximate mirror adder design from conventional MA adders, but the approach achieved less transistor count and thus reduction in area. This approach was employed to remove selected transistors as no complementary CMOS logic was used. Here four approximate adders were proposed and all the adders were compared with the conventional one. The approximate outputs of adder i.e sum and carry, are compared with accurate outputs.
The comparison of accurate adder and approximate outputs are given in Table 1.
The another approach to design the approximate adders is proposed by Yang et al (2013). The XOR/XNOR based adder (AXA) designs are proposed to reduce area complexity and power consumption. The accurate adder is based on XNOR gates and less number of transistors are used i.e 10 transistors are sufficient to design a full adder. Based on this adder design, three approximate adders are proposed (Yang et al., 2013) .
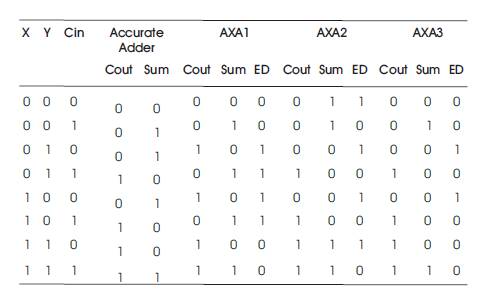
Table 2. (ED) OF AXAs Truth Table and Error Distance (Yang et al., 2013)
The QCA based designs are proposed by Padmavathy and Govindharajan (2017). One bit QCA adder is proposed along with four different approximation approaches implemented. The difference in the approximation of four designed is to give different types of input to calculate sum and carry. The proposed designs used one majority gate for sum and one majority gate for cout along with different combinations of inputs. All the proposed designs are shown by Padmavathy and Govindharajan (2017) . The equation of sum and carry for different designs are summarized here.
Hence the proposed one bit full adder is implemented using three majority gates and two inverter. Whereas all the approximated adders were implemented using one majority gate and inverter. Table 3 shows the error distance calculated for all approximate adders with respect to accurate adder. Thus, A1, A2 shows minimum error distance than A3 and A4. A4 reduces majority gate to one but shows higher error distance. Hence A1 and A2 would be more preferable designs (Akbari et al., 2016; Kulkarni et al., 2011; Schlachter et al., 2017; Verma et al., 2008; Vinitha et al., 2017) .
Table 3. Truth Table and Error Distance (ED) of QCA Logic Adders (Padmavathy and Govindharajan, 2017)
The approximate designs achieved from the combination of approximate computing and nanotechnology are proposed by Labrado et al. (2017). The nanomagnetic logic based majority gates and inverters are basic cells to design the adder. The adder-subtractor (Addsub) are proposed using majority gates and inverter. The schematic is clearly described by Labrado et al. (2017). For the comparison sake, adder-subtractor designs are considered. The MED) is calculated here (Labrado et al., 2017) . Total Error Distance (TED) is also considered here. The Table 4 shows the truth table and ED of Addsubs.
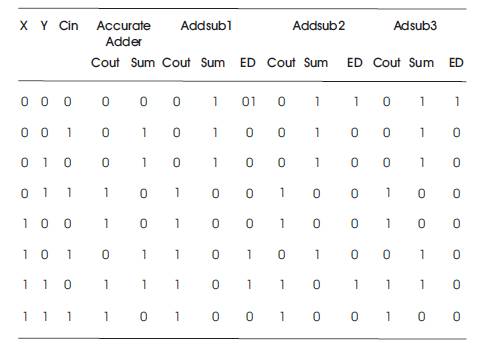
Table 4. Truth Table and Error Distance (ED) of Addsubs (Labrado et al., 2017)
To evaluate the accuracy of the circuit, some comparative metrics should be necessary. For that reason, it is important to evaluate approximate computing designs on their accuracy compared to completely correct designs. In this work, Error Distance (ED) has been used to evaluate the designs and are compared with correct designs. Error Distance (ED) is the absolute difference between two binary numbers a and b, where a is the erroneous number and b is the correct number. ED can be calculated by the following equation:
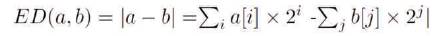
As an example, say a given input combination results in an output of 11 from a correct adder and 01 from an approximate adder. The ED would be 2 as that is its distance from the correct value. A correct circuit would have a MED of 0, as each input vector would result in an ED of 0. Therefore, it is desirable that the TED of a given approximate circuit be as minimum as possible.
The total error distance is presented for each approximate design, number of transistor and logic gates. In these designs, Error distance is used as a comparison metric for all the designs. Through the comparison parameters of the adders, accuracy can be obtained. In this work, four design topologies are presented i.e. transistor logicbased Mirror adders, XOR/XNOR based adders, QCA based adders and NML based adders have been analyzed and come up with their transistor count and ED.
Among the adders studied, the QCA based adders have one majority gate and inverter. NML logic based adders, specifically AddSub3, has less error distance obtained as 1. But it counts less ED on the expense of more number of majority gates. The approximate mirrror adder also shows less ED and but is implemented with many transistors. The XOR/XNOR based adders show more ED than mirror adders, but are implemented with less number of transistor count than mirror adders. The analysis of approximate adders are given in Table 5.
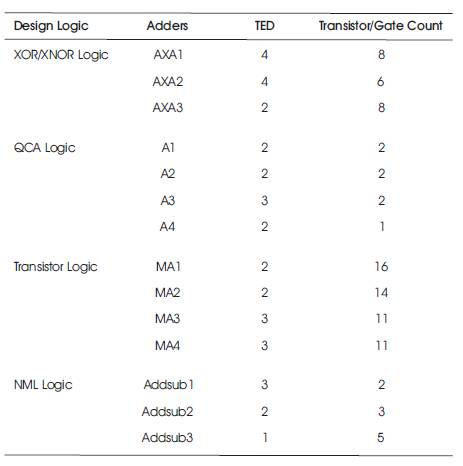
Table 5. Analysis of Approximate Adders
In this paper, recent progress on approximate computing is reviewed, with a focus on approximate circuit design, error metrics, and various design techniques. As an emerging paradigm, approximate computing shows great promise for implementing energy-efficient and error-tolerant systems. This paper explains about the approximate adder circuits and its design topologies. The total error distances for all the designs are listed in Table 5. As per the requirement of more accuracy and less number of designing cells, QCA based adders having least majority gate count confirms the expected circuit performance. Also, they achieve lower TED which shows that they are the most accurate designs among all other designs. This design topology has lowest power dissipation among all proposed adders.