The fundamental operations involved in any digital systems are addition and multiplication. Addition is an indispensable operation in any Digital, Analog, or Control system. Fast and accurate operation of the digital system depends on the performance of adders. The main function of an adder is to speed up the addition of partial products generated during the multiplication operation. Hence, improving the speed by the reduction in area is the main area of research in the VLSI system design. Over the last decade, many types of adder architectures were studied, such as carry ripple adders, carry skip adders, carry look ahead adders, parallel prefix tree adders, etc. In tree adders, carries are generated in parallel and fast computation is obtained at the expense of increased area and power. The main advantage of the design is that, the carry tree reduces the number of logic levels (N) by essentially generating the carries in parallel. Parallel prefix adders are preferable for high performance [11].

The parallel-prefix tree adders are more favorable in terms of speed due to the complexity O(log N) delay through the 2 carry path compared to that of other adders. The prominent parallel prefix tree adders are Kogge-Stone, and Brent- Kung, and Han-Carlson adders.

Parallel Prefix Adder (PPA) is very useful in today’s world of technology because of its implementation in Very Large Scale Integration (VLSI) chips. The VLSI chips rely heavily on fast and reliable arithmetic computation. These contributions can be provided by PPA. There are many types of PPA such as Brent Kung, Kogge Stone, Ladner Fisher [8], Hans Carlson and Knowles [9] . For the purpose of this research, only Brent Kung and Kogge Stone adders will be investigated.

An adder is a Digital Design Addition [7], which is one of the four elementary operations in mathematics, the others being subtraction, multiplication, and division. In digital systems, addition forms the most important operation. This is primarily because we can perform operations like subtraction, multiplication, and division using the addition operation. Hence, the design of a very fast, accurate and a lower power consumption adder directly results in the increased speed of the device for faster computational purpose as well as an improved life.

The basic complete form of addition can be implemented by the Half Adder and improvised by the Full Adder. The generated carry bit plays a very important role in the adder design. The speed of the adder is decided to a great extent by the carry propagation. To reduce the carry propagation delay, multiple adders are designed. Some of the most commonly used adders are Carry Look Ahead Adder, Carry Skip Adder, Carry Select Adder, Manchester Chain Adder and Parallel Prefix Adders.

While designing an adder, lot of constraints come into the picture, the trade-off between speed and size being the most important one. The most basic adder has a very small area and is very easy to implement. But the delay involved in obtaining the output is very huge. Hence, new designs came into picture. But in the current age, the power consumed by the device is also a very important constraint. Hence designing an adder, which is very close in meeting all these requirements is very important.

Compared to the ripple carry adders, parallel prefix adders are fast and more efficient for binary addition. Using simulation studies, the area, delay and speed performance of the various adder modules were obtained. It was observed that, Kogge Stone Prefix tree adder has better circuit characteristics in terms of speed compared to adders realized using other algorithms. The paper provides the objective of the paper in section 1 and section 2 contains a succinct explanation about the parallel prefix adders. Different parallel prefix adders are given in section 3 and simulation results are given in section 4 and finally the last section concludes the paper.

The main objective of this work is to implement a Parallel Prefix Adder based Kogge Stone adder which makes use of high speed arithmetic operation. Prefix adders are tree structure based and preferred to speed up the binary additions. The verilog source code writing is the most important part of this paper. There are a total of three verilog source codes for 16 bits for Brent-kung, Han Carlson and Kogge Stone adders. This work estimates the various parallel prefix adders performance in terms of speed, delay, area, and power consumption. The experimental results show that the performance of the Kogge Stone adder is faster and area efficient compared to the Brent -kung adder.

The Parallel Prefix Adder (PPA) is considered to be one of the fastest type of adder designs possible [3]. It is a commonly used adder type for high speed addition. It is flexible and well suited for VLSI implementation [10]. Until now, it is seen that when two numbers are added, we get a sum and a carry bit. Based on the Carry Look-Ahead Adder operation, one can categorize the addition operation in three different stages. They are,

• The first stage is the pre-processing stage, where we obtain the Group Generate and Group Propagate signals.
• The second stage is the carry generation stage, where we generate the carry using the Group Generate and Group Propagate signals.
• Third and final stage are where we obtain the sum bit .

3.1 A 16-Bit BK Adder

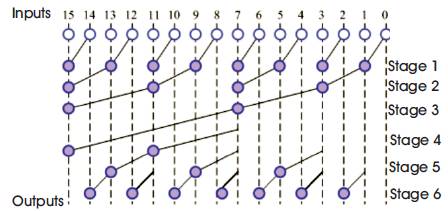
Brent-Kung adder is a very popular and widely used adder. It actually gives an excellent number of stages from input to all outputs, but with an asymmetric loading of Intermediate stages. It is one of the parallel prefix adders, where these adders are the ultimate class of adders that are based on the use of generate and propagate signals. In the case of Brent-Kung adders, along with the cost, the wiring complexity is also less. But the gate level depth of Brent- Kung adders is 0(log (n)), and so the speed is lower [6] . The 2 architecture of Brent-kung adder is shown in Figure 1.

Figure 1. BK Adder

The simulation and waveforms of a Brent-kung adder are shown in Figure 2. Let input bits be A and B. A = a₀.....a₁₅ ., and B = b₀ .......b₁₅ ., sum = s₀......s₁₅ and carry is generated.

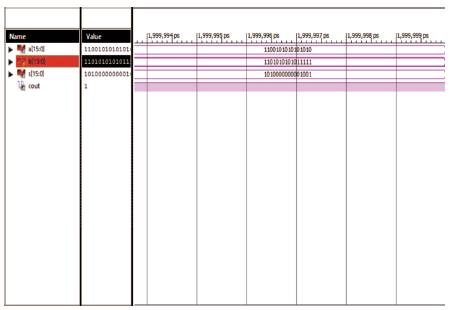
Figure 2. Waveforms of BK Adder

3.2 A 16-bit HC Adder

The Han-Carlson adder [1] is a blend of the Brent-Kung and Kogge-Stone adders. It uses one Brent-Kung stage at the beginning, followed by Kogge-Stone stages, terminating the other Brent-Kung stages to compute the odd numbered prefixes [4]. Comparing to the KS structure, it reduces the wiring and gates [5]. The architecture of Han Carlson adder is shown in Figure 3.

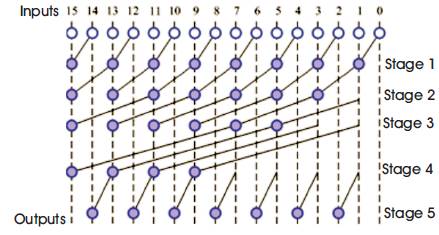
Figure 3. HC Adder

The simulation and waveforms of Han Carlson adder is shown in Figure 4. Let input bits be A and B. A = a₀ .....a₁₅ , and B = b₀ .......b₁₅ , sum = s₀ ......s₁₅ and the carry is generated.

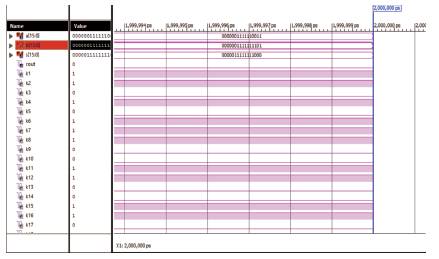
Figure 4. Waveforms of HC Adder

3.3 A 16-bit KS Adder

The Kogge-Stone adder is a parallel prefix form carry look ahead adder. The Kogge-Stone adder concept was developed by Peter. M.Kogge and Harold S.Stone, which they published in 1973 in a seminal paper titled, ‘A parallel Algorithm for the Efficient Solution of a General class of Recurrence Equations’ probably while listening to a Yes or King Crimson album, Kogge and Stone came up with the idea of parallel- prefix computation.

KS generates carry in O(log n) time and is widely considered as the fastest adder and used in the industry as high performance arithmetic circuits. In KSA, the carries are computed fast by computing them in parallel at the cost of increased area [2]. The area of KS adder is (n*log2n)-n+1, where n is the number of input bits [3]. KS adder has minimum fan-out so it becomes the fastest adder but it occupies a large area. The tree diagram of KS adder is shown in Figure 5.

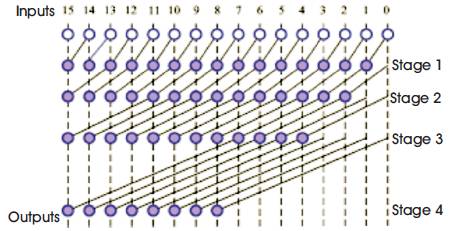
Figure 5. KS Adder

The simulation and waveforms of the Kogge Stone adder are shown in Figure 6. Let input bits be A and B. A = a₀ .....a₁₅ , and B = b₀ .......b₁₅, sum = s₀......s₁₅ and the carry is generated.

Figure 6. Waveforms of KS Adder

Various adders were designed in Verilog using Xilinx 14.5. The simulated adder delays obtained from the Xilinx ISE synthesis reports are shown in Figures 2, 4 and 6. The comparison of various adders for different parameters, delay, speed and power consumption is shown in Table 1. All the parallel prefix adders are 16-bit adders. The first stage is the preprocessing stage and the second stage is the carry generation stage, where we generate the carry using the Group Generate and Group Propagate signals. The third and final stages are where we obtain the sum bit. The resulting analysis shows that, Kogge Stone Adder shows better results than the Brent-kung Adder architectures in terms of delay and high speed. They also show better results when high speed is required Compared to Brent- Kung, the Han Carlson and Kogge Stone Adders power consumption is reduced and the area is also reduced in the Han Carlson and Kogge Stone Adders. It also shows that, non-speculative adders remain as the best choice, when the speed constraint is relaxed.

The primary objective of this paper is the performance comparison of various parallel prefix adders. In this paper, several adders were analyzed to identify the optimal adder modules that can be used for the realization of high speed or low power adder structures. The addition algorithms that were studied include three different types of prefix tree adders. Each kind of adders have different properties in terms of propagation delay, interconnect usage and power consumption. Figures 2, 4 and 6 contain the results obtained. Table 1 contains the comparison of Brent-Kung Adder, Han-Carlson Adder and Kogge Stone Adders. By the simulation results, it is known that all the adders are functionally verified and Kogge Stone Adder is more efficient than that of Brent kung and Han Carlson Adders. The Han-Carlson exhibited the best performance in terms of area, and power consumption. The speed is increased, while the delay is reduced compared to the Brent kung Adder. Therefore, the Kogge Stone adder exhibited best performance in terms of area and speed, while delay is reduced when compared to the Han Carlson and Brent- Kung adders.

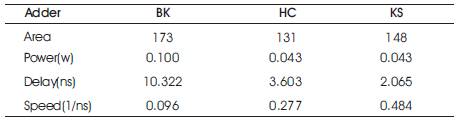
Table 1. Comparison of KS, HC, BK Adders

The authors are grateful to Mrs. M. Bharathi, Assistant Professor in the Department of Electronics and communication Engineering at SVEC, Tirupati, India, for her valuable inputs and advice. It was not just a piece of cake guidance but her suggestions were proved to be precious not only for this survey but also a great value for their careers.