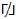 ’’ is used) = [
’’ is used) = [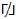 1].
1].The narrative in this discourse provides the third part of an epistemological rational for the novel discipline of “Trioinformatics”. This novel application of trioinformatic notation in mathematical form is the continuation of the Trioinformatics article that appeared in the March–May i- manager’s Journal on Circuits and Systems,“Trichotomous Charge States” [denoted by the acronym “TCS”] use “Neuroengineering Neuromathematics Notation” as the explicative expression of Trioinformatics in “Polyphase Electrical Systems” and electronic “Tri–State Buffers”. Trioinformatics Neuroengineering also has broad applications when used as an innovative way of explaining the transition from trichotomous logic (Osler, 2015) into trichotomous Triple–I (Osler, 2013d) research questions and associated instrumentation [first introduced in the i-manager’s Journal on Mathematics as a part of the Tri–Squared Test (Osler, 2012a)]. Trioinformatics is an in–depth way of symbolically illustrating the law of trichotomy and a mathematically–grounded rational technique for explaining the ternary properties of electronic circuitry (Osler, 2015). The use of Trioinformatics also adds value to investigative inquiry through the efficacy of digital instruments and tools via eduscientifically–engineered (Osler, 2013) research designs (Osler, 2015). Additional research into trioinformatics and its neuroengineered neuromathematical notation will further advance in–depth investigations into the tripartite aspects of digital instrumentation and digital / electronic circuitry.
“Trichotomous Charge States” [“Tri-Charge States” denoted by the acronym “TCS”] are a method of determining the overall efficacy of the trichotomous “three-states” found in natural phenomena. These states can be actively applied to the conceptualization of a tool or the application of a particular technology. TCS must always be clearly, precisely, and specifically defined to provide clarity of the concept under TCS methodology and protocols. The use of “Trichotomous Charge States” provides a clear vision into and indeed a more profound in–depth insight of the manifold infrastructure of the universe. Careful observations nature yield the existence of “Trichotomous Electrical” or “Tri–electrical”, i.e., “Trielectrical” charges (“Trielectrical” is a general term for the three natural states of “attraction” which is “magnetic”; “transmission” which is “electric”; and “no motion” which is “stasis”). Thus, the understanding of “Trichotomous Charge States” as a technique begins with the comprehension and general understanding of the general definition of a “charge” followed by its application in aforementioned “trifold trichotomous - charge states”.
A “Charge” by definition, is a basic property of matter that can be observed on a subatomic scale. Upon observation of an atom, one will not concentrate on the existence of the three trichotomous components, elements, or particles. The three trichotomous parts of an atom are, “the proton” which has a positive or electrical magnetic (or an “attraction”) charge; “the electron” which has a negative (or a “transmission”) charge; and lastly, “the neutron” which has “No Charge” that can be considered to be in a “null” state identified with “stasis” or “station” in terms of having a charge (and is a part of the subatomic nucleus along with the proton).
The above mentioned charges can be represented symbolically as,
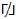 ’’ is used) = [
’’ is used) = [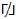 1].
1].The “antithetical symbol” was first introduced in the imanager’s March-May Journal on Circuits and Systems in an article entitled, “Trioinformatics: The Innovative and Novel Logic Notation that Defines, Explains, and Expresses the Rational Application of the Law of Trichotomy for Digital Instrumentation and Circuit Design”. According to this article, the “null state” as the “antithetical symbol” is specifically defined as follows: “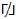 = The novel “closed antithetical” symbol is representative of a “non-aligned neutral” and is also a uniquely designed trichotomous logical symbol for “neither” or “neither is” that literally means “mathematical differential negation” form the first two “opposing values” or “opposite variables” that were presented in the initially given universal trichotomous cohesive rational statement for the mathematical notation of the logic of mathematical law of trichotomy”.
= The novel “closed antithetical” symbol is representative of a “non-aligned neutral” and is also a uniquely designed trichotomous logical symbol for “neither” or “neither is” that literally means “mathematical differential negation” form the first two “opposing values” or “opposite variables” that were presented in the initially given universal trichotomous cohesive rational statement for the mathematical notation of the logic of mathematical law of trichotomy”.
The overall objective of this paper is to provide further explanation for the existence of “Trichotomous Charge States” that were first mentioned in the March–May imanager’s Journal on Circuits and Systems. “Trichotomous Charge States” [denoted by the acronym “TCS”] are explained in detail through the use of “Neuroengineering Neuromathematics Notation” as the explicative expression of Trioinformatics in “Polyphase Electrical Systems” and electronic “Tri–State Buffers”. Further investigative research into TCS has shown that a charge state has its existence based on its application to some pre-existing form of matter. If there is no matter, then there is no TCS. As such, the charge must then be directly applied to the substance, material, or existing matter. This explains the purposeful use of a numerical identification of said matter as the integer “1” in TCS explicative “Trioinformatics” as the overriding “conceptual framework” (Ravitch & Riggan, 2011) of TCS. Furthermore, the use of the Trioinformatics mathematical operation adds a well-grounded neuroscientific (Research Network on Law and Neuro science, 2014), neuroengineering (Osler, 2015), and neuromathematics (Osler, 2015) foundation to TCS. Trioinformatics Neuroengineering also has broad applications when used as an innovative way of explaining the transition from trichotomous logic (Osler, 2015) into trichotomous Triple–I (Osler, 2013d) research questions and associated instrumentation [first introduced in the i-manager’s Journal on Mathematics as a part of the Tri–Squared Test (Osler, 2012a)]. These aforementioned foundational parameters add both breadth and depth to the conceptualization of TCS as an operational science that has direct applicability in terms of the identification and use of Trichotomous Charge States in terms of polyphase electrical systems.
The base or “Basic Trichotomous Charge States” by definition are defined and can be applied in research and the observation of natural phenomena in the following manner,
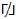 1 (the quantitative representation of a “neutral” TCS by definition is pronounced as “Null One”), in terms of a qualitative visual response to trichotomously organized items that are analyzed from observation of a respondent in the “Affective Learning Domain” [which is the sphere of attitudes, emotions, feelings, opinions, perceptions, and perspectives] the outcome identified as a “Nothing” or a “Zero”, Null or No Charge (symbolizing neither “Positive” or “Negative” i.e. and an “Empty” Charge). In Trichotomous State Charges, the state of “Neutral” does not mean a complete “zero” because the state of neutrality exists for the framework or source system, what does not exist is a charge which can be either positive or negative. This is similar to an atom which has protons (+), neutrons (0), and electrons (–). The neutron actually exists in the “subatomic epicenter” or “nucleus” of the atom much like the other two elements of the atom, it is simply neither positive (+), or negative (–). In terms of “polyphase trielectrical transference” this particular state is equal to zero impedance (Z) for buffering and resistance in an Trielectrical circuit. Table 1 follows and illustrates the “Computational Trioinformatic Table of Computational Trichotomous Charge States in Terms of Computational Information Transference”.
1 (the quantitative representation of a “neutral” TCS by definition is pronounced as “Null One”), in terms of a qualitative visual response to trichotomously organized items that are analyzed from observation of a respondent in the “Affective Learning Domain” [which is the sphere of attitudes, emotions, feelings, opinions, perceptions, and perspectives] the outcome identified as a “Nothing” or a “Zero”, Null or No Charge (symbolizing neither “Positive” or “Negative” i.e. and an “Empty” Charge). In Trichotomous State Charges, the state of “Neutral” does not mean a complete “zero” because the state of neutrality exists for the framework or source system, what does not exist is a charge which can be either positive or negative. This is similar to an atom which has protons (+), neutrons (0), and electrons (–). The neutron actually exists in the “subatomic epicenter” or “nucleus” of the atom much like the other two elements of the atom, it is simply neither positive (+), or negative (–). In terms of “polyphase trielectrical transference” this particular state is equal to zero impedance (Z) for buffering and resistance in an Trielectrical circuit. Table 1 follows and illustrates the “Computational Trioinformatic Table of Computational Trichotomous Charge States in Terms of Computational Information Transference”.
Table 1. Computational Trioinformatic Table of Computational Trichotomous Charge States in Terms of Computational Information Transference [CIT]
When combining Trichotomous Charge States, the operation under observation is actually collaboratively combining or mixing the two identified charge state properties. This procedure is collectively referred to as “Trichotomous Charge State Combinatorics” (“TCS Combinatorics” or simply “Trichotomous Combinatorics”). The Trichotomous Combinatorics operation is a systemic procedure that is very similar to the science of chemistry in which two elements are combined and yields a new outcome. In fact, if one observes the chemical phenomenon of combining acidic substances with base (or caustic) substances, it perfectly parallels the collaborative combination of the three Trichotomous Charge States.
Trichotomous Combinatorics uses the 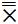 sign from “Proximal Positive Parallel Notation” first introduced by the author in 2013 i-manager’s Journal on Mathematics article entitled, “Proximal Positive Parallel Notation: A Novel Method of Expressing Mathematical Complements, Collaborations, and Combinations”. The
sign from “Proximal Positive Parallel Notation” first introduced by the author in 2013 i-manager’s Journal on Mathematics article entitled, “Proximal Positive Parallel Notation: A Novel Method of Expressing Mathematical Complements, Collaborations, and Combinations”. The 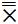 sign is called the “coextensive” and it indicates the one–to–one correspondence between the Proximal Positive Parallel Notation values. The coextensive sign is mathematically defined as the “Complementally Collaborative Combination” of the values that follow the Proximal Positive Parallel nomenclature (Osler, 2013c). In the case of Trichotomous Combinatorics, the Coextensive sign indicates the combination of two TSCs to yield a definitive outcome.
sign is called the “coextensive” and it indicates the one–to–one correspondence between the Proximal Positive Parallel Notation values. The coextensive sign is mathematically defined as the “Complementally Collaborative Combination” of the values that follow the Proximal Positive Parallel nomenclature (Osler, 2013c). In the case of Trichotomous Combinatorics, the Coextensive sign indicates the combination of two TSCs to yield a definitive outcome.
Only two charges are combined in a single Trichotomous Combinatorics expression. In terms of combinatorics operations in the combinations of two independent Trichotomous Charge States, the “antithetical neutral state” of “[Neutral = 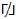 1]” always yields the strongest outcome. A state of neutral always “cancels out” and reduces other states to a neutral charge when combined with either a positive [+1] or a negative charge [–1]. This is much like the neutrality of acids and bases when combined in the field of chemistry. An example of the aforementioned cancellation as a Trichotomous Combinatorics expression is represented as follows:
1]” always yields the strongest outcome. A state of neutral always “cancels out” and reduces other states to a neutral charge when combined with either a positive [+1] or a negative charge [–1]. This is much like the neutrality of acids and bases when combined in the field of chemistry. An example of the aforementioned cancellation as a Trichotomous Combinatorics expression is represented as follows:
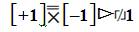
When completed this, particular Trichotomous Combinatorics operation is pronounced, “A TCS Positive when combined with a TCS Negative generates a TCS Neutral”. Table 2 displays in detail the varied Trichotomous Charge States in terms of the varied outcomes as a result of TSC Combinatorics. This expression uses the novel “Generare” (the Latin word for “Generate”) symbol indicated by a “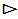 ”. Table 2 follows and displays the “Outcomes of Trichotomous Charge States Combinatorics for [+1] or [–1] or [
”. Table 2 follows and displays the “Outcomes of Trichotomous Charge States Combinatorics for [+1] or [–1] or [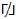 1] ”. Table 3 follows and displays TCS as ambitations.
1] ”. Table 3 follows and displays TCS as ambitations.
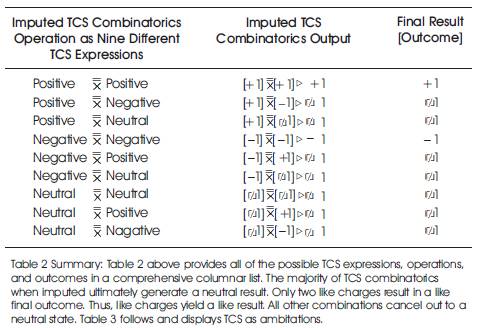
Table 2. Outcomes of Trichotomous Charge States Combinatorics for: [+1]; or[–1]; or [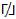 1]
1]

Table 3. Computational Trioinformatic Neuroengineering Neuromathematics Notation and Its Relation to the Table of Computational Trichotomous Charge States in Terms of [CIT]
A conceptual framework is often a graphical model grounded in a theory that serves as a descriptive and comprehensive analytical archetype that can be contextually applied to a variety of situations. It can be used to make specifically conceptualized distinctions based upon the organization of concretely defined ideas. A good conceptual framework is authentic and can be readily applied.
In the creation of design knowledge, Friedman provides definitions and parameters that can be applied to the rational function of a working conceptual framework. Friedman states about design knowledge that it has “features of something to be executed; an underlying scheme that governs functioning, developing or unfolding; a plan for carrying out or accomplishing something; the arrangement of elements or details in a product or work of art (Friedman, 2000).” Qualitative research pioneer in education, J. A. Maxwell says the following regarding the description of a conceptual framework, “the conceptual framework of your study-the system of concepts, assumptions, expectations, beliefs, and theories that supports and informs your research is a key part of your design (Miles & Huberman, 1994; Robson, 2011)”. Miles and Huberman (1994) defined a conceptual framework as a visual or written product, one that “explains, either graphically or in narrative form, the main things to be studied-the key factors, concepts, or variables-and the presumed relationships among them” (Miles & Huberman, 1994; Maxwell, 2012).
“Trioinformatics Neuroengineering Neuromathematics Notation” in and of itself is a conceptual framework exemplified in its “ambit” sign used to mathematically model the use of the mathematical law of trichotomy (Osler, 2012a) in the definition and illustration of the triune relationships found in nature. Thus, the trioinformatic neuroengineering “ambitation” (the mathematical parsimonious use of the ambit) of a concept, an idea, or a natural phenomenon all operate under a holistic trichotomous methodology. This methodology as a mathematical operation has at its base the rationale that all of the values under the ambit are trichotomous, related under a single whole. This means that all values that are contained within the ambit are interdependently related despite their intrinsic differences (which makes them uniquely trichotomous as they are two beginning values that are polar opposites followed immediately by a third value that is a neutral differential to the first two). As such, “ambitized” values are all holistically associated as they all represent different aspects that are correlated to a common whole. Thus the “neuromand” [a term that is a portmanteau of the two terms “neuroscience” and summand” literally meaning the “brain-based total of”] = 3 and the “index” = 1 that are invariantly unchanging above and below the ambit indicate a triune or “3 in 1” of all values contained within the ambit sign.
In terms of trioinformatic conceptual framework differentiation in terms of holistically neuroengineered natural phenomena that have natural trichotomous structures is evident in the following three ambitations as,
As ambit values, these subatomic natural phenomena are then ambitized (and subsequently illustrated to accurately define the ambitation) in the following expressions,

This expression is read and pronounced as follows, “The ambitation of proton (p) to electron (e) to neutron (n) from an index (i) that equals 1 and is inclusive of all 3 values”. The ambitation of the internal trichotomous trifold structures of the human body is represented and defined within the ambit as follows,

This expression is read and pronounced as follows, “The ambitation of the respiratory system (r) to the central nervous system (n) to the circulatory system (c) from an index (i) that equals 1 and is inclusive of all 3 values”. The ambitation of the trichotomous trifold structure of the three primary domains of learning is represented and defined as an ambitation that is written as follows,

This expression is read and pronounced as follows, “The ambitation of the cognitive learning domain (c) to the psychomotor learning domain (p) to the affective learning domain (a) from an index (i) that equals 1 and is inclusive of all 3 values”.
In terms of research and investigative inquiry, the discipline of “Trioinformatics” use of “Neuroengineering Neuromathematics Notation” is a novel way of using the parsimony of mathematics through brain-based learning (or cognitive neuroscience) to simplify the procedures used to transition from trichotomous logic to trichotomous instrumentation. Trichotomous instrumentation also known as the “Triple-I” or research “Inventive Investigative Instrument” (Osler 2012a & 2013d) is used in the Tri-Squared Test statistic (Osler, 2012a) to obtain qualitative data and information that will be transformed into quantitative data to validate and determine the initial efficacy of the Trioinformatic Trichotomous logically-based research questions and subsequent hypotheses. Much like the mathematical “Proximal Positive Parallel Notation” that was first introduced by the author in i-manager's October-December Journal on Mathematics, [Volume 2 (Number 4), pp. 21-31]. Proximal Positive Parallel Notation is a novel method of expressing mathematical complements, collaborations, and combinations (Osler, 2013c), likewise “Neuroengineering” uses many of the Proximal Positive Parallel Notation conventions to convey the transition from Trioinformatic Trichotomous logic to the Triple-I instrumentation and furthermore into the Tri-Squared test analysis.
Trichotomous Charges States can be found in many forms in natural phenomena. There is a group of “Sub-Trichotomous Charge States” within natural phenomena that can be described as a “Trichotomy Charge State within a Trichotomy Charge State” or a “Series of Sub-TCS”. This “Series of Sub-TCS” appears as “Trielectric” (or “te”), “Trimagnetic” (or “tm”) and “Tristatic”(or “ts”) and specifically defines, details, and describes the various forms of matter. These values can then be ambitized in the following expression,
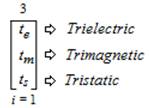
This expression is read and pronounced as follows, “The ambitation of the Trielectric Sub-Trichotomous Charge State of natural phenomena (te) to the Trimagnetic Sub- Trichotomous Charge State of natural phenomena (tm) to the Tristatic Sub-Trichotomous Charge State of natural phenomena (ts) from an index (i) that equals 1 and is s inclusive of all 3 values”. The properties of the trifold “Series of Sub-TCS forms of natural phenomena” are “Active”; “Reactive”; “Compact” and are further “Sub-Ambitized” as follows,
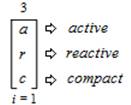
This expression is read and pronounced as follows, “The ambitation of active (a) to reactive (r) to the compact (c) from an index (i) that equals 1 and is inclusive of all 3 values”.
Trielectric are an “Active” (“Dynamic” and “Causational”) TCS and consist of a natural series of Trichotomous Charge States that can take any of the following Trichotomous forms: “Light” (i.e., the state of “radiance”, which has its own threefold within sub–trichotomous states that are: “photon”; “wave” and “radiation”) as ambit value (l);“Flame” (i.e., the state of “oxidation”) as ambit value (f); and “Electricity” (which has its own threefold within sub–trichotomous states that are: “arc”; “ball”; and “static”) as ambit value (e). As ambit values, these natural phenomena forms can then be ambitized in the following expression,
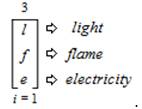
This expression is read and pronounced as follows, “The ambitation of the Trielectric Sub–Trichotomous Charge State of natural phenomena in the form = “Light” as value (l) to the Trielectric Sub-Trichotomous Charge State of natural phenomena in the form = “Flame” as value (f) to the Trielectric Sub-Trichotomous Charge State of natural phenomena in the form = “Electricity”as value (e) from an index (i) that equals 1 and is inclusive of all 3 values”. As a result of the “Light” value threefold within sub-trichotomous states that are formulated as: “photon” as value (p); “wave” as value (w); and “radiation” as value (r). The ambitation of the values is presented as,

This expression is read and pronounced as follows, “The ambitation of the Trielectric Sub-Trichotomous Charge State of natural phenomena in the form = “Light” as value (l) to the Trielectric Sub-Trichotomous Charge State of natural phenomena in the form = “Flame” as value (f) to the Trielectric Sub-Trichotomous Charge State of natural phenomena in the form = “Electricity” as value (e) from an index (i) that equals 1 and is inclusive of all 3 values”. As a result of the “Electricity” value threefold within subtrichotomous states that are formulated as: “arc” as value (a); “ball” as value (b); and “static” as value (s). The ambitation of the values is presented as,

Trimagnetic are a “Reactive” (“Malleable” and “Absorbable”) TCS and consist of a natural series of Trichotomous Charge States that can take any of the following Trichotomous forms: “Air”, “Water” and “Plasma”. As ambit values, these natural phenomena forms can then be ambitized in the following expression,
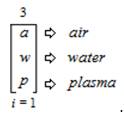
This expression is read and pronounced as follows, “The ambitation of the Trimagnetic Sub-Trichotomous Charge State of natural phenomena in the form = “Air” as value (a) to the Trimagnetic Sub-Trichotomous Charge State of natural phenomena in the form = “Water” as value (w) to the Trimagnetic Sub-Trichotomous Charge State of natural phenomena in the form = “Plasma” as value (p) from an index (i) that equals 1 and is inclusive of all 3 values”.
Tristatic are a “Compact” (“Solid” and “Dense”) TCS and consist of a natural series of Trichotomous Charge States that can take any of the following Trichotomous forms: “Dust”, “Earth” (which has its own threefold within sub–trichotomous states that are: “Gravity”, “Pressure” and “Mass”); and “Crystalline” (which has its own threefold within sub–trichotomous states that are: “Shape”, “Volume” and “Structure”). The “Structure” (has its own threefold within sub–trichotomous states that are : “Crystal”, “Metal” and “Mineral”). As ambit values, these natural phenomena forms can then be ambitized in the following expression,
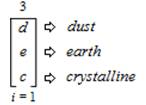
This expression is read and pronounced as follows, “The ambitation of the Tristatic Sub-Trichotomous Charge State of natural phenomena in the form = “Dust” as value (d) to the Tristatic Sub-Trichotomous Charge State of natural phenomena in the form = “Earth” as value (e) to the Tristatic Sub-Trichotomous Charge State of natural phenomena in the form = “Crystalline” as value (c) from an index (i) that equals 1 and is inclusive of all 3 values”. As a result of the “Earth” value threefold within sub-trichotomous states that are formulated as: “gravity”as value (g); “pressure” as value (p); and “mass”as value (m). The ambitation of the values is presented as,
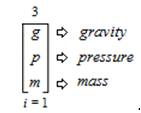
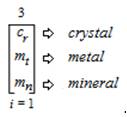
This expression is read and pronounced as follows, “The ambitation of the Tristatic Sub-Trichotomous Charge State of natural phenomena in the form = “Gravity” as value (g) to the Tristatic Sub-Trichotomous Charge State of natural phenomena in the form = “Pressure” as value (p) to the Tristatic Sub-Trichotomous Charge State of natural phenomena in the form = “Mass” as value (m) from an index (i) that equals 1 and is inclusive of all 3 values”. As a result of the “Structure” value threefold within subtrichotomous states that are formulated as: “crystal” as value (cr); “metal” as value (mt); and “mineral” as value (mn). The ambitation of the values is presented as,
The process of trioinformatic ambitation can also be applied to the scientific field of astronomy. Astronomical ambitations in terms of natural phenomena can be first applied in the form of three primary celestial bodies that are an active of earthly cycles of life that are readily identified and defined as,
The ambitation of the values is presented as,
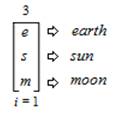
This expression is read and pronounced as follows, “The ambitation of the earth (e) to the sun (s) to the moon (m) from an index (i) that equals 1 and is inclusive of all 3 values”. As a result of the “Earth” value threefold within sub–trichotomous states that are formulated as: “air” as value (a); “land” as value (l); and “ocean” as value (o), an ambitation of the values is presented as,
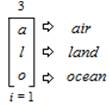
This expression is read and pronounced as follows, “The ambitation of air (a) to land (l) to ocean (o) from an index (i) that equals 1 and is inclusive of all 3 values”. As a result of the “Sun” value threefold within sub-trichotomous states that are formulated as: “light” as value (l); “spot” as value (s); and “flare” as value (f), an ambitation of the values is presented as,
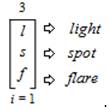
This expression is read and pronounced as follows, “The ambitation of light (l) to spot (s) to the flare (f) from an index (i) that equals 1 and is inclusive of all 3 values”. As a result of the “Moon” value threefold within sub-trichotomous states that are formulated as: “orbit” as value (o); “rotation” as value (r); and “pull” as value (p), an ambitation of the values is presented as,
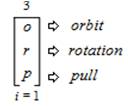
This expression is read and pronounced as follows, “The ambitation of orbit (o) to rotation (r) to pull (p) from an index (i) that equals 1 and is inclusive of all 3 values”.
The “Trichotomous Charges States Ambitation” as a trielectrical mathematical operation has multiple trichotomous parameters that are parallel to the electrical functions of different components that are an integral part of an electric grid. In terms of the aforementioned trielectrical components, the “Trioinformatics Neuroengineering Neuromathematic Notation Ambit” is a trifold operation that exemplifies the three different electrical components in its explicative use in the following manner,
An ambitation of these values is presented as,
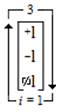
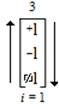
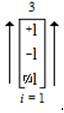
These three examples of the trielectric use of the ambit are further expounded in the next two sections that explain its use in “Trielectric Polyphase Electrical Structures” and “Trielectric Tri-State Buffer Structures”.
Just as Trichotomous Charges States can be found in many forms in natural phenomena, they can also be used to represent “Trielectric Polyphase Electrical Structures”. The electrical power system normally operates in a balanced three-phase sinusoidal steady-state mode. However, there are certain situations that can cause unbalanced operations. The most severe of these would be a fault or short circuit. Examples may include a tree in contact with a conductor, a lightning strike, or downed power line (Marx & Bender, 2013). In 1918, Dr. C. L. Fortescue wrote a paper entitled “Method of Symmetrical Coordinates Applied to the Solution of Polyphase Networks”, where he described how arbitrary unbalanced 3-phase voltages (or currents) could be transformed into 3 sets of balanced 3-phase components. He called these components “symmetrical components.” In the paper it is shown that, the unbalanced problems can be solved by the resolution of the currents and voltages into certain symmetrical relations. By the method of symmetrical coordinates, a set of unbalanced voltages (or currents) may be resolved into systems of balanced voltages (or currents) equal in number to the number of phases involved. The symmetrical component method reduces the complexity in solving for electrical quantities during power system disturbances (Marx & Bender, 2013). Figure 1 is an illustration of the three-phases of polyphase systems from the paper, “An Introduction to Symmetrical Components, System Modeling and Fault Calculation” written by Stephen Marx and Dean Bender for the Bonneville Power Administration presented at Washington State University at the 30th Annual HANDS-ON Relay School during March 11–15, 2013 in the original vector format (illustrating both magnitude and direction of polyphase systems).

Figure 1. Polyphase Electrical System Outcomes
As a Trielectric structure, the aforementioned “Polyphase Electrical System Outcomes” which are a TCS and consist of a natural series of Trichotomous Charge States have the following vectorization trichotomous forms: “Positive Sequence” (which has its own threefold within subtrichotomous states that are: “Positive Vector One” as ambit value [Va1]; “Positive Vector Two” as ambit value [Vb1]; and “Positive Vector Three” as ambit value [Vc1]); “Negative Sequence” (which has its own threefold within subtrichotomous states that are: “Negative Vector One” as ambit value [Va2]; “Negative Vector Two” as ambit value [Vb2]; and “Negative Vector Three” as ambit value [Vc2]); “Zero Sequence” (which has its own threefold within sub–trichotomous states that are: “Zero Vector One” as ambit value [Va0]; “Zero Vector Two” as ambit value [Vb0]; and “Zero Vector Three” as ambit value [Vc0]);. As ambit values, these trielectrical forms can then be ambitized in the following expressions,

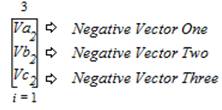

Trichotomous Charges States can represent “Trielectric Tri–State Buffer Structures” just as it also can represent “Trielectric Polyphase Electrical Structures”. A “Tri–State Buffer” is an electronic circuit that is for all intents and purposes similar to “a standard buffer” (which is an electronic circuit that has only a “single input” and a “single output” that passes its input, “unchanged”, directly to its output). Thus, a true “Tri–State Buffer” adds an additional “enable” input that controls whether the primary input is passed to its “output” (as “True” [or “Yes”] = +1) or “not” (as Hi–Z (Impedance) [that is “Resistance”] = 0). If the “enable” input signal is “true” [or equal to +1], the Tri–State buffer performs like a standard buffer (which is [as stated earlier] equal to single input and a single output that passes its input, unchanged, to its output). If the “enable” input signal is “false” (as “False” [or “No”] = –1), the Tri–State buffer passes a “high impedance” (or a “Hi–Z”) signal, which effectively disconnects its output from the circuit (as Hi–Z (or “Electrical Flow Impedance”) [that is, considered electrical power “Resistance”] = 0).
The term “Tri–State” is owned and copyrighted by National Semiconductor Corporation (NSC) as “TRI-STATE®” and is a registered trademark (National Semiconductor Corporation, 1998). NSC does allow other manufacturers to use the Tri–State name in their products. For example, in the Texas Instruments document, “54ACTQ16373 16-Bit Transparent Latch with TRI-STATE Outputs” describes in detail the operational parameters of a Tri–State Buffer on 16 “noninverting latches” that are a part of the “ACTQ 16373” 16 bit integrated circuit that utilized NSC Quiet Series technology to guarantee quiet output switching and improved dynamic threshold performance (Texas Instruments, 1998). Accordingly, Tri-State Buffers can be summarized in the Trielectric format via “Trioinformatic Neuroengineering as an ambitized expression [see ambit operation equation 24)] that details the operation of the buffer as both a digital switch and as a method of transferring power as a Trielectrical conduit (thereby differing slightly from a TCS in its output as “0” or “high impedance” rather than the antithetical "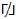 1"for the neutral state in terms of non-transferrable power through the given circuit). Table 4 illustrates “The Truth Table for a Tri-State Buffer”.
1"for the neutral state in terms of non-transferrable power through the given circuit). Table 4 illustrates “The Truth Table for a Tri-State Buffer”.

Table 4. The Truth Table for a Tri–State Buffer
Figure 2 illustrates the functional aspects of a Tri–State Buffer in a diagram that is equivalent to an electrical switch. As a Trielectrical technology, the structure of the aforementioned “Tri–State Buffer” has the following vectorization as an ambitized trichotomous operational form that is holistically illustrating the possible outcomes from Table 4. The ambitation that follows, illustrate the Tri–State Buffer outcomes in a cumulative and amassed whole.
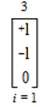
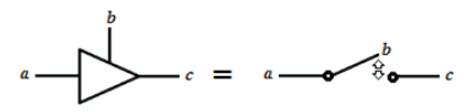
Figure 2. A Tri–State Buffer Diagram as Equivalent to a Digital Electronic Switch
This is equal to the initial TCS ambitation values “a”, “b”, and “c” in a base ambit expression which are most accurately detailed as follows,
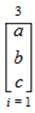
Trioinformatics: “Neuroengineering Neuromathematics Notation” has the following symbol called the “Ambit” sign meaning, “a neuroscientific neuroengineered neuromathematical circuit”. The use of the ambit symbol is referred to as the mathematical operation of “ambitation”. Ambitation is defined as the application of the mathematical “Law of Trichotomy” as a trichotomous sphere of extent and operation bounded within a specified mode, mechanism, and/or model with specifically defined and detailed purpose, range, and scope”. The neuroengineering notation ambit signification is written as follows,
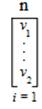
The expression (equation 21) is read and pronounced as follows, “The ambitation of v1 to v2 from I equals 1 inclusive of all n”, where, the Trioinformatics “Neuroengineering Neuromathematics Notation” is composed of the following elements,

“The Ambit Symbol” as displayed in (27) is an emblematic representation of the trichotomous mathematical operation of “ambitation” which literally means, “The total neuroengineered circumference, neuromathematical circuit, and neuroscientific trichotomous sphere that is a holistic operation, influence, range, and scope.
 =“The Continuous Connection to Corresponding Sub-Sequential Variables”, this symbolizes the trifold dual nature of the neuro engineering neuro mathematical ambit notation, as it can have two values directly symbolizing the nature of the variables of the Tri–Squared Test 3 × 3 Standard Table or it can symbolize as values or variables [“a”, “b”, and “c”] symbolizing the three initial trichotomous research questions that are presented in the Triple-I research instrument.
=“The Continuous Connection to Corresponding Sub-Sequential Variables”, this symbolizes the trifold dual nature of the neuro engineering neuro mathematical ambit notation, as it can have two values directly symbolizing the nature of the variables of the Tri–Squared Test 3 × 3 Standard Table or it can symbolize as values or variables [“a”, “b”, and “c”] symbolizing the three initial trichotomous research questions that are presented in the Triple-I research instrument.Note: The expression for (equation 1) literally means, “The ambit of value one as determined by value two with an index of 1 and a neuromand of 3”. It is also important to note that, when there are not three trichotomous values contained within the ambit, where the dual values are at the high and low ends of the ambit is indicative of the highest value determined by lowest value according to a specified criterion (for example an “x” and “y” placement of values representing Cartesian Coordinates, where “x” merits its overall outcome based upon “y”).
“Trioinformatics Neuroengineering Neuromathematics Notation” has its foundations in the mathematical research the author has conducted that led to the creation of “Proximal Positive Parallel Notation”. Historically the “Proximal Positive Parallel Notation” is property and an abstraction drawn out of the “Total Transitive Tandem of Visualus” first introduced in the book Visualus (Osler, 2010) written by the author in 2010. The “Proximal Positive Parallel Notation” nomenclature follows the aforementioned mathematical conventions and is of the following form,

or
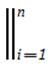
This particular method of mathematical writing and transforming the traditional mathematical parallel sign or symbol of “||” into the form seen in (equation 24) is called “Proximal Pairing” (Osler, 2013c). The “Proximal Pairing” in terms of coordinates relate to the positive values in the first quadrant of the Cartesian Coordinate graph (values that are integers and are [positive, positive] in regards to the Cartesian Coordinate abscissa [x] and ordinate [y]). It also symbolizes the proximal, parallel, positive, collaborative, and connectedness of the Trioinformatic trichotomous logic of the initial trifold research questions, Triple-I instrument, Tri-Squared Test Trichotomous Categorical Variables: [TCV: as variables “a1”, “a2”, and “a3”], Tri- Squared Test Trichotomous Outcome Variables: [TOV: as variables “b1”, “b2”, and “b3”], and the Tri-Squared Test 3 × 3 Standard Table.
An ideal example of the use of neuroengineering neuromathematics notation can be evidenced in its use to explain and define the systemic procedures used to move from trioinformatic trichotomous logical statements to the Tri–Squared Test 3 × 3 Standard Table. The actual sequential procedures used to move from the trichotomous research questions to the Standard 3 × 3 Table are as follows,
The neuroengineering neuromathematical notation for this research progression is written as follows,
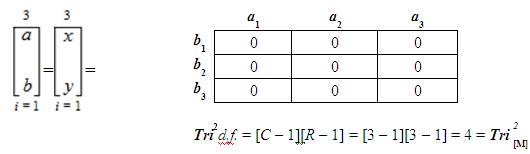
where equation (29) is defined as follows,
Note: The expression for (equation 2) is literally stated as, “The ambit of a as determined by b with an index of 1 and a neuromand of 3 is equal to the ambit of x as determined by y with and index of 1 and a neuromand of 3 which in turn is also equal to the Standard Tri–Squared Test 3 × 3 Table”.
It is important to note that equation (2) can also be represented by the explicative neuroengineered neuromathematical notation.
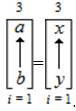
where equation (30) is defined as follows,
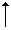 = Symbolizes that the TOV is determining the outcomes directly drawn from and pertaining to the TCV (in terms of variables and cartesian coordinates). Thus, the expression for (equation 3) is literally stated as, “The ambit of a as determined via outcomes directly drawn from b with an index of 1 and a neuromand of 3 is equal to the ambit of x as determined via outcomes directly drawn from y with and index of 1 and a neuromand of 3”.
= Symbolizes that the TOV is determining the outcomes directly drawn from and pertaining to the TCV (in terms of variables and cartesian coordinates). Thus, the expression for (equation 3) is literally stated as, “The ambit of a as determined via outcomes directly drawn from b with an index of 1 and a neuromand of 3 is equal to the ambit of x as determined via outcomes directly drawn from y with and index of 1 and a neuromand of 3”.Additionally, the research questions that formulated the TCV and the subsequent TOV are written in terms of the neuroengineered neuromathematical notation as,
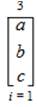
Note: The expression for (equation 4) is literally stated as, “The ambit of a followed by b and c with an index of 1 and a neuromand of 3”. Figure 3 follows and displays invariant structure of the Tri-Squared Test Inventive Investigative Instrument.
Figure 4 is an illustration by the author adapted, reillustrated, and re-drafted after observing the illustration of the human brain in the work of Feidakis, M., & Daradoumis, T. (2013). The original illustration appears in “A Framework for Designing Computer Supported Learning Systems with Sensibility”. It can be found in the, “International Journal of e-Collaboration” (IJeC), 9(1), pp. 57-70 [Image from doi:10.4018/jec.2013010105].
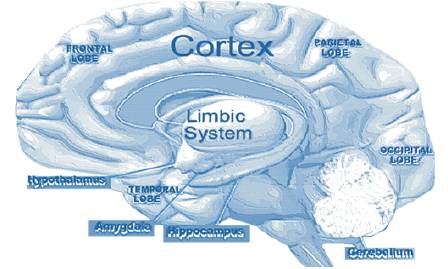
Figure 4. A Detailed Illustration of the Multiple Neuromathematic Triune Structures of the Human Brain [In Deference to Term Neurolaw in Section 13]
The “Multiple Trifold/Tripartite/Triplex Structure of the Human Brain” given in Figure 4 is a model that illustrates the neuromathematic trichotomous neuroscientific organizations of the human brain in terms of “Tri-Biological” structures that are identified as, Figure 4[a.] “Trilimbic” systemic structure as: Hypothalamus/Amygdala/ Hippocampus; Figure 4[b.] “Trilobic” structural groupings as: Frontal/Parietal/Occipital; Frontal/Temporal/Parietal; Frontal/Temporal/Occipital; Parietal/Temporal/Occipital etc.; and Figure 4[c.] “Tricerebral” systemic structure as: Cortex/Limbic/Cerebellum that lend to leadership include: The “neocortex” portion of the human brain that has the cluster of myelinated sheaths of neuronal axons as dynamically active brain structures involved in higher cognitive functions that trichotomously and holistically includes. Figure 4(1.) Advanced cognitive thought processes; Figure 4(2.) Systemic and sequential functions that are involved in detailed planning; and Figure 4(3.) Active procedures are involved in the process of dynamic mental modeling and detailed sensory simulations.
The internal “limbic brain” refers to the portion of the brain comprised of the basal ganglia (also more commonly referred to as the “basal nuclei”) that comprise the multiple subcortical internal human brain nuclei and its internal structures that are neuromathematically and trichotomously in charge of advanced emotional intelligence represented by Figure 4[d.] Advanced engaging teamwork through social interactions that can be expressed as parental nurturing and group-think mechanisms that are expressed as compassionate behavior; Figure 4[e.] Advanced interactive and empowering neurocordial metacognition typically expressed as external and mutual reciprocity; and Figure 4[f.] Advanced perceptive and perspective insight that creates internal interpretation of rapport expressed as external empathy and connectivity with others. The “cerebral cortex” portion of the human brain that has the cluster of cortial columnal nicrocircuits as the active and interspersed brain structures involved in cognitive holistic neuromathematic trichotomous functions that are not limited to but primarily include,
The following definitions are supportive of “Trioinformatics Neuroengineering”,
The conceptualization of novel arenas of discovery through innovation and experimentation often yields new frames of reference used to define natural phenomena. Mathematical logic is a subfield of mathematics exploring the applications of formal logic to mathematics (Osler, 2015). It bears close connections to metamathematics, the foundations of mathematics, and theoretical computer science (as stated by Boolos, Burgess & Jeffrey (2002), Enderton & Enderton (2001), Mendelson (2009), and Shoenfield & Monk (2001)). According to Ferreirós, mathematical logic emerged in the mid-19th century as a subfield of mathematics independent of the traditional study of logic (Ferreirós, 2001, p. 443). Mathematical logic is primarily a formal system that can be referred to as a “deductive system”. A deductive system (also called a deductive apparatus of a formal system) consists of the axioms (or axiom schemata) and rules of inference that can be used to derive the theorems of the system (Hunter,1973). Trichotomous logic as the core foundational infrastructure of the discipline of trioinformatics is a deductive system that provides the rationale for trichotomous research, inquiry, and logical trichotomous reasoning. In terms of the mathematical law of trichotomy, this can be expressed using “trichotomous logic” that is contained within the new discipline of “Trioinformatics” (Osler, 2015). Trioinformatics is the scientific discipline that specifically addresses and studies trichotomous logic and trichotomous logical data structures for the purposes of research and problem–solving. Trichotomous logic can parsimoniously be expressed as: Tri[Logic] . The logic of trichotomy has its application in the trichotomous outcomes (“a, b, or c”) that are derived to express some unique or “universal” concept or idea. The universal concept or idea (for the specific purposes of trichotomous logic) is referred to as the “Universal Trichotomous Statement” (a “Cohesive Rational Statement” also identified by the acronym “U-Tri[S]” = Tri [Logic] for the purposes of parsimony). The Universal Trichotomous Cohesive Rational Statement has the trichotomous logic expression of: Tri[a;b; or c] and the variables “a, b, and c”. The trichotomous logic expression is equal to the UTCRS expression as they are both the same form of the same idea and only one further defines and refines the idea in terms of implicit and explicit variation. Mathematically, this is conveyed in the subsequent trioinformatic trichotomous logic model.
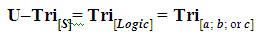
The variables “a, b, and c” in trioinformatic trichotomous logic are enclosed within the enlarged brackets “[]” (though different in their respective positions, the three are all holistically a part of the same idea or concept; regarding the “Universal Trichotomous Statement” (the Cohesive Rational Statement) or “U-Tri[s]” which can also be expressed as, “Tri[a; b; or c] ”) (Osler, 2015). Thus, the brackets indicate that the variables (a, b, and c) are uniformly and directly related through a singular given statement, inquiry, and/or term for the specific purposes of determining an individual outcome (that is trichotomously “a; b; or c”). The logical mathematical notation for the decision–making process regarding the Universal Trichotomous Cohesive Rational Statement is of the following novel form.
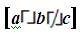
The aforementioned statement is pronounced as follows, “Variable a opposed by Variable b and neither is Variable c”. Each of the terms represented in the logical notation of the mathematical law of trichotomy is defined as follows,
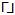 = The novel “antithetical” symbol is representative of “opposition” to the initially presented variable and is a uniquely designed trichotomous logical symbol for “opposed”, “opposed by” or “opposite” that literally means “mathematical opposites”, “mathematical opposing values” or “mathematically opposite variables” in the given universal trichotomous cohesive rational statement for the mathematical notation of the logic of the mathematical law of trichotomy.
= The novel “antithetical” symbol is representative of “opposition” to the initially presented variable and is a uniquely designed trichotomous logical symbol for “opposed”, “opposed by” or “opposite” that literally means “mathematical opposites”, “mathematical opposing values” or “mathematically opposite variables” in the given universal trichotomous cohesive rational statement for the mathematical notation of the logic of the mathematical law of trichotomy.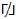 = The novel “closed antithetical” symbol is RESEARCH PAPERS representative of a “non-aligned neutral” and is also a uniquely designed trichotomous logical symbol for “neither ” or “neither is” that literally means “mathematical differential negation” form the first two “opposing values” or “opposite variables” that were presented in the initially given universal trichotomous cohesive rational statement for the mathematical notation of the logic of the mathematical law of trichotomy (Osler, 2015).
= The novel “closed antithetical” symbol is RESEARCH PAPERS representative of a “non-aligned neutral” and is also a uniquely designed trichotomous logical symbol for “neither ” or “neither is” that literally means “mathematical differential negation” form the first two “opposing values” or “opposite variables” that were presented in the initially given universal trichotomous cohesive rational statement for the mathematical notation of the logic of the mathematical law of trichotomy (Osler, 2015).In terms of mathematics, Apostol in his book on calculus defined “The Law of Tricohotomy” as: Every real number is negative, 0, or positive. The law is sometimes stated as “For arbitrary real numbers “a” and “b”, exactly one of the relations:
It is important to note that in mathematics, the law of trichotomy is most commonly the statement that for any (real) numbers x and y, exactly one of the following relations holds. Until the end of the 19th century, the law of trichotomy was tacitly assumed true without having been thoroughly examined (Singh, 1997). A proof was sought by Logicians and the law was indeed proved to be true. If applied to cardinal numbers, the law of trichotomy is equivalent to the axiom of choice (Osler, 2015). More generally, a binary relation R on X is trichotomous if for all x and y in X exactly one of xRy, yRx or x = y holds (Osler, 2013b). If such a relation is also transitive, it is a strict total order; this is a special case of a strict weak order. For example, in the ≠≠case of three elements the relation R is a strict total order given by:
While the relation “R” given by the cyclic “aRb, bRc, cRa is a “non-transitive trichotomous relation” (Sensagent, 2012). In the definition of an ordered integral domain or ordered field, the law of trichotomy is usually taken as more foundational than the law of total order, with y = 0, where 0 is the zero of the integral domain or field. In set theory, trichotomy is most commonly defined as a property that a binary relation “<” has when all its members “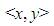 ” satisfy exactly one of the relations listed above. Strict inequality is an example of a trichotomous relation in this sense. Trichotomous relations in this sense are irreflexive and antisymmetric (Sensagent, 2012).
” satisfy exactly one of the relations listed above. Strict inequality is an example of a trichotomous relation in this sense. Trichotomous relations in this sense are irreflexive and antisymmetric (Sensagent, 2012).
“Trioinformatics Trichotomous Charge States Neuroengineered Neuromathematical Notation” provides a greater level of precision and an even more detailed rational foundation for the relationship between the elements and components of a trichotomous system in natural phenomena and the existing technology. The trioinformatics notation presented in this paper can be used in research investigations that involve multiple scientific disciplines, such as (but not limited to): electronic circuit design (as illustrated in “Trielectric Polyphase Systems” and “Tri-State Buffers” electronic circuit engineering (in the presentation of a trichotomous circuit designs (as illustrated and detailed in Figure 2); in a variety of psychometric (Rust and Golombok, 1989) instruments (as displayed in Figure 3); the sciences (in sections 3 and 4 and in the trichotomous research examples as displayed in “Trioinformatics: The innovative and novel logic notation that defines, explains, and expresses the rational application of the law of trichotomy for digital instrumentation and circuit design. That appears in imanager's March-May Journal on Circuits and Systems, Volume 3 (Number 2), pp. 1-7); and in the post hoc trichotomous statistical measures such as, Triostatistics (Osler, 2014). Through Trichotomous Charge States, the discipline of trioinformatics is greatly expanded in its scope and further defined in its universal applicability. As such TCS yields an applicability that has multiple uses in a wide variety of scientific arenas with countless viability, sustainable utility, and equitable usability.