The conceptualization of novel arenas of discovery through innovation and experimentation often yields new frames of reference used to define natural phenomena. Mathematical logic is a subfield of mathematics exploring the applications of formal logic to mathematics. It bears close connections to meta mathematics, the foundations of mathematics, and theoretical computer science (as stated by Boolos& Jeffrey (2002),Enderton& Enderton (2001), Mendelson (2009), and Shoenfield& Monk (2001)). According to Ferreirós, Mathematical logic emerged in the th mid-19 century as a subfield of mathematics independent of the traditional study of logic (Ferreirós 2001, p. 443). Mathematical logic is primarily a formal system that can be referred to as a “Deductive System”. A Deductive System (also called a deductive apparatus of a formal system) consists of the axioms (or axiom schemata) and rules of inference that can be used to derive the theorems of the system (Hunter,1973 ). Trichotomous logic as the core foundational infrastructure of the discipline of trioinformatics is a deductive system that provides the rationale for trichotomous research, inquiry, and logical trichotomous reasoning. In terms of the mathematical law of trichotomy, this can be expressed using “trichotomous logic” that is contained within the new discipline of “Trioinformatics”. Trioinformatics is the scientific discipline that specifically addresses and studies trichotomous logic and trichotomous logical data structures for the purposes of research and problem–solving. Trichotomous logic can parsimoniously be expressed as: Tri_[Logic] . The logic of trichotomy has its application in the trichotomous outcomes (“a,b, or c”) that are derived to express some unique or “universal” concept or idea. The universal concept or idea (for the specific purposes of trichotomous logic) is referred to as the “Universal Trichotomous Statement” (a “Cohesive Rational Statement” also identified by the acronym “U–Tri _[s]^"= Tri_[Logic] for the purposes of parsimony). The Universal Trichotomous Cohesive Rational Statement has the trichotomous logic expression of: Tri_{[a:b: or c]} because the variables “a, b, and c”. The trichotomous logic expression is equal to the UTCRS expression as they are both the same form of the same idea only one further defines and refines the idea in terms of implicit and explicit variation. Mathematically, this is conveyed in the subsequent trioinformatic trichotomous logic model:

(1)

The variables “a, b, and c” in trioinformatic trichotomous logic are enclosed within the enlarged brackets “[]” (though different in their respective positions, all the three are holistically a part of the same idea or concept; regarding the “Universal Trichotomous Statement”(the Cohesive Rational Statement) or “U–Tri_[s] ” which can also be expressed as, “Tri_{[a:b: or c]} ”). Thus, the brackets indicate that the variables (a, b, and c) are uniformly and directly related through a singular given statement, inquiry, and/or term for the specific purposes of determining an individual outcome (that is trichotomously “a, b, or c”). The logical mathematical notation for the decision–making process regarding the Universal Trichotomous Cohesive Rational Statement is of the following novel form,

(2)

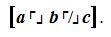
The aforementioned statement is pronounced as “Variable a opposed by Variable b and neither is Variable c”. Each of the terms represented in the logical notation of the mathematical law of trichotomy is defined as follows,

• [] = The “concentration on” “enclosure” symbol for a singular “Universal Trichotomous Statement” (the Cohesive Rational Statement) which is a trichotomous logic container(that has the Tri_{[a; b; or c]} statement enclosed within the U–Tri_[s] .
• a = The first variable in the given universal trichotomous cohesive rational statement for the mathematical notation of the logic of mathematical law of trichotomy.
• b = The second variable [that is opposite of the first given “variable a”] in the given universal trichotomous cohesive rational statement for the mathematical notation of the logic of mathematical law of trichotomy.
• c = The third variable [that is complete differentialor “absolute” of the first two given variables“a” and “b”] in the given universal trichotomous cohesive rational statement for the mathematical notation of the logic of the mathematical law of trichotomy.
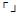• = The novel “antithetical” symbol is representative of “opposition” to the initially presented variable and uniquely designed trichotomous logical symbol for “opposed”, “opposed by” or “opposite” that literally means “mathematical opposites”, “mathematical opposing values” or “mathematically opposite variables” in the given universal trichotomous cohesive rational statement for the mathematical notation of the logic of the mathematical law of trichotomy.
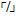• = The novel “closed antithetical” symbol is the representative of a “non-aligned neutral” and also a uniquely designed trichotomous logical symbol for “neither ” or “neither is” that literally means “mathematical differential negation” form the first two “opposing values” or “opposite variables” that were presented in the initially given universal trichotomous cohesive rational statement for the mathematical notation of the logic of the mathematical law of trichotomy.

In terms of mathematics, Apostol in his book on calculus defined “The Law of Tricohotomy” as: Every real number is negative, 0, or positive. The law is sometimes stated as “For arbitrary real numbers “a” and “b”, exactly one of the relations: (1.) a < b; (2.) a = b; and (3.) a > b, holds (Apostol, 1967). It is important to note that in mathematics, the law of trichotomy is most commonly the statement that for any (real) numbers x and y, exactly one of the following relations holds. Until the end of the 19^th century the law of trichotomy was tacitly assumed true without having been thoroughly examined (Singh, 1997). A proof was sought by Logicians and the law was indeed proved to be true. If applied to cardinal numbers, the law of trichotomy is equivalent to the axiom of choice. More generally, a binary relation R on X is trichotomous if for all x and y in X exactly one of xRy, yRx or x = y holds (Osler, 2013b). If such a relation is also transitive it is a strict total order, this is a special case of a strict weak order. For example, in the ≠≠case of three elements the relation R given by: (1.) aRb; (2.) aRc; and (3.) bRc is a strict total order. While the relation “R” given by the cyclic “aRb, bRc, cRa is a “non–transitive trichotomous relation” (Sensagent, 2012).In the definition of an ordered integral domain or ordered field, the law of trichotomy is usually taken as more foundational than the law of total order, with y = 0, where 0 is the zero of the integral domain or field. In set theory, trichotomy is most commonly defined as a property that a binary relation “<” has when all its members  satisfy exactly one of the relations listed above. Strict inequality is an example of a trichotomous relation in this sense. Trichotomous relations in this sense are irreflexive and antisymmetric (Sensagent, 2012).

The operative use of the mathematical notation of the logic of mathematical law of trichotomy requires that the eduscientist first create a “Universal Trichotomous Cohesive Rational Statement” that is applicable to some research inquiry. Consider the following scenario:

An engineer wishes to illustrate ternary application of a novel circuit design in terms of the logic gates of a new light–based integrated circuit. The circuit makes use of a silicon crystalline design with prisms and photons which are used to retrieve and store information. The CPU of this new machine uses a ternary computing model. The model has three primary functions illustrated as “On”, “Off” and “Hold” (or “Stasis”). The engineer has the following“Universal Trichotomous Statement” (which is the Cohesive Rational or Logic Statement) written are:“The three primary functions of the novel photon–driving electronic integrated circuit are “On” “Off” and “Hold”.”The statement would then be subsequently written by an engineer into a mathematically defined form in terms of a universal trichotomous cohesive rational statement as follows,

Tri_{[On; Off; or Hold]} = The primary functions of the new photon–based integrated circuit.

where,

On = “Power Accessible” = Trichotomous Logical Variable a.

Off = “Power Non–Accessible” = Trichotomous Logical Variable b.

Hold = “Power in Stasis (has Capacity)” = Trichotomous Logical Variable c.

In terms of practical usage, the given universal trichotomous cohesive rational statement would be rewritten in mathematical notation to take advantage of research parsimony. Thus, the newly written trichotomous logical statement makes full, efficient, and effective use of the mathematical notation of the logic of the mathematical law of trichotomy by the above mentioned eduscientist in the ensuing arrangement.

(3)

Therefore, shortened form of this statement is written,

(4)

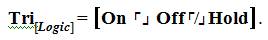
The statement above is then pronounced as “The Trichotomous Logical Concentration on On opposed by Off and neither is Hold”.

An example of a qualitative trichotomous cohesive rational statement for an in–depth classroom eduscientific (Osler, 2013a) inquiry (that actively makes use of trichotomous logic) is as follows: “As an active eduscientist a 4^th grade teacher has placed his 21 students in seven equal sized workgroups of three, he seeks to determine and measure classroom student perceptions at the end of first week of his classroom reorganization based on the following “Universal Trichotomous Statement” (which is the Cohesive Rational or Logic Statement) written are, “4^th Grade students placed into groups in classroom xyz in homeroom during the 20xx academic year perceive themselves as part of a group, as individuals or a members of an external group.”

The statement would then be subsequently written by the eduscientist into mathematically defined form in terms of a universal trichotomous cohesive rational statement as follows:

Tri_{[Us; I; or Them]} = 4^th Grade students placed into groups in classroom xyz in homeroom during the 20xx academic year perceive themselves as part of a group, as individuals, or a members of an external group.

Where,

Us = “Part of a Group” = Trichotomous Logical Variable a

I = “Individual” = Trichotomous Logical Variable b

Them = “Members of an External Group” = Trichotomous Logical Variable c.

In terms of practical usage, the given universal trichotomous cohesive rational statement would be rewritten in mathematical notation to take advantage of research parsimony. Thus, the newly written trichotomous logical statement makes full, efficient, and effective use of the mathematical notation of the logic of the mathematical law of trichotomy by the above mentioned eduscientist in the ensuing arrangement.

(5)

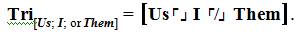
The shortened form of this statement is written,

(6)

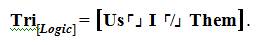
The statement above is then pronounced as “The Trichotomous Logical Concentration on Us opposed by I and neither is Them”.

An example of a qualitative trichotomous cohesive rational statement for an in–depth eduscientific inquiry (that actively makes use of trichotomous logic) is as follows: “An eduscientist seeks to measure the affective outcomes pertaining to faculty perceptions of the practical use a university course management system to disseminate course information. All of the members of the university faculty receive an online questionnaire related to the aforementioned topic via email. The following “Universal Trichotomous Statement” (which is the Cohesive Rational or Logic Statement)for the research regarding the topic is written as: “The response of university faculty towards the use of the university course management system for course information delivery for the xyz semester during the 20xx academic year is affirmation, negation or hesitation.”

The statement is then rewritten into the mathematical universal trichotomous cohesive rational statement.

Tri_{[Aff;Neg; or Hex]} = The response of university faculty towards the use of the university course management system for course information delivery for the xyz semester during the 20xx academic year is affirmation, negation or hesitation.

The mathematical “Universal Trichotomous Statement” (the Cohesive Rational Statement) (which can now be represented by the acronym“U–Tri_[s] ” = “Tri_[logic]”) is defined in this particular inquiry as follows:

Tri_{[Aff;Neg; or Hex]’} , where,

Aff = “Affirmation” (indicating a “Positive” overall response thereby representing a “Yes” reply) = Trichotomous Logical Variable a.

Neg= “Negation” (indicating a “Negative” overall response thereby representing a “No” reply) = Trichotomous Logical Variable b.

Hes = “Hesitation” (indicating a “Reclusive” overall response thereby representing a “Maybe” or a “Lack of” reply) = Trichotomous Logical Variable c.

In terms of this research question, the given universal trichotomous cohesive rational statement would once again be rewritten in mathematical notation to take advantage of research parsimony. Thus, the newly written trichotomous logical statement would have the following arrangement:

(7)

The shortened form of this statement is written,

(8)

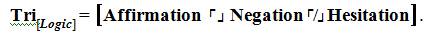
The statement above is then pronounced as “The Trichotomous Logical Concentration on Affirmation opposed by Negation and neither is Hesitation”.

The traditional academic sciences can find great value in trichotomous logic as it can be applied to many fields due its implicit nature that accurately describes the ternary nature inherent in natural phenomena. In the descriptions that follow trichotomous logic is applied to many different scientific fields that are foundational to electronics and circuit design. As such, the use of trioinformatics in terms of the primary science that form the foundations of structure in materials science and engineering (also in electronics and digital signal processing in particular), trichotomous logic can be applied in the following manner:

• Space (also referred to as “True Space”, “Positive Space” or “Real Space” [i.e., “Reality”]), is represented by the numeric value = (+1).
• Anti–Space (also termed “Counter Space”, i.e., “Negative Space” or“Opposite Space”) is represented by the numeric value = (–1).
• Non–Space (also called “No Space”, “Occupied Space”, or “Filled Space”) is represented by the numeric value = (0).

Thus, the trichotomous logical statement in terms of structure in materials science and engineering would have the following arrangement:

(9)

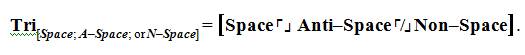
The shortened form of this statement is written,

(10)

The statement above is then pronounced as “The Trichotomous Logical Concentration on Space opposed by Anti–Space and neither is Non–Space”.

In terms of physician deference to material existence trioinformatic trichotomous logic can be applied in the following manner,

a.) Matter
b.) Anti–Matter and
c.) No Matter (or “Empty Space”).

Thus, the trichotomous logical statement in terms of structure in materials science and engineering would have the following arrangement:

(11)

The shortened form of this statement is written,

(12)

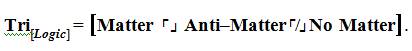
The statement above is then pronounced as “The Trichotomous Logical Concentration on Matter opposed by Anti-Matter and neither is No Matter”.

In addition, in terms of the nature-based science of physics in reference to “sub–atomic particle structure” trioinformatic trichotomous logic can be applied in the following manner,

a.) Proton,
b.) Electron, and
c.) Neutron.

Thus, the trichotomous logical statement in terms of structure in materials science and engineering would have the following arrangement:

(13)

The shortened form of this statement is written,

(14)

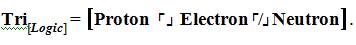
The statement above is then pronounced as “The Trichotomous Logical Concentration on Proton opposed by Electron and neither is Neutron”.

Within the discipline of physics in regards to anti– materialistic antiparticle antimatter structure trioinformatic trichotomous logic can be applied in the following manner,

a.) Anti proton
b.) Positron (or “Anti electron”)and
c.) Anti neutron.

Thus, the trichotomous logical statement in terms of structure in materials science and engineering would have the following arrangement:

(15)

The shortened form of this statement is written,

(16)

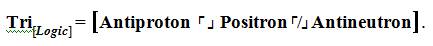
The statement above is then pronounced as “The Trichotomous Logical Concentration on Antiproton opposed by Positron and neither is Antineutron”.

In terms of electronic frequency (expressions of the three types of energy–wave transference) trichotomous logic can be applied in the following manner,

a.) Transverse Wave Pattern (“Latitudinal Waves”, “Up and Down Waves”, or “Aboveand Below Waves”) =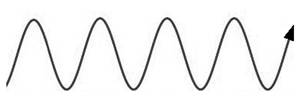
b.) Transitional Wave Pattern (“Longitudinal Waves” or “Left to Right Waves” or “Side to Side Waves”) = and
c.) Torsional Wave Pattern (“Twisting Waves” or “Rotating Waves” or “Vortex Waves”) =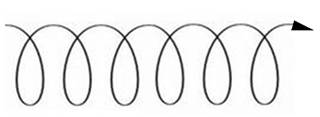

Thus, the trichotomous logical statement in terms of structure in materials science and engineering would have the following arrangement:

(17)

The shortened form of this statement is written,

(18)

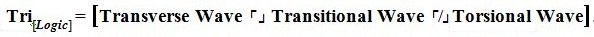
The statement above is then pronounced as “The Trichotomous Logical Concentration on Transverse Wave opposed by Transitional Wave and neither is Torsional Wave”.

Trioinformatics trichotomous logic procedures provide a rational foundation for the relationship between the elements and components of a trichotomous system. In addition to trichotomous systemic representations, trioinformatics provides a detailed explicative methodology for a variety of investigative inquiries into natural phenomena and the sciences. The trioinformatics trichotomous logic method presented in this paper can be used in research investigations that involve a plethora of scientific disciplines. Some examples are Electronic Circuit Engineering (in the presentation of a trichotomous circuit designs as illustrated earlier in the first trichotomous logic example displayed in the “Practical Use of Trioinformatics” section), Psychometric (Rust and Golombok, 1989) Instruments, Sciences (in the trichotomous logic examples shown in the “The Use of Trioinformatics in Physics” section) Trichotomous Metrics (such as the Tri–Squared Test and its associated “Inventive Investigative Instrumentation”) (Osler, 2012) and in post hoc trichotomous statistical measures such as Triostatistics (Osler, 2014). Thus, trioinformatics is a novel and innovative discipline that has universal applicability in a wide variety of scientific areas and arenas with unlimited possibilities, utility, and usability.