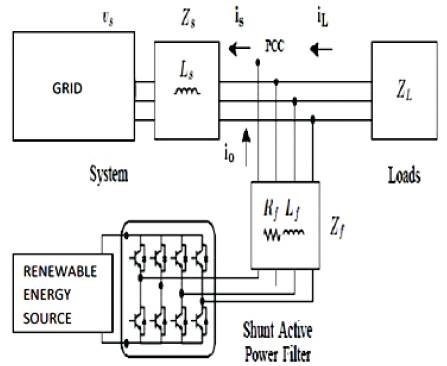
Figure 1. Schematic diagram of renewable based distributed generation system
This paper suggests an active power filter implemented with a four leg voltage-source inverter using DQ (Synchronous Reference Frame) based Current Reference Generator scheme. The use of a four-leg voltage-source inverter allows the compensation of current harmonic components, as well as unbalanced current generated by single-phase non-linear loads. The grid interfacing can thus be utilized as:1) Power Converter to inject power generated from rest of the grid, and 2) Shunts APF to current unbalance, load current harmonics and load reactive power demand. The compensation, performance of the proposed active power filter using an adaptive fuzzy controller and the associated control scheme under steady state and transient operating conditions are demonstrated through simulation results.
The widespread use of non-linear loads is leading to a variety of undesirable phenomena in the operation of power systems. The harmonic components in current and voltage waveforms are the most important among these. Conventionally, passive filters have been used to eliminate line current harmonics. However, they introduce resonance in the power system and tend to be bulky. So active power line conditioners have become more popular than passive filters as it compensates the harmonics and reactive power simultaneously. The active power filter topology can be connected in series or shunt and combinations of both. Shunt active filter is more popular than series active filter because most of the industrial applications require current harmonic compensation. Different types of active filters have been proposed to increase the electric system quality; a generalized block diagram of active power filter is presented in [2]. The classification is based on following criteria.
Current controlled voltage source inverters can be utilized with an appropriate control strategy to perform an active filter functionality. The electrical grid will include a very large number of small producers that use renewable energy sources, like solar panels or wind generators. One of the most common problems when connecting small renewable energy systems to the electric grid concerns the interface unit between the power sources and the grid, because it can inject harmonic components that may detoriate the power quality [1],[2]. However, the extensive use of power electronics based equipment and non-linear loads at PCC generate harmonic currents, which may deteriorate the quality power. In[3] an inverter operates as active inductor at a certain frequency to absorb the harmonic current. A similar approach in which a shunt active filter acts as active conductance to damp out the harmonics in the distribution network is proposed in[4],[5].
The proposed system consists of RES connected to the DClink of a grid-interfacing inverter as shown in Figure 1. The voltage source inverter is a key element of a DG system as it interfaces the renewable energy source to the grid and delivers the generated power. The RES may be a DC source or an AC source with rectifier coupled to dc-link. Usually, the fuel cell and photovoltaic energy sources generate power at variable low DC voltages, while the variable speed wind turbines generate power at variable AC voltage. Thus, the power generated from these renewable sources needs power conditioning (i.e., dc/dc or ac/dc) before connecting on dc-link [6]–[8]. The dc-capacitor decouples the RES from grid and also allows independent control of converters on either side of dc-link.

Figure 1. Schematic diagram of renewable based distributed generation system
The four-leg PWM converter topology is shown in Figure 2. This converter topology is similar to the conventional three phase converter with the fourth leg connected to the neutral bus of the system. The fourth leg increases switching states from 8 (23) to 16 (24), improving control, flexibility and output voltage quality, and is suitable for current unbalanced compensation.

Figure 2. Two-level four-leg PWM-VSI topology
The voltage in any leg x of the converter, measured from the negative point of the dc-voltage (N), can be expressed in terms of switching states, as follows:
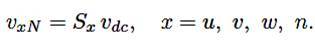
The mathematical model of the filter, derived from the equivalent circuit shown in Figure 1, is
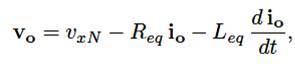
where Req and Leq are the 4L-VSI output parameters, expressed as Thevenin impedances at the converter output terminals, Zeq . Therefore, the Thevenin equivalent impedance is determined by a series connection of the ripple filter impedance Zf and a parallel arrangement between the system equivalent impedance Zs and the load impedance ZL (3).
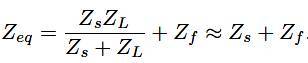
In this model, it is assumed that ZL >> Zf, that the resistive part of the system's equivalent impedance is neglected, and that the series resistance is in the range of 3-7% p.u., which is an acceptable approximation of the real system. Finally, in equation (2) Req = Rf and Leq = Ls + Lf.
A dq-based current reference generator scheme[9]-[14] is used to obtain the active power filter current reference signals. This scheme presents a fast and accurate signal tracking capability. This characteristic avoids voltage fluctuations that deteriorate the current reference signal affecting compensation performance. The current reference signals are obtained from the corresponding load currents as shown in Figure 3. This module calculates the reference signal currents required by the converter to compensate reactive power, current harmonic and current imbalance. The displacement power factor (sin(L) )and the maximum total harmonic distortion of the load (THD(L) )defines the relationships between the apparent power required by the active power filter, with respect to the load, as shown in below equation.
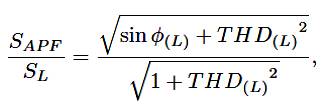
where the value of THD(L) includes the maximum compensable harmonic current, defined as double the sampling frequency fs. The frequency of the maximum current harmonic component that can be compensated is equal to two times the converter switching frequency.
The dq-based scheme operated in a rotating reference frame[15]-[17]; therefore, the measured currents must be multiplied by the sin(wt) and cos(wt) signals. By using dqtransformation, the d current component is synchronized with the corresponding phase-to-neutral system voltage and the q current components are phase-shifted by 90◦. The sin(wt) and cos(wt) synchronized reference signals are obtained from a Synchronous Reference Frame (SRF) PLL. The SRF-PLL generates a pure sinusoidal waveform even when the system voltage is severely distorted. Tracking errors are eliminated, since SRF-PLLs are designed to avoid phase voltage unbalancing, harmonics (i.e. less than 5% and 3% in 5th and 7th respectively), and offset caused by the nonlinear load conditions and measurement errors.
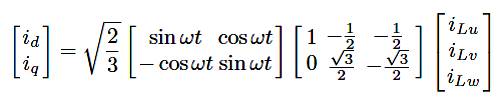
A Low-Pass Filter (LFP) extracts the dc component of the phase-currents id to generate the harmonic reference component id . The reactive reference components of the phase currents are obtained by phase-shifting the corresponding AC and dc components of iq by 180◦. In order to keep the dc voltage constant, the amplitude of the converter reference current must be modified by adding an active power reference signal (ie) with the d- component. The resulting signals i*d , and i*q are transformed back into a three-phase system by applying the inverse Park and Clark transformation, The cutoff frequency of the LPF used in this paper is 20 Hz.
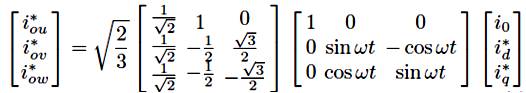
The current that flows through the neutral of the load is compensated by injecting the same instantaneous value obtained from the phase-currents, phase-shifted by 180◦, as shown below.

One of the major advantages of the dq-based current reference generator scheme is that it allows the implementation of a linear controller in the dc-voltage control loop. However, one important disadvantage of the dq-based current reference frame algorithm used to generate the current reference is that a second order harmonic component is generated in id and iq under unbalanced operating conditions. The amplitude of this harmonic depends on the percent of unbalanced load current (expressed as the relationship between the negative sequence current iL ,2 and the positive sequence current iL ,1 ). The second order harmonic cannot be removed from id and iq , and therefore generates a 3rd harmonic in the reference current when it is converted back to abc frame. The scheme shows the percent of system current imbalance and the percent of 3rd harmonic system current, in function of the percent of load current imbalance [18], [19]. Since the load current does not have a 3rd harmonic, the one generated by the active power filter flows to the power system.
The dc-voltage converter is controlled by a traditional Fuzzy controller [20]. This is an important issue in the evaluation, since the cost function is designed using only current references, in order to avoid the use of weighting factors. Generally, these weighting factors are obtained experimentally, and they are not well defined when different operating conditions are required. Additionally, the slow dynamic response of the voltage across the electrolytic capacitor does not affect the current transient response. For this reason, the Fuzzy controller represents a simple and effective alternative for the dc-voltage control.
The disadvantage of PI controller is its inability to react to abrupt changes in the error signal, ε, because it is only capable of determining the instantaneous value of the error signal without considering the change of the rise and fall of the error, which in mathematical terms is the derivative of the error denoted as Δε. To solve this problem Fuzzy logic control[21] as it is shown in Figure 4 is proposed.
The determination of the output control signal, is done with an inference engine with a rule base having if-then rules in the form of,
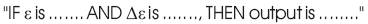
With the rule base, the value of the output is changed according to the value of the error signal ε, and the rate-oferror Δε. The structure and determination of the rule base is using trial-and-error methods, and is also done through experimentation.
All the variable' fuzzy subsets for the inputs ε and Δε are defined as (NB, NM, NS, Z, PS, PM, PB). The membership function of inputs and output are illustrated in Figures 5 and 6, and output in Figure 7. The fuzzy control rule is illustrated in Table1.
A simulation model for the three-phase four-leg PWM converter with the parameters shown in Table 2 has been developed using MATLAB-Simulink. The objective is to verify the current harmonic compensation effectiveness of the proposed control scheme under different operating conditions. A six pulse rectifier was used as a non-linear load.
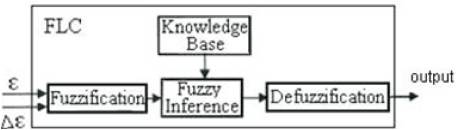
Figure 4. Basic representation of FLC
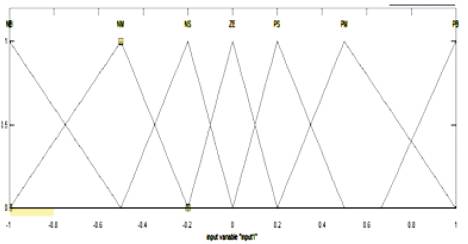
Figure 5. Membership functions of input Ɛ

Figure 6. Membership functions of input ΔƐ
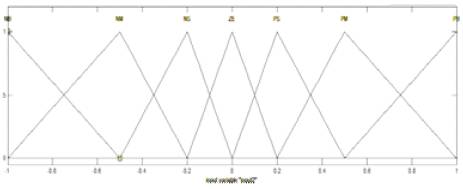
Figure 7. Membership functions of output Ɛ and ΔƐ

Table. 1 FLC Rule Base
In the simulated results shown in Figures 8-15, the active filter starts to compensate at t =0.2. At this time, the active power filter injects an output current iou to compensate current harmonic components, current unbalanced, and neutral current simultaneously. During compensation, the system currents (is) show sinusoidal waveform, with low total harmonic distortion. At t =0.4, a three-phase balanced load step change is generated from 0.6 to 1.0 p.u. The compensated system currents remain sinusoidal despite the change in the load current magnitude. Finally, at t =0.6, a single-phase load step change is introduced in phase u from 1.0 to 1.3 p.u., which is equivalent to an 11% current imbalance. As expected on the load side, a neutral current flow through the neutral conductor (iLn), but on the source side, no neutral current is observed (isn). Simulated results show that the proposed control scheme effectively eliminates unbalanced currents. Additionally, results show that the dc-voltage remains stable throughout the whole active power filter operation.

Table 2. Specification Parameters

Figure 8. Phase to neutral source voltage
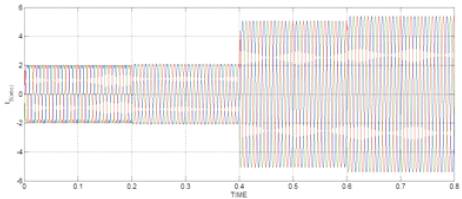
Figure 9. Source currents
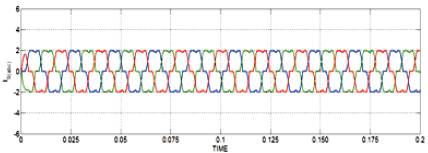
Figure 10. Source currents at 0 < t < 0.2
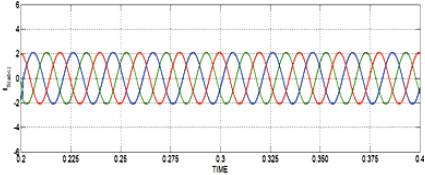
Figure 11. Source currents at 0.2 < t < 0.4

Figure 12. Source currents at 0.4 < t < 0.6
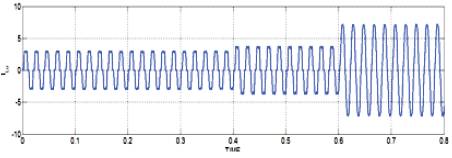
Figure 13. Load current
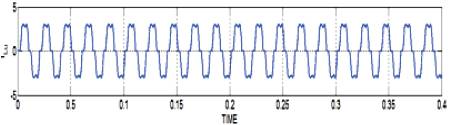
Figure 14. Load current at 0 < t < 0.4

Figure 15. Load current at 0.4 < t < 0.6
Improved dynamic current harmonics and a reactive power compensation scheme for power distribution systems with generation from renewable sources has been proposed to improve the current quality of the distribution system. Advantages of the proposed scheme are related to its simplicity, modeling and implementation. The MATLAB/SIMULINK simulation model of the proposed system with the connection of renewable energy sources is shown and validated. The use of a dq-based current reference generation scheme for the converter current loop proved to be an effective solution for active power filter applications, improving current tracking capability and transient response. Simulated results have proved that the proposed control method is a good alternative to classical linear control methods. Simulated results have shown the compensation effectiveness of the proposed active power filter.