
Hyperboloidal shell structures have applications like cooling towers in thermal power plants. These types of structures have complex geometry and may lead to the failure because of its imperfections in geometry, when subjected to horizontal loads. Geometrical optimization of such structures leads to minimum stresses and deflections and finds out best possible load bearing behavior. This paper deals with the modal analysis of hyperboloidal shell structures of two different heights (143.5 m and 175.5 m). The hyperboloidal shells are modelled by varying height to top diameter ratio (1.5, 1.75, 2.0, 2.25, 2.5) and height to bottom diameter ratio (1.3, 1.35, 1.4, 1.45, 1.5). Free vibration analysis has been carried out for all the models described above to obtain the fundamental natural time periods / frequencies and mode shapes. This analysis has been carried out using ANSYS and finally, some useful conclusions are drawn.
Hyperboloidal shell structures have numerous applications like cooling towers, roofs and are used in atomic and thermal power plants, which produce electricity/heat. The hyperboloidal structure has an advantage of negative gaussian curvature, which makes it predominant in stability against external loads. A cooling tower is an encased structure, intended for the cooling of water, where high temperature water gets cooled by getting immediate contact with barometrical air. Most of cooling towers take hyperboloidal shape in order to maximize the area where the diffusion takes place so that hot air mixes very fast and refrigeration of water is done more effectively. In order to support the tall structure with minimal thickness, the tower has consolidated bottom. These towers are specially designed to keep the equipment cool enough to operate efficiently, without causing an excess amount of pollution. Hyperboloidal structures are usually up to 200 m long and 100 m in width or rectangular frame works are generally greater than 40 m tall and 80 m in width.
Nasir, Thambiratnam, Butler, and Austin (2002) have investigated the free vibration and seismic response of axisymmetric shell structures. They examined the influence of curvature, height, and thickness, when subjected to earthquake loading. They concluded that with an increase in curvature, the period of vibrations is decreasing, but the trend is reversing in case of high curvatures. They have also concluded that height is an important factor in the transient earthquake analysis.
El Ansary, El Damatty, and Nassef (2011) developed a numerical tool based on nonlinear finite element method and genetic algorithm optimization technique, which is capable of achieving an optimum design and shape of hyperbolic cooling tower. They found out the optimum shape of the tower corresponding to least weight for the given thickness. They concluded that the proposed genetic algorithm technique leads to about 12% reduction in weight of the tower.
Ponath and George (2016) have studied cooling towers with different heights and varying thickness. They have modelled the tower using ABAQUS. They have performed the static and buckling analysis. They concluded that the maximum stress occurs near the base due to changes in the vertical profile. Tower with greater height have critical buckling load on account of larger thickness of the shell.
Athira, Rahul, Sivan, Vijayan, and Sabu (2016) carried out the design and estimation of an existing cooling tower at Dahej, Gujarat. They compared the seismic analysis methods, such as equivalent static, response spectrum, and time history method. From their study, they concluded that the time history analysis is more accurate to study the structural response when compared with others.
Casucci, Andres, and Wörmann (2016) have studied the behavior of hyperbolic cooling towers under the dynamic excitation of earthquakes. Three different kinds of supporting columns were examined and compared. Their study included in the parametric analyses considering different locations and soil conditions and also comparing on different kinds of columns. The following conclusions were made by the authors that due to temperature loads and higher spacing at lower lintel, the radial columns are the less statically efficient, which confer maximum stresses and bending moment to the shell and to the columns. They have also concluded for best seismic performance A and V columns need an additional reinforcement. Their results summarised that V columns are expensive than other orientations, but they are the most suitable type column in regions, which have less intensity of earthquakes.
Mahdavi, Davoodi, and Mostafavian (2012) have studied the three story steel frame, whose joints were bolted. Joint stiffness is used as a variable in their study. The impact model which is used for testing consists of an impact hammer, a spectrum analyzer, and an accelerometer.
Viladkar, Godbole, and Krishna (1998) have proposed a new model to perform finite element analysis on hyperbolic cooling towers, which is much more accurate than the earlier models. The towers are generally rested on the annular ring of adjacent columns, which creates and intermittent reactions at the tower's base. In most of the earlier FEM models, the A-frame columns, which support the towers are ignored and instead, the bottom of the tower is fixed. In practical cases, such condition will not depict an accurate model of a hyperbolic tower, and the results are compromised. So as to avoid this, the tower which is supported by columns is also considered in the boundary conditions along with the shell body by using semi-loof elements. The hyperboloid tower is represented by semiloof shell elements. It was found that the membrane forces which are away from the bottom part of the tower are not much affected by a change in boundary condition. A significant difference was found at the lower part of the tower with respect to membrane forces. The results are found to be promising as the proposed model is an actual and a better physical representation of the cooling tower.
Angelides (2016) had studied on different columns configurations and their connections to the shell. His work addressed on different column configurations such as "V", "X" and meridional column arrangements. These towers have been analysed for severe earthquake motions and the issue of retrofit of existing cooling towers with particular emphasis on the rehabilitation and strengthening of the shell supporting columns is also considered in his study. The conclusions were made by the author that the meridional arrangement of columns are not well suited for higher seismic action, due to the high bending moments and sensitivity to torsional vibration modes. He also stated that the V-column arrangement is better suited for seismic action, which is resisted by a combination of axial forces and bending moments developing at the column ends.
Nangshineh, Alavi, and Rezaee (2013) studied the effect of lateral loads such as wind and seismic loads on a hyperbolic cooling tower of varying thickness and dimensions. They considered three models of cooling tower by taking one tower as a reference from an existing power plant and compared the other two models with respect to reference tower. They analyzed the cooling tower for seismic loading and wind loading using ANSYS software. Their study revealed that the design parameters have lots of influence on deflections and stresses.
Kulkarni and Kulkarni (2014) carried out the modal analysis of hyperbolic towers. In their case study as reference, two existing towers from the bellari thermal power station are chosen (143.5 m and 175.5). They carried out analysis using FEA based ANSYS software and in the analysis shell 93 elements are considered. According to their study, modal analysis shows that as thickness increases maximum prinicipal stress increases and there is a shift in the stress concentration from neck to bottom as mode value increases. They have also concluded that as the value is increasing from 200 to 500, deflection got decreased in the fundamental mode and deflections are almost same for 250-450 mm thickness for two towers in mode 5.
Gaikwad, Gore, Sayagavi, Madhavi, and Pattiwar (2014) have studied the effect of lateral loading such as wind on natural draught hyperbolic cooling tower. They studied the cooling tower with the V-shape configuration of Raker column. Their study revealed that response parameters, such as hoop stresses, in-plane shear, maximum and minimum principal stresses, and period of vibration increases significantly with increase of height.
Castiau and Gaurois (1991) carried out the design of the Ohaaki cooling tower in New Zealand. They made a comparative study between the actual design and alternative designs for structures, when subjected to severe earthquake conditions. In their research work, they compared the actual diagonals of the structure and alternative diagonals provided to it. They have concluded that meridional supports are slightly heavier than others and SRSS responses are 10 to 20% higher than the original supports of the structure.
He, Moaveni, Conte, Elgamal, and Masri (2009) carried out dynamic field test on the Alfred zampa Memorial bridge before the bridge opened up to traffic. Dynamic field tests provide a good chance to understand the modal properties of the bridge in its initial conditions without any kind of loads acting on it. Modal identification was done using three methods in their study, i.e., 1. The multiplereference natural excitation technique in combination with the Eigen system realization algorithm 2. The data-driven stochastic subspace identification 3. The enhanced frequency domain decomposition method. The modal damping ratios identified from forced vibration test data are higher than those estimated from ambient vibration data.
Yong and Lin (1985) have studied the free vibration analysis, seismic, and wind excitation on column supported cooling towers. Wind pressures are applied as static and fluctuating pressures. They have developed an algorithm to compute the free and forced vibrations. In case of wind excitations, they have concluded that for each circumferential mode number, the fluctuation art is dominated by the second mode rather than first mode.
Vhanungare and Angalekar (2016) carried out the finite element analysis of hyperboloidal shell by the concept of equivalent plate. They have analyzed the tower for with alternative I and V supports. Their investigation showed that the V supports showed sway of more than 90% at the top level and throat level of tower compared to I supports.
Ballari Warm Power Station (BTPS) is a power producing plant near to Kudatini town in Ballari district, Karnataka state. Two existing hyperboloidal cooling towers are analyzed in this research work. The total height of the towers is 143.5 m (designated as H1) and 175.5 m (designated as H2) with constant shell wall thickness of 200 mm, constructed of RCC. The geometry of Hyperboloid of revolution can be expressed as,

where, Ro is the horizontal radius at any vertical co-ordinate and as radius at throat level, b is the dimension of hyperboloid shell, and H is the origin of co-ordinate being defined by the center of the tower throat 4-noded shell 63 elements, which has six degrees of freedom at each node, bending and membrane capabilities has been chosen to model the complex geometry. In addition to the existing two towers, various towers are modelled by varying the H/db and H/debt ratios in this present study. The geometrical parameters of the hyperboloidal shell of height 143.5 m with H/Dt 1.5, 1.75, 2, 2.25, and 2.5 are listed in Table 1 and are shown in Figures 1 - 5. Similarly, the geometrical parameters of the hyperboloidal shell structure of height 175.5 m with similar H/Dt are modelled and analyzed.
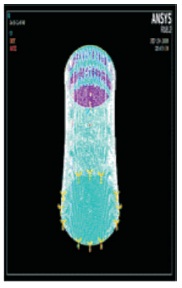
Figure 1. FE Model of H1-T-1.5
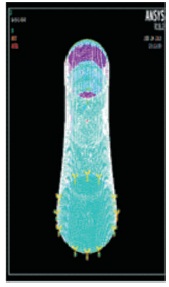
Figure 2. FE Model of H1-T-1.75

Figure 3. FE Model of H1-T-2.0

Figure 4. FE Model of H1-T-2.25

Figure 5. FE Model of H1-T-2.5
Free vibration analysis has been carried out in the above said models in ANSYS. Time Periods were obtained and are listed in Table 2. The fundamental mode shape of the hyperboloidal shell structure having as H/Dt ratio 1.5, 1.75, 2, 2.25, and 2.5 are shown in Figures 6 - 10. The variation of Time period with various H/Dt ratios 1.5, 1.75, 2, 2.25, and 2.5 for heights of 143.5 m and 175.5 m are graphically represented in Figures 11 and 12, respectively.
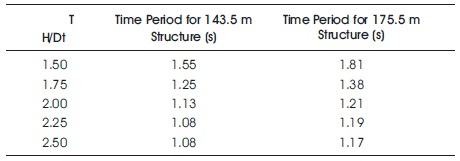
Table 2. Time Periods of Hyperboloidal Shell Structure of Height 143.5 m and 175.5 m

Figure 6. Fundamental Mode Shape of H1-T-1.75
Figure 7. Fundamental Mode Shape of H1-T-2.0

Figure 8. Fundamental Mode Shape of H1-T-1.5

Figure 9. Fundamental Mode Shape of H1-T-2.25
Figure 10. Fundamental Mode Shape of H1-T-2.5
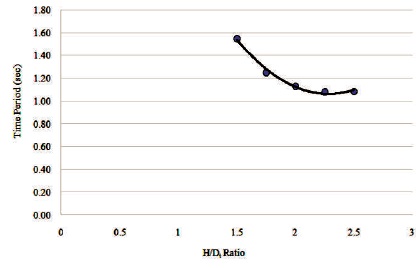
Figure 11. Variation of Time Period with H/Dt for143.5 m ht. Structure
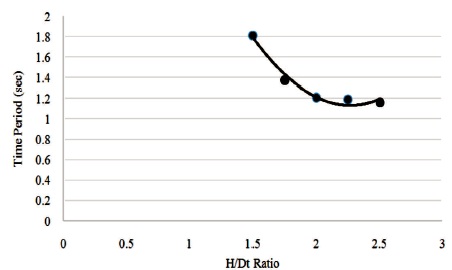
Figure 12. Variation of Time Period with H/Dt for 175.5 m ht. Structure
The geometrical parameters of a hyperboloidal shell of height 143.5 m with H/Db ratios 1.3, 1.35, 1.4, 1.45, and 1.5 are listed in Table 3 and are shown in Figures 13 - 17. Similarly, the geometrical parameters of the hyperboloidal shell structure of height 175.5 m with similar H/Db are modelled and analyzed.
Figure 13. FE Model of H1-B-1.3
Figure 14. FE Model of H1-B-1.35

Figure 15. FE Model of H1-B-1.4
Figure16. FE Model of H1-B-1.45
Figure 17. FE Model of H1-B-1.5
Free vibration analysis has been carried out for the above listed models in ANSYS. Time Periods were obtained and are listed in Table 4. The fundamental mode shape of the hyperboloidal shell structure having H/Db ratio 1.3, 1.35, 1.4, 1.45, and 1.5 are shown in Figures 18 - 22. The variation of Time period with various H/Dbratios 1.3, 1.35, 1.4, 1.45, and 1.5 for heights of 143.5 m, and 175.5 m graphically represented in Figures 23 and 24, respectively.
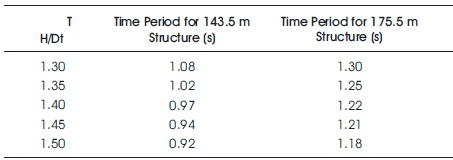
Table 4. Time Periods of Hyperboloidal shell Structure of Height 143.5 m and 175.5 m

Figure 18. Fundamental Mode Shape of H1-B-1.3
Figure 19. Fundamental Mode Shape of H1-B-1.35
Figure 20. Fundamental Mode Shape of H1-B-1.4
Figure 21. Fundamental Mode Shape of H1-B-1.45

Figure 22. Fundamental Mode Shape of H1-B-1.5

Figure 23. Variation of Time Period with H/Db for 143.5 m ht. Structure
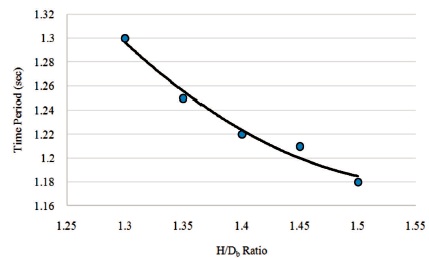
Figure 24. Variation of Time Period with H/Db for 175.5 m ht. Structure
As the H/Dt ratio increases from 1.5 to 2.5, it is observed that the time periods are reduced by 30.3%. As the H/Db ratio increases from 1.3 to 1.5, time periods are reduced by 14.8%.
As the H/Dt ratio increases from 1.5 to 2.5, it is observed that the time periods are reduced by 35.4%. As the H/Db ratio increases from 1.3 to 1.5, time periods are reduced by 9.2%.
The following conclusion are drawn from the study.