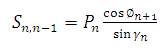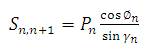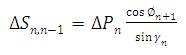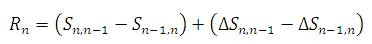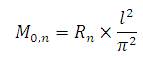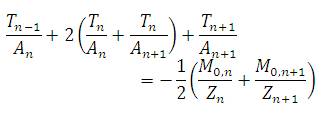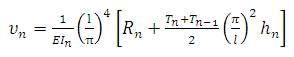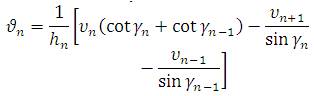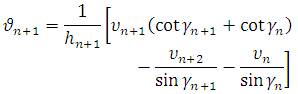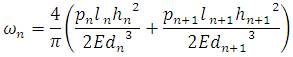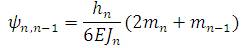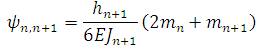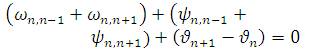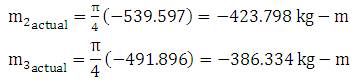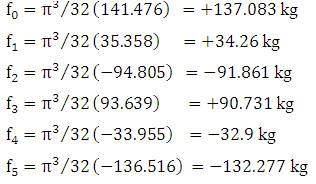One of the principle features of current civil engineering construction is to save structural material without affecting the durability of the structure. This highlights the use of thinwalled structures in all countries. The first and foremost terminology we should understand is stressed-skin structures. Stressed-skin structures are the type of structures that tend to carry loads primarily by direct stresses, acting in their plane due to their geometry and small flexural rigidity of the skin. This concept is mainly used in structures where maximum space and minimum weight are of primary concerns and also can be used to some stationary structures. Folded plates and shells belong to the class of stressed-skin structures.

Shells can be defined as curved structures capable of transmitting load in more than two directions to support.

Folded plates are assemblies of flat plates rigidly connected together along their edges in such a way so as to make the structural system capable of carrying loads without the need for additional supporting beams along the mutual edges. These are also called as Hipped Plates. Each plate is assumed to act as a beam in its own plane; this assumption is justified when the ratio of the span “length” of the plate to its height “width” is large enough. But when this ratio is small, the plate behaves as a deep beam.

Folded plate structures provide an economical and aesthetically pleasing solution to the problem of roofing large areas. These structures have aroused attention in recent years because of their economic advantage and aesthetical appearance. Compared to shells these structures usually consume slightly more materials, but this disadvantage is often offset by the simpler formwork required for their construction. They offer more advantages than complex structures, such as cylindrical shells, arches and frames. Longer spans may be obtained due to inherent stiffness without an increase in material requirement.

1.1 Applications of Folded Plates

• Folded plates have been used for various buildings like ware houses, swimming pools, gymnasium, offices, shopping malls, entrances to buildings and tunnels, bridges, retaining walls etc..
• These are widely used as roofs in industrial buildings.

A northlight folded plate roof shown in Figure 1 and Figure 2 is analyzed for the longitudinal stresses and the transverse moments for the following data [7].

• Span of the northlight folded plate(l) is taken as 20 m.
• Height of the northlight folded plate(H) is considered as 2m.
• Thickness of northlight folded plate (d) is taken as 10.16 cm.
• Inclination of inclined plate is considered as 40°.
• Density of reinforced cement concrete is taken as 25 kN/m³ [8].
• Live load on the structure is considered as per IS 875- 1997 reaffirmed part 2 as 0.75 kN/m² [9] .
• Projection of sunshade is taken as 30 cm.
• Thickness of sunshade is considered as 10.16 cm.

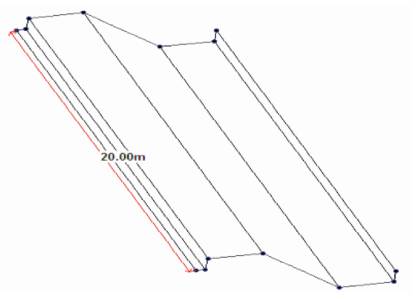
Figure 1. Longitudinal View of Northlight Folded Plate

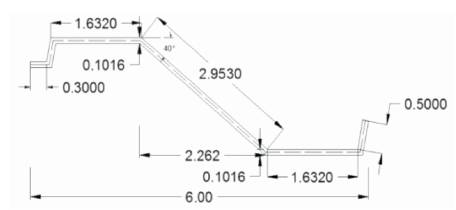
Figure 2. Cross-section of the Northlight Folded Plate

Whitney method of analysis was used for analysis of the northlight folded plate. Whitney considered the end plates of the folded plate as cantilevers. This is a simplified treatment of folded plates due to which the number of simultaneous equations to be solved is reduced by two. The Whitney method is applicable for folded plates with width and thickness of the plates and the intensity of loading uniform along the length of the plate. Mathematical computations are greatly simplified by replacing the uniform load by Fourier loading and considering only the first term of the series. The plate moments, stresses and deformations, therefore, vary as sine functions along the length, have maximum values at mid span.

1. Plate loads were calculated by [10].

(1)

(2)

2. Additional plate loads were calculated by :

(3)

3. Additional plate loads were calculated by :

(4)

(5)

4. Resultant plate loads were calculated by :

(6)

5. Plate moments were calculated by :

(7)

6. Edge – Shear equations were established using the formula :

(8)

7. Plate deflections were calculated by :

(9)

8. Angle changes due to plate deflection were calculated by :

(10)

(11)

9. Angle changes due to loads were calculated by :

(12)

10. Angle changes due to transverse moments were calculated by :

(13)

(14)

11. The transverse moments of each plate were computed by considering the total change at each joint which is equal to zero.

(15)

From these values we arrive at the fiber stresses at the other sections, noting that their distribution along the span follows a sine curve. Then the fiber stresses are corrected by multiplying by the factor 1 π³/32. This correction is applied as only the first term of Fourier series has been used.

The northlight folded plate roof structure was modeled using four noded plate elements in STAAD. Pro, and each node has six degrees of freedom. The folded plate can be modeled as a single block as a whole, but application of loads over the plate as well as the study and analysis at intermediate points is a difficult task. In order to study the performance at various critical points, folded plate was modeled as a fine division of the folded plate into finite elements. The discretization of folded plate into finite elements can be done into any number of parts. Discretization of the folded plate into elements should be such that the element of the folded plate should represent the shape of the folded plate. In the present study, the folded plate was discretized at 1 meter interval as shown in Figure 3. Details, Geometrical, Trigonometric of the Northlight Folded Plate are shown in Tables 1, 2, and 3.

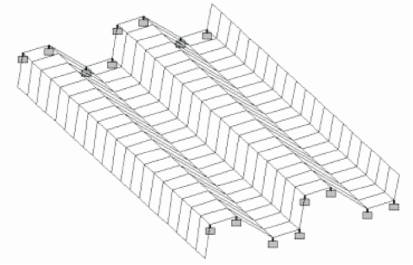
Figure 3. Modelling of the Northlight Folded Plate

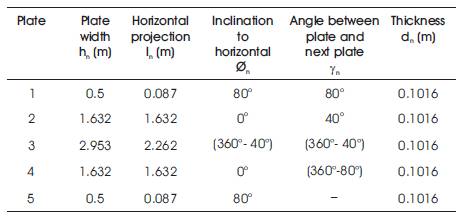
Table 1. Details of the Northlight folded plate

Table 2. Geometrical Properties of Northlight folded plate

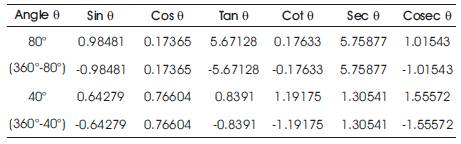
Table 3. Trigonometric Properties of Northlight folded plate

• The northlight folded plate was modeled by assigning nodes and joining the nodes using four noded plate elements.
• Now the folded plate structure was discretized into rectangular elements by generating plate mesh at 1 meter interval longitudinally.
• Material was assigned to the plate, and the material properties like density of material, modulus of elasticity, Poisson's Ratio, were assigned for all plate elements.
• Thickness of the plate was assigned and the fixed supports for selected nodes were assigned.
• Ridge loads were applied on nodes and the analysis command was given to run the analysis. Data supplied is to be processed to complete structure.
• After assigning the loads, Performance of analysis is done.
• Post processing results in stresses, displacements, moments of the folded plate model, were studied.

Using dead load and live load, total load was calculated. From total load, ridge load acting at nodes was determined. As the analysis of a northlight folded plate was based on a mathematical approach, the ridge loads were assigned to nodes in the STAAD. Pro, directly as shown in Figures 4,5,6,7 and 8.

Figure 4. Ridge Load 327.291 kg

Figure 5. Ridge Load 1302.325 kg

Figure 6. Ridge Load 1232.091 kg

Figure 7. Ridge Load 315.632 kg

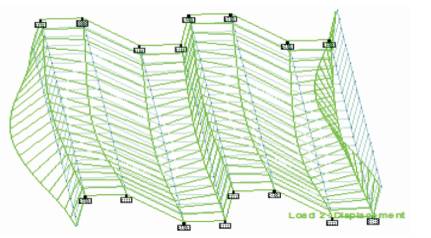
Figure 8. Deflection Profile of Northlight Folded Plate

• Maximum stress of 33.601 kg/cm2 was obtained at node 2 from STAAD.Pro and when calculated manually a stress of 34.26 kg/cm2 was obtained at the corresponding node.(tension).
• Maximum stress of 97.789 kg/cm2 was obtained at node 3 from STAAD.Pro and when calculated manually a stress of 91.861 kg/cm2 was obtained at the corresponding node.(compression).
• Maximum stress of 85.539 kg/cm2 was obtained at node 4 from STAAD.Pro and when calculated manually a stress of 90.731 kg/cm2 was obtained at the corresponding node.(tension).
• Maximum nodal displacement of 0.183 mm was observed at node 10 in positive x-direction and a maximum nodal displacement of 10.321 mm was observed at node 101 in negative x-direction.
• Maximum nodal displacement of 0.102 mm was observed at node 101 in positive y-direction and a maximum nodal displacement of 7.187 mm was observed at node 108 in negative y-direction.
• Maximum nodal displacement of 0.901 mm was observed at nodes 210 and 10 in positive and negative zdirection.
• Maximum plate deflection of 36.9 mm was observed in plate 1 in manual analysis.
• A transverse moment of 113.840 kg-m was obtained at node 3 from STAAD.Pro and when calculated manually a moment of 539.597 kg-m was obtained at the corresponding node.
• A transverse moment of 1835.675 kg-m was obtained at node 4 from STAAD.Pro and when calculated manually a moment of 491.896 kg-m was obtained at the corresponding node.
• It was observed that the value of stress obtained from STAAD.Pro at node 2 was 1.92% less than the manually calculated stress at the corresponding node.
• It was observed that the value of stress obtained from STAAD.Pro at node 3 was 6.45% more than the manually calculated stress at the corresponding node.
• It was observed that the value of stress obtained from STAAD.Pro at node 4 was 5.72% less than the manually calculated stress at the corresponding node.
• It was observed that, in manual analysis the maximum stresses in plates can be compared with the STAAD.Pro output.
• Plate deflections were not obtained in the STAAD.Pro package, whereas, they can be calculated manually.
• Nodal displacements were obtained in the STAAD.Pro, whereas, they cannot be calculated manually.
• It was observed that the value of transverse moment obtained from STAAD.Pro at node 3 was 78.90% more than the manually calculated moment at the corresponding node.
• It was observed that the value of transverse moment obtained from STAAD.Pro at node 4 was 273.18% more than the manually calculated moment at the corresponding node.

8.1 Actual transverse moments

8.2 Longitudinal stresses

Longitudinal stresses are obtained by multiplying the fiber stresses obtained with a factor

• The value of stress obtained from STAAD.Pro at node 2 is less than the manually calculated stress at the corresponding node 3.
• The value of stress obtained from STAAD.Pro at node 3 is more than the manually calculated stress at the corresponding node 4.
• The value of stress obtained from STAAD.Pro at node 4 is less than the manually calculated stress at the corresponding node 5.
• The transverse moments calculated manually were conservative when compared to STAAD.Pro results.
• Maximum nodal displacements of 0.183 mm, 0.102 mm and 0.901 mm occurred at nodes 10, 101, 210 respectively in positive x, y and z directions.
• Maximum nodal displacements of 10.321 mm, 7.187 mm and 0.901 mm occurred at nodes 101, 108, 10 respectively in negative x, y and z directions.

• The static analysis was performed for the northlight folded plate roof in the present study. Further work can be carried out to obtain more accurate values when compared to the manually obtained results.
• Wind load analysis for different basic wind speeds can be performed for the northlight folded plate roof in the further work.