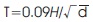
Fundamental period of vibration is determined by an empirical equation by many building codes. Many times these values are estimated over-conservatively. Many researchers have attempted modification in these formulae with an aim of predicting the period of vibration as close to the reality. Soft computing technique of Genetic Programming (GP) is applied to arrive at the simple empirical equation for fundamental period of vibration. In the present study, GP models are developed using input parameters which represent mass, stiffness and geometry of the buildings directly or indirectly. Total number of 70 buildings are analyzed out of which, data set of 49 buildings are used to develop the models. The GP technique has given the equations of period of vibration, which are then modified as per the error obtained from the experimentation conducted on mild steel frames. Finally a simple expression for fundamental period of vibration is suggested, which is then verified from the data set found in the literature.
The mass, strength and stiffness of the structure affects the fundamental period of vibration. Many factors such as structural regularity, height of the building, dimensions of structural members, properties of in fill panel, axial load level, reinforcement ratio and extent of concrete cracking are significant in the behavior building subjected to dynamic loads (Crowley & Pinho, 2006). Most of the codes have recommended empirical equation in terms of the height and dimensions of the building. These equations vary with the structural system and building material.
The fundamental period of vibration required for the simplified design of reinforced concrete structures has been calculated for many years using a simplified formula relating the period to the height of the building and dimension of the building in the direction of seismic force. IS 1893 (Part1): 2016 has given following equation in determining fundamental period of vibration:
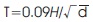
Where T is the fundamental period of vibration, H is the height of the building in meter and d is the base dimension of the building in the direction of the analysis. Sindel et al. (1996), concluded that ductile moment-resisting frames may not escape non-structural damage. They recommended the use of ductile shear walls (SWs) in almost all reinforced concrete (RC) buildings not only to provide adequate structural safety, but also to protect against non-structural damage. Sezen et al. (2003), found that buildings constructed using SWs as the primary lateral load-resisting system performed quite well in the 1999 Kocaeli, Turkey earthquake, and for the most part, buildings with SWs survived with limited or no damage. Sonuvar et al. (2004), have shown that the most effective and economic method of increasing the stiffness and lateral load strength of existing buildings is to add new elements such as a SW to the existing building system. Table 1 shows the summary of the empirical equations suggested by many building codes. As an alternative for buildings with concrete or masonry SWs, ICC (International Code Council, 1997) provides the following formula to compute Ct which depends on the properties of the SWs as follows:

Where,

Table 1. Empirical Equations of Period of Vibration Recommended by Different Codes (Kwon and Kim, 2010)
where Ai is the horizontal area (in square meters), Li is the dimension in the direction under consideration (in meters) of the ith SW in the first floor of the structure, and NW is the total number of SWs. The value of (Li/H) in Equation (3) should not exceed 0.9. Equation 5.3 took the following form:
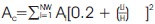
Crowley and Pinho (2010) stated that Equation (5) has an error and that Equation (3) is the original one; the difference may be due to an editing error, and the error should be rectified. Goel and Chopra (1998), calibrated using the measured periods of vibration of SW buildings and obtained the formula in Equation 5 which has been included in ASCE (2006) as follows:
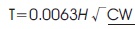
where the equivalent shear area is as follows:
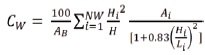
where AB is the building plan area, H is the building height in meters, Ai, Hi, and Li are the area in square meters and height and length in meters in the direction under consideration of the ith SW, and NW is the number of SWs. They also recommended that the period computed from a rational analysis should not exceed 1.4 times the value obtained from Equation 5. The lower limit of fundamental period represents the value measured under ambient vibration for the intact building with no cracks. However, the upper limit represents that obtained from strong motion records of the cracked building (Morales, 2000).Morales (2000), found that Equation 5 provided improved results as compared with any of the code suggested expressions, e.g., the Canadian code NBCC (National Building Code of Canada, 1996) or the American code, ICC (International Code Council, 1997). suggested that for French existing buildings, the fundamental period is proportional to building height or floor number. However, for design, they recommended relationships based on the wall lengths (Goel & Chopra, 1997). Crowley and Pinho (2010), suggested updating Equation 4 in the Eurocode 8 (CEN 2004) by the equation proposed by Goel and Chopra (1998). It is worth to mention that Equation 4 is valid for SW with different heights and takes into account shape factor and shear modulus, as well as both flexural and shear deformations. Gills and Mcclure (2008), performed ambient vibration measurements on 39 multi-storey buildings, ranging in height from 12 to 195 m, in Montréal, Québec (Canada). The dynamic properties of upto six vibration modes were then extracted from the measured ambient responses using the Enhanced Frequency Domain Decomposition (EFDD) method. The measured dynamic properties of the 27 RCSW buildings studied are compared to different models proposed in the literature. The empirical equations proposed in several building codes (National Building Code of Canada, 2005, ASCE/SEI 7-05, SEAOC,1999) to estimate the fundamental sway period do not fit the measured data very well. Based on the results of regression analyses, an improved equation is proposed as follows,

Where, T is the fundamental period of vibration and H is the height of the building in meter. Hatzigeorgiou and Kanapitsas, (2013), have proposed the following empirical equation where the flexibility of soil, the presence of in fill panels and concrete shear walls, the total height, and the width along the seismic direction have been taken into account.
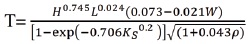
Where, L is the width of structure in seismic design direction under consideration (in meters) q is the ratio of the areas of shear wall sections along with a seismic action direction to the total area of the walls and columns. H is the height of the building in meters. Ks is the sub grade modulus of soil in mega Newton per cubic meter. W is identical with the amount of in fill panels which is 0 for bare frames and 1 for the buildings which have in fill walls in each moment resisting frames.
Lee et al. (2000), proposed improved formula for shear wall dominant buildings based on the full scale measurements on 50 apartment buildings in Korea.
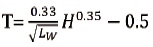
Where, Lw implies wall length in meters per unit plan area in square meters, T is the fundamental period of vibration and H is the height of the building in meters.
The difference between the real period of the building and the period obtained from the computer-based analysis using ETABS v6_13 is also presented and is shown by comparison that the ratio of measured periods to those obtained from the computer-based method is about 0.75 for the longitudinal direction and about 0.9 for the transverse direction.
Kwon and Kim (2010), suggested the following equation based on the data points of 56 RC shear wall buildings.
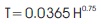
Morales (2000), suggested following equation for determination of period of vibration.
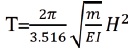
Where m is the mass of the building and H is the building height in meters.
To facilitate development of empirical equation of the fundamental period of vibration, data driven technique in the form of Genetic Programming (GP) is employed in the present studies. These data driven techniques extract the information from the data presented to them. Data- driven modeling can be considered as an approach to modeling that focuses on using the Machine Learning methods in building models that would complement or replace the “ knowledge-driven” models describing physical behavior(Solomatine,2002).
Section 2 of this paper describes the theory of GP along with its application in Civil Engineering. The generation of data required for the development of GP models, methodology and details of model formulation are discussed in Section 3. The results obtained through these models are shown in Section 4 and finally the conclusions are discussed in Section 5.
The concept of genetic programming (GP) is based on the evolution process that occurs in the nature where the species survive according to the principle of survival of the fittest'. GP provides the solution in the form of a computer program or an equation (Gaur & Deo, 2008). Although GP technique is used in the past in 1960s and1970s, GP emerged as a distinct discipline presented by Koza (Johari, et al., 2006).
A key advantage of GP over the other traditional modeling approaches is that it does not start with assuming an equation in any specified format. In at pical regression method, the model structure is specified initially and the coefficients are determined. For neural networks, the time consuming task of initially defining the network structure has to be under taken and then the weights are found by the learning algorithm. On the other hand, in GP, input and output parameters and set of functions are defined initially and the learning method subsequently finds both the optimal structure of the model and its coefficients. It is observed that handling of constants in the equation is trouble-some in case of GP. The selection of appropriate input parameters is extremely important in case of GP as well because any inappropriate input parameter may hamper the accuracy of the model.
Applications of Genetic Programming in Civil Engineering are sparse and few. Majority of them can be found in Hydraulic Engineering including wave hydro dynamics, Hydrology and Hydraulics. Londhe and Dixit (2012) have taken a comprehensive review of these applications along with theory of GP. Along with the applications in Civil Engineering, Heshmati et al. (2008), proposed new formulations for soil classification by means of Linear Genetic Programming (LGP). It was observed that LGP models were able to predict the target values to high degree of accuracy and the equations obtained through GP models were quite short, more simple and more practical as compared with then existing models found in the literature. Johari et al. (2006) employed GP to predict the Soil Water Characteristic Curve (SWCC) of soils. GP equations were compared with the experimental results as well as the models proposed by other investigators. This comparison indicated superior performance of the GP for predicting the SWCC. Shaw, et al. (2004) have discussed some basics of genetic programming and its applications in civil engineering and structural engineering.
Use of GP in Civil Engineering field is a very recent development. Joshi, et al. (2014) employed GP technique to determine fundamental period of vibration of moment resisting frames. No other references are noticed by the author in the field of application of Genetic Programming for seismic analysis of RC buildings although some applications are found in Hydraulic Engineering (Londhe & Dixit,2012).
The objectives of the present study is outlined as below:
The buildings are assumed to be fixed at the base without soil structure interaction and the floors as rigid diaphragm. The sections of the structural elements are rectangular for the beams as well as the columns. The thickness of slab is 150 mm and the height of the floor as 3 m or 3.5 m. The beam sections are considered at range of 230 mm x 450 mm to 450mm x 900 mm. The column sections for rectangular shapes are considered in the range of 230 mm x 450 mm to 1200 mm x 1500 mm. The length of shear wall ranges from 3 m to 5 m and thickness of shear wall ranges from 0.2 m to 0.35 m. The modulus of elasticity is considered as 5000ƒfck and the mass density as 25 KN/m3. The grades of concrete assumed in the analysis are M20 and M25. Length of the building is assumed between 25 m to 49 m, width of the building between 20 m to 30 m and height between 18 m to 90 m. Live load intensity is considered as either 2 KN/m2 or 3KN/m2. A typical floor plan of building is shown in Figure 1.
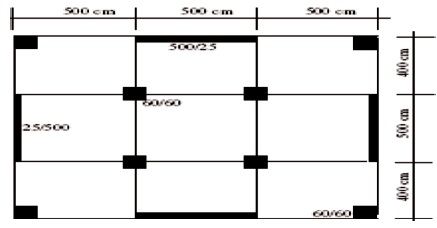
Figure 1. Typical Floor Plan
Total number of 70 buildings with height range between 6 storeys to 30 storeys is analyzed for natural periods of vibration along X as well as Y directions. The structures are assumed to be located in the seismic zone number III on the medium soil. Importance Factor (I) as 1 and Response Reduction factor (R) as 5 are considered for all buildings using ETABS. Effect of first three modes are considered for the dynamic analysis.
Out of the data for 70 buildings, the data set of 49 buildings is used to train the model and that of remaining 21 buildings is used to test the model. This division of the data is arrived after the several trials. So the division of the data is approximately 70 % for training and remaining 30% for testing the model. The statistic measures used to assess the accuracy of the developed models are Root Mean Squared Error (RMSE), Correlation Coefficient (R) and Coefficient of Efficiency (CE). A tree based GP has been employed to develop these models using GP Kernel Software developed by Babovic and Keijzer.
In the present study, Genetic Programming models are developed to predict the structural response in terms of natural periods of vibration along X and Y directions. GP1 category models estimates the natural period of vibrations for first three modes along X direction. GP2 category models estimates the natural period of vibrations for first three modes along Y direction. All GP models are developed with 8 input parameters. These input parameters are chosen considering the effect of geometry, mass distribution and the stiffness characteristics of the building frames in the dynamic analysis. Effect of geometry is incorporated in terms of L, W and H whereas the effect of the mass of the building is incorporated in terms of Wcmin, Wcmax, Dcmin, Dcmax and n. The stiffness characteristic of the building frames is assumed in terms of Wcmin, Wcmax, Dcmin, Dcmax and h. Table 2 and 3 shows the input parameters used along X and Y directions respectively.
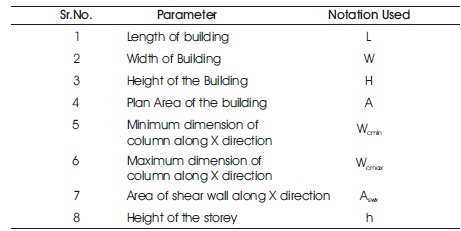
Table 2. Input Parameters for X Direction
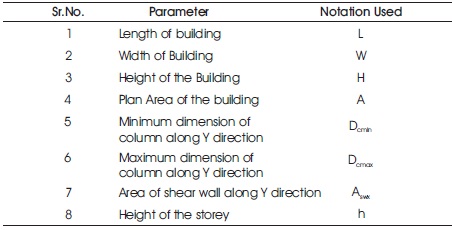
Table 3. Input Parameters for Y Direction
As per the discussions in previous paragraphs, GP models are developed and comparison of the results are discussed here in this section.
The hypothesis obtained from the developed GP models is as follows,
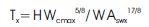

Upon substituting the values of Wcmax, Aswx, h and Dcmax, the equations are reduced to following forms:

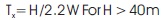
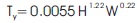
Mild steel frames are tested on Uni-axial shake table to determine the fundamental period of vibration (T1). Table 4 shows the details of the frames tested and the experimental results. The steel frames are tested along the Y direction. Figure 2 is the photograph of the frame, taken during the experimentation. Table 4 shows that the experimental value of (T) is found to be higher than analytical value by around 10.75%. It may be noted that even though the mild steel frames without shear walls are tested, the same percentage of error is incorporated in the Equation (16) and (17) .This is due to the fact that the aim of experimentation is to quantify the error in the period of vibration due to the assumptions made to simplify the analysis. However, IS 1893 (Part1):2016 has given the equation of period of vibration as shown in Equation (18).
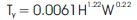


Figure 2. Photograph of Mild Steel Frame
The equations obtained are validated for the measured values of period of vibration along Y direction. The data set used in Table 5 is referred from Lee, et al. (2000). Table 5 indicates that the period of vibration values obtained through Equation (17) is closer to the measured period of vibration many a times than the values obtained using Equation (18). The ratio of predicted value using Equation (17) to the measured value varies from 0.95 to 1.19 except for three buildings. Table 6 shows the result of GP models For the performance parameters R, RMSE, and Ce5.
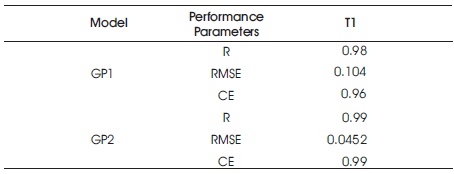
Table 6. Results of GP Models
The study has been carried out on symmetric buildings and the simplified equations are obtained using genetic programming. These equations may be used for symmetric buildings only. Furthermore, being a data driven tool, the inherent drawback of the study is the applicability of its outcomes that would be applicable for those input parameters which falls within the range of the values considered in the training data set used to derive the equations.