The review of literature had revealed that most of the existing approaches for describing the temporal variation of scour depth near a pier is an important aspect. It becomes pertinent to some laboratory and field cases for which the time factor plays a significant role. Important investigations on the time variation of scour have previously been carried out by Chabert and Engeldinger (1956), Ettema (1980), Kothyari (1990), Yanmaz et al. (1991), Melville and Coleman (2000) and others.

The studies that has been carried by the different investigators is mainly based on the dimensional analysis of different parameters describing the scour process by regression analysis of laboratory and field data, and thus giving the equation by drawing an envelope curve, and this results in overestimation. But majority of the investigators have used the dimensional analysis approach.

The process of local scour can occur in one of the two ways: (i) clear-water scour; and (ii) live bed scour. Clearwater scour occurs when the bed material upstream of the scour area is at rest i.e. there is no sediment supply into the scour hole by the upstream flow. The bed shear stresses away from the scour area are thus equal to or less than the critical or threshold shear stress for the initiation of particle movement. Live-bed scour, also referred to as scour with sediment transport, occurs when there is general bed load transport by the stream i.e. in this type of scour process, the sediment carried by the upstream flow is continuously supplied into the scour hole.

From Figure 1, it can be observed that the scour depth is variable with time, and it increases with increase in time. Also clear-water scour is higher than live-bed scour. Hence in present case, temporal variation of clear-water scour at cylindrical bridge pier has been studied.

Figure 1. Pier Scour Depth in a Sand-bed Stream as a Function of Time.(Raudkivi and Ettema 1983)

Thus in this paper, mainly prediction of temporal variation of clear-water local scour at bridge piers based on dimensional analysis of parameters describing scour depth has been discussed. Variation of the maximum scour depth for the laboratory data for clear-water including 100 hours data of different investigators with the parameter, involving size of the piers, flow and sediment characteristics has been presented.

The mechanism of local scour is a very complex threedimensional separation due to large variations in the flow field conditions from one site to another, moreover, numerous variables describing the flow, the fluid, the sediment characteristics, the channel and the obstruction geometry etc. The mechanism associated with the problem of local scouring have been studied for more than six decades. The investigators have pointed out that the vortex systems are the basic mechanism of local scouring, since many experimental works exist on the problem of local scouring. However, in most of these studies, emphasis has been on the formulation of scour depth equations, rather than modelling the problem of local scouring. A summary of important experiments on local scouring has been given by Chabert and Engeldinger (1956), Melville (1975), Breusers et al. (1977),Melville and Raudkivi (1977), Dargahi (1982), Chang (1988), Dey (1997), Graf and Istiarto (2002) and others.

The basic mechanism causing local scour at piers is the down-flow at the upstream face of the pier and formation of vortices at the base. The flow decelerates as it approaches the pier coming to rest at the pier face. The approach flow velocity is reduced to zero at the upstream side of the pier, which results in a pressure increase at the pier face. The associated pressures are highest near the surface, where the deceleration is greatest, and decrease downwards. Since the velocity is decreasing from the surface to the bed, the pressure on the face of the pier also decreases accordingly forming a downward pressure gradient. The pressure gradient hence forces the flow down the face of the pier, resembling that of a vertical jet. The resulting downflow impinges on the streambed and creates a hole in the vicinity of the pier base. The downflow impinging on the bed is the main scouring agent. Figure 2 shows the flow and scour pattern at a circular pier.

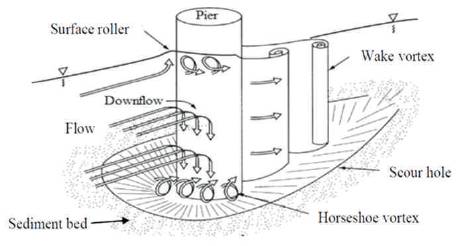
Figure 2. Flow Pattern and Mechanism of Scouring around Bridge Pier

The following factors that affect the local scour depth around piers and abutments are (i) velocity of the approach flow, (ii) depth of flow, (iii) width of the pier, (iv) length of the cylindrical bridge pier if skewed to flow, (v) size and gradation of bed material, (vi) angle of attack to a pier or abutment, (vii) shape of a pier or abutment, (viii) bed configuration, and (ix) ice formation or jams and debris which is not a factor in the present study. These factors have been discussed in the following sections.

The relation between the depths of local scour at a bridge pier D_s and its dependent parameters can be written as

(1)

where ρ and v = fluid density and kinematic viscosity, respectively; U = mean approach flow velocity; H = mean approach flow depth; g = acceleration of gravity; d₅₀ and σ_g= median size and geometric standard deviation of the sediment particle size distribution; ρ_s= sediment density; D = pier width; t = time; and f denotes “a function of.”and ρ, ρ_s, U, d₅₀ , D, H, g parameters may be also replaced by the following ones.

(2)

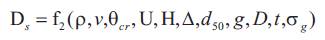
where,Δ =(ρ_s - ρ) / ρ, the relative submerged density and θ_Cr is Shields' sediment grain entrainment parameter i.e. θ_Cr = U²_*c / Δgd₅₀ and U_*c is the critical shear velocity at which sediment grain starts moving.

Scour involves three fundamental dimensions i.e. mass, length and time. The eleven independent variables (Eq. 1) are reducible to a set of eight non-dimensional parameters by the Vaschy-Buckingham-theorem. We can also write Eq. (2) in a non-dimensional form as:

(3)

For the flow conditions in the present study, the general statement can be simplified by the following assumptions:

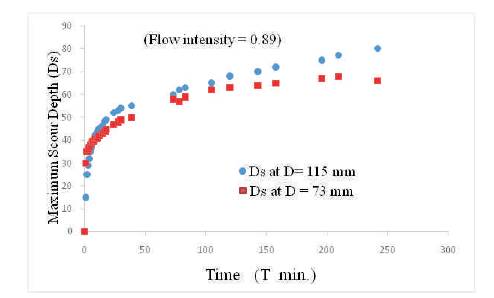
Figure 3. Maximum Scour Depth Vs. Time (D= 115 and 73 mm)

• The value of D_s /D is the most convenient basic relationship to express local scour depth. Experiments clearly indicate that if time effects are discounted by confirming attention to the final or equilibrium scour depth, D_se , and if the flow is strong enough to produce active scouring, then the ratio D_s/D is relatively insensitive to other factors and usually falls within the range of 1.0 to 3.0. As many authors suggest that the depth of scour is determined primarily by the horseshoe vortex, the dimensions are closely related to the pier width and thus scour depth.
• The term, U²_*c / Δgd₅₀ is a well-known Shields' entrainment parameter (θ_cr) for the beginning of bed movement. It expresses basically the power of the flow to initiate bed material movement and hence scour. As has been shown by several investigators, the state of bed mobility and transport affects greatly the nature of the scour depth versus time curve (Figure 3) and to a lesser extent affects the final or equilibrium scour depth.
• The variation of flow intensity on the temporal development of local scour was also considered. For the analysis of the effect of the cylindrical bridge pier diameter on the temporal development of the maximum scour depth, in first test, the pier diameter used was 115mm while in the second test, the diameter of the pier was 73mm. Figure 3 shows the temporal development of the maximum scour depth. As the results show, greater depth of maximum scour occurred for the larger diameter pier (D=115mm) when compared with the smaller pier of diameter 73mm. Also, the scour depth increased with time for each case. Thus, smaller the size of the pier, the longer it takes to reach a given value of the scourdepth. The same observation was made by Ettema (1980).
• The term, d₅₀ /H, is necessary in order to define the vertical velocity profile and the bed shear stress, for the given mean velocity of flow.
• The term, D/d₅₀ , is the pier diameter relative to sediment mean size, termed the sediment coarseness. For uniform sediments, local scour depths are unaffected by sediment size unless the sediment is relatively coarse. Laboratory data shows that the local scour depth is influenced by sediment size when D/d₅₀ <50. For local scour at piers,Ettema  (1980) defined that as the larger value of the coarseness sediment ratio is individual, grains are relative to groove excavated by the downflow, and erosion is impended because the porous bed dissipates some of the energy of the downflow. The scour is said to occur in coarse sediment in such cases.
• The term, Ud₅₀ /v, is a form of grain Reynolds number. In the case of small or light grains, it is required in order to specify the state of bed transport and the susceptibility of the bed to local scour. In the case of large or heavy grains, it may be possible to neglect it.
• The term, H/D, is a necessary geometrical ratio expressed in part, the geometry of the horse-shoe vortex system. Its influence on D_s/D has been clearly s demonstrated by experiments. H/D ratio is also useful for describing the interaction of the down flow into the scour hole, the horse-shoe vortex at the base of the pier, and the counter-rotating water surface roller near the top of the pier. For small values of H/D, the surface roller interacts with the down flow into the scour hole.
• The term, Ut/D expresses similarity in the time development of scour. It may be eliminated if attention is confined to the final or equilibrium scour depth, D_se . But time to reach equilibrium is large which is very difficult to measure in the laboratory. So to establish relationship for scour depth for any time, t, it is an important parameter.
• The term, U²/gd [i.e.IF = U/(gD)^0.50, defined as pier Reynolds number] can be also expressed as H_s/D which is the ratio of the stagnation pressure (H_s ) at the leading edge of the pier, U²/2g, normalized with pier diameter, D. The parameter U²/gD is, therefore, useful for describing flow gradients around a pier; for the same stagnation head, U²/2g, steeper flow gradients occur with smaller values of pier diameter, D.
• Bed material properties do not change, thus the geometric standard deviation of particle size distribution is constant (σ_g). Ettema (1976, 1980) and Wong (1982) andKothyari (1990) carried out systematic laboratory studies of the effects of sediment nonuniformity on local scour depth under clear-water conditions at cylindrical bridge piers.

In the present study, D/d₅₀ and clear-water flow condition have been considered. Also the effect of sediment size has been considered in Shields' entrainment parameter θ_cr= U²_*c/ Δgd₅₀ . Thus the non- dimensional parameters d₅₀ / H, D/d₅₀, Ud ₅₀/ υ can be dropped out.

Thus from the above discussion following nondimensional parameters describing the equilibrium scour depth around circular bridge piers at any time, t has been found to be important and can be written as;

(4)

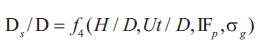
Raudkivi and Ettema (1983) and ShriRam and Pande B.B (1997)derived an equation for estimating the maximum depth of local scour at circular piers based on laboratory experiments for cohesionless bed sediment. They concluded that the equilibrium depth of local scour (D_se) decreased as the geometric standard deviation of sediment (σ_g) increased (an exception occurs when σ_g < 1.4. Also observed by Pagliara (2007), in the case of a non-uniform material, i.e., σ_g < 1.4, the scour is less compared with that of a uniform material with the same median particle size (d₅₀).

Figure 4 shows that the Scour depth is dependant on geometric standard deviation of sediment (σ_g), as the geometric standard deviation of a sediment mixture increases, the rate of scour decreases the quantitative relationships for the effect of geometric sediment gradation. They concluded that the equilibrium depth of local scour decreased as the geometric standard deviation of sediment increased.

(5)

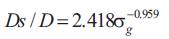
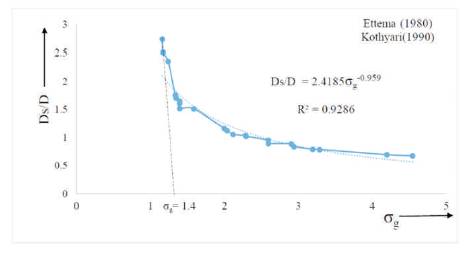
Figure 4. Variation of Non-dimensional Scour Depth (D_s /D) Vs. σ_g

Analysing the result of fine sand (d₅₀ = 0.16mm) for Figure 5, 100 hours flow duration, the curve of relative scour depth Ds/D versus non-dimensioned time (Ut/D) for different diameter of cylindrical piers are drawn and is shown in Figure 6. It may be observed that the scour depth increases with increasing time, in general.

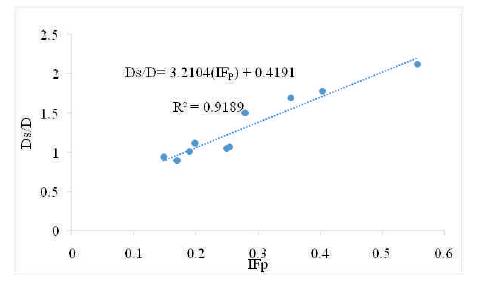
Figure 5. Variation of Non-dimensional Scour Depth Vs. Pier's Froude Number

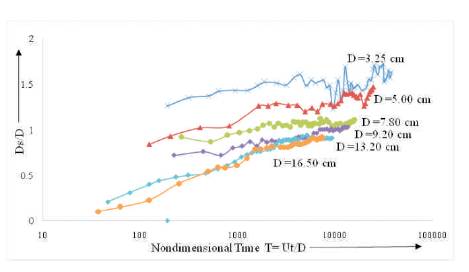
Figure 6. Temporal Variation of Scour Depth Vs. Time

From Figure 7, following equation for scour depth is obtained.

(6)

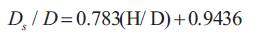
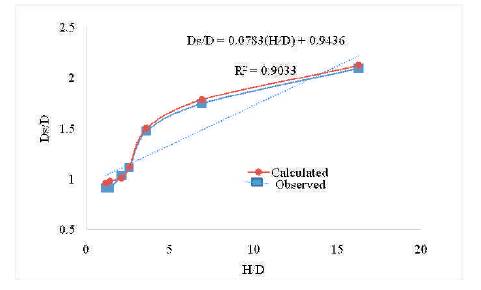
Figure 7. Variation of Non-dimensional Scour Depth Vs. (H/D) in uniform sediment

As an initial attempt to correlate scour depth with time, a curve obtained from regression analysis in functional form-

(7)

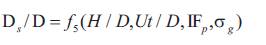
And draping σ_g for uniform sediments i.e.

(8)

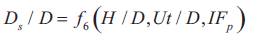
and is plotted in Figure 8. This figure shows that the scour depth is tending to reach equilibrium at long hours of run, also the relationship shows that scour depth varies with time in logarithmic scale in the mid-range.

Figure 8 can be given as the following equation i.e.

(9)

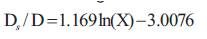
where

 

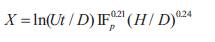
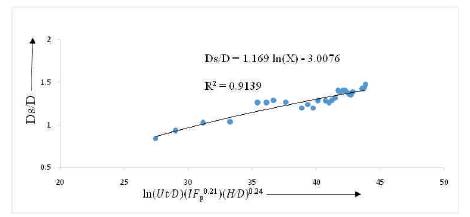
Figure 8. Prediction of Scour Depth as a Function of Time

In the initial and at the final stages, the scour depth follows nonlinear pattern with logarithmic time as variable. This leads to observe the rate of scour as a function of time.

This study is limited to local scouring at cylindrical bridgepiers in uniform and non-uniform sand beds. The following conclusions can be drawn from this study:

(10)

(11)

(12)

(13)

• Scour depth is variable with time and it increases as time increases for the same incoming flow conditions.
• Scour depth increases with increase in pier's Froude number (IF_p ) i.e.
• As scour depth is dependent on geometric standard deviation of sediment (σ_g), they concluded that the equilibrium depth of local scour decreased as the geometric standard deviation of sediment increased i.e.
• Scour depth is also dependent on (H/D) ratio, it increases with increase in (H/D) ratio i.e.
• Prediction of Scour Depth as a Function of Time, scour depth varies with time in logarithmic scale in the midrange and it can be given as the following equation i.e.

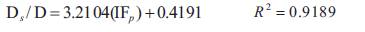
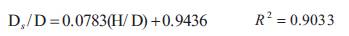
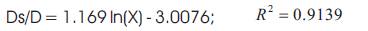
where,

 

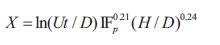
By putting the value of X in above equation, the equation for clear-water local scour depth prediction is achieved.

The following symbols are used in this paper

D = pier diameter (m) ;

D_s= scour depth (m) ;

D_se = equilibrium scour depth (m) ;

d₅₀= median sediment size (m) ;

f = arbitrary function;

g = acceleration due to gravity (m/s²) ;

H = water depth (m) ;

H_s= water depth used to reach the scour depth (m) ;

t = time (s) ;

U = mean approach flow velocity (m/s);

υ= water kinematic viscosity (m²/s) ;

ρ = water density (kg/m³) ;

ρ_s= sediment density (kg/m³) ;

σ_g= geometric standard deviation (-)

IF_p= pier Froude number of approach flow (-);

Δ= relative submerged density ( ρ_s-ρ) / ρ;

θ_cr= Shields' sediment grain entrainment parameter, θ_cr= U²_*c / Δgd₅₀

U_*C = critical shear velocity at which sediment grain starts moving.