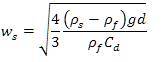
The settling velocity of the particle is an important parameter in the area dealing with sedimentation engineering, chemical engineering and environmental engineering. A lot of work has been done by researchers on the determination of expressing settling velocity relation, and as a result lots of relations had come to existence. The major disadvantage with relation is that they cannot come to implant in engineering applications, as most of them hold one or other limitations. In this work, a settling velocity relation has been proposed which is applicable to all ranges of Reynolds number.
The settling velocity of the particle is the resultant downward velocity which comes into existence when acceleration of particle falling is zero. The proper definition is as settling velocity of a particle is downward, velocity at equilibrium in which the sum of gravity force, buoyancy force and drag force is equal to zero. Settling velocity depends on both the properties of the fluid as well as properties of the particle. It means it depends on density and viscosity of the fluid, and the density, size, shape, surface texture of the particle.Many attempts to predict the particle settling velocity have been undertaken in literature, starting with Stokes in 1851[cited as Graf 1971] and followed by Oseen (1927), Rubey (1933), Rouse (1938), Sha(1954), Interagency committee (1957), Turian (1971), Zanke (1977), Yalin (1977), Clift(1978), Zigrang and Sylvester(1981), Hallermier (1981), Dietrich (1982), Turton and Clark (1986), Khan and Richardson(1987), Zhang(1989), Van Rijn (1989), Swamee and Ojha (1991), Wilson et al (1992), Concharov [citied in Ibad-zadeh 1992], Schiller (1992), Zhu and Cheng (1993), Hartman (1994), Julien (1995), Cheng (1997), Soulsby(1997), Ahrens (2000), Chang and Liou Formula(2001), Jimenez and Madsen (2003), Brown and Lawler (2003), Wu and Wang (2006), Almedeij(2008), Cheng and Nian-Sheng (2009), among others, who all developed equations for determining settling velocity.
To estimate the settling velocity of particles, two different approaches can be followed: (1) an idealized one in which the particle is assumed sphere and (2) a more realistic one in which the particle shape is considered. In this study, both of the two approaches has been dealt, which considers shape of the factor and the resultant diameter.
Settling velocity of the particle is downward velocity at equilibrium, in which sum of gravity force, buoyancy force and drag force, equal to zero. i.e. fg + fb + fd = 0, noting into vector terms this relation modifies to fg - fb - fd = 0. From this relation settling velocity is derived as
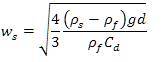
Determination of drag coefficient can be determined by the relation provided.
The value of the coefficient of drag coefficient varies with the flow regimes of laminar, transitional, and turbulent flows.

Determination of settling mostly depends on the curve between drag coefficient and Reynolds number. The major problem with the method is the particle characteristics affects the relation between drag coefficient and Reynolds number. Many equations have been developed which consist of work being done by Rubey (1933), Interagency committee (1957), Zanke (1977), Hallermier (1981), Sha(1954), Julien (1995), Cheng (1997), and Ahrens (2000, 2003) for settling velocity of the particle.
Cheng(1997) illustrated relationship between Cd and Re which takes a similar form in many semi empirical equations for drag coefficient. Its basis is the asymptotic behavior of both settling velocity and Reynolds number. This conclusion leads to the formation of expression in terms of dimensionless parameter. The process was being described by Camenen(2007), and is outlined as below:
Cd and Re are related as such
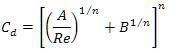
Where, n, A and B are constants. The dimensionless diameter is defined as
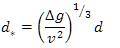
The drag coefficient relation coined by Newton in terms of settling velocity is as
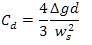
There are two asymptotic equations of the settling velocity depending on Reynolds number,.i.e.Cd = A/Re, when Re < 1 (Stokes flow), and Cd =B when 105 < Re < 2 X 105 (turbulent flow), where A and B are constants. A relationship for stokes flow condition is determined as:
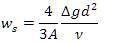
In a similar way, for the case of turbulent flow condition settling velocity can be expressed as:
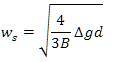
Drag coefficient can be expressed in terms of dimensionless diameter by combing equations (4) and (5) as:
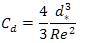
Finally, settling velocity can be calculated by equating equation (3) and (8) in terms of settling velocity as:
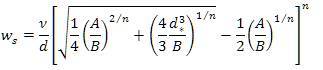
Different researchers have equated different values for the coefficients A,B, and n for the spherical particles and natural particles, which are being listed in Table 1.

Table 1. A,B, and n for the spherical particles and natural particles given by different Investigators
Camenon(1997) proposed three equations , one for each coefficients in equation (9), that took into notice of paramters like shape, size and densities. But as per Wu(2008), this was not practically applicable for determination of settling velocity. Therefore Wu(2008) proposed a new relation combining 3and 4 as:
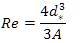
As, per Cheng(1997), he analyzed data of Concharav (1962), Zegzhda(1934), Arkhangel'skii(1935) and Sarkisyan (1958), and proposed the relation 3 as for the value of n=1.5 as:
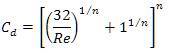
Substituting equation (8) into equation (11), a new modified relation can be obtained as
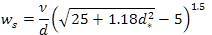
Equation [4] can be modified as:
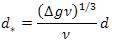
Expressing equation (13) in terms of form and modifying equation (12) as:
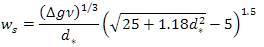
This equation can be further modified as:
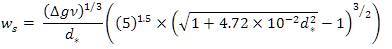
or,

Dimensionless settling velocity parameter is defined as:
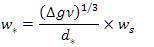
The proposed settling velocity in terms of dimensionless parameter is as:
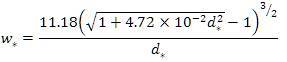
Where, dimensionless settling velocity and diameter is being defined in equation (4) and (17).

Eighteen equations have been used for computing of the comparisons, as listed in Table 2, selected from literature. All the equations have been considered for all regime flow conditions. The results and comparisons have been tabled in Table 3 and Table 4 and relative results have been illustrated in Figures 1, 2 and 3.The proposed equation has been matched with the experimental data and data available in literature. The relative percentage error and rms with the proposed equation is far much better as compared with other equations available in literature.

Table 3. Relative error with different investigators
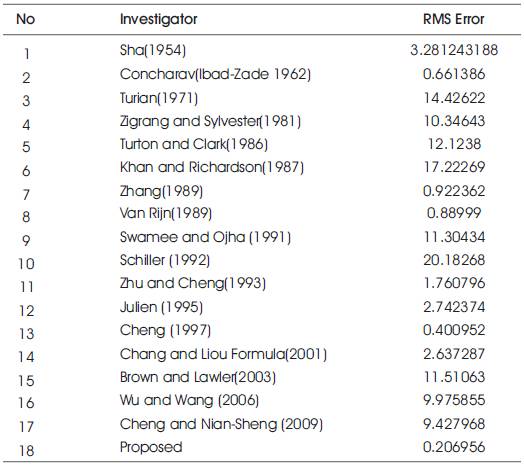
Table 4. RMS error with different investigators
Despite of its simple form, the equation proposed here is valid for all ranges of Reynolds number, which has been validated for the data available in literature as well as data of experiment performed. The settling equation proposed here is of dimensionless terms, and this makes easier to evaluate the settling velocity of the particle. The equation proposed gives a relative percentage and rms error of 2% and 0.21% which can be said to be under permissible limits.
Settling Velocity equation proposed is valid for Reynolds number which is valid for all regime flow. This equation is in simplified form and can be used in common application for designing of settling basins.
The following symbols are used in this paper
| Cd | = | drag coefficient; |
| d | = | diameter of a particle; |
| de | = | dimensionless particle parameter; |
| g | = | gravitational acceleration; |
| Re | = | particle Reynolds number; |
| T | = | Temperature |
| Ws | = | settling velocity of particle; |
| α | = | parameter; |
| Δ | = | (ρs-ρ) /ρ; |
| ν | = | kinematic viscosity of fluid; |
| ρf | = | density of fluid; |
| ρs | = | density of particles; |