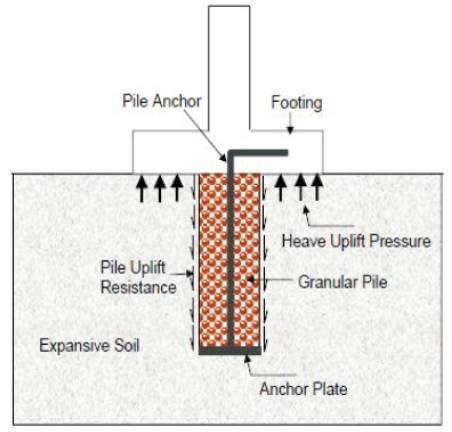
Figure 1. Typical granular anchor pile foundation system (Ismail 2011)
Ground improvement refers to a technique that improves the engineering properties of the soil like shear strength, stiffness and permeability. Stone column is one of the ground improvement techniques often applied due to its low cost, environment friendliness and ease in construction. Stone columns are employed to resist the compressive loads. They are not capable to resist uplift pressure. Stone column modified with anchor at the base of the stone columns refered to as Anchored Stone Column (ASC). ASC can resist uplift pressure in addition to compressive load. An anchor placed at the base of the stone column and attached to the footing by a cable or rod, transfers the applied force to the bottom of the stone column. This paper demonstrates the result from two dimensional finite element analysis using PLAXIS 2D software, under taken on a typical unit cell model. The study will investigate the ability of ASC to resist uplift force and failure modes. The parametric study considers the effect of length to diameter ratio of stone column, area replacement ratio, stiffness of the stone column material to that of soil surrounding the stone column.
Due to rapid urbanization, and socio-economical aspects, construction is carried out on soils which are left in the past. These soils include soft clays, loose sand, filled up soil, etc (Tandel et al. 2014). Stone column is the one of the ground improvement techniques widely used for various flexible and rigid foundations. Structure constructed on expansive soils, are often subjected to uplift pressure due to swelling pressure imparted by these soils. Stone columns are not liable to sustain this uplift pressure. Recently Anchored Stone Column (ASC) also called Granular Anchor Pile technique was developed to resist the uplift pressure.
Granular Anchor Pile (GAP) is capable of providing resistances against compressive and pullout loads in addition to ground improvement. It is relatively a new concept that extends the functional utility of granular piles to withstand uplift loads also. An anchor placed at the base of the granular pile and attached to the footing by a cable or rod transfers the applied pullout force to the bottom of the granular pile. Figure 1 shows the basic Granular anchor system.

Figure 1. Typical granular anchor pile foundation system (Ismail 2011)
Many researchers have reported numerical analyses of ASC. Ismail (2011) carried out three dimensional finite element analyses using commercial software PLAXIS 3D software, undertaken on a typical double-story building constructed over a system of granular anchor pile foundation system in a reactive soil. Both heave and shrinkage were modeled by applying equivalent volumetric strains to the affected area. He concluded that the maximum vertical displacement is totally resisted by the ASC technique, and no heave induced vertical displacement was produced. It was also concluded that the ASC technique reduced the maximum angular distortion of the top beams dramatically. Vidyaranya et al. (2008) conducted non-linear analysis of displacements of granular pile anchors in Homogeneous ground. The elastoplastic response of the GAP installed in a homogeneous ground is analyzed with the shear stresses at the interface limited to the undrained strength of the soil.
They addressed that long GAP is more effective in transferring applied loads. In addition to this, they added that the GAP behaves like an incompressible or a rigid pile for relative stiffness factor more than 1000. Sawant et al. (2010) proposed equation for displacement and stresses in non-dimensional form for anchored stone column. They observed that with increase in length to diameter ratio, displacement at the bottom of the stone column decreases and optimum length of the stone column was observed to be about 10 times the diameter of stone column. They also showed that the displacement decreases with increase in modules of stone column material. Based on the laboratory model test results, Rao and Padmavathi (2010) carried out multiple linear regression analyses and proposed an equation for swelling potential of the expansive soil, reinforced with granular pileanchors.
Numerous researchers carried out laboratory and field load tests on anchored stone column. Hari Krishna and Murthy (2013) made comparison of pull out resistance of concrete pile and granular anchored column through filed load tests. They argued that pull-out resistance of the granular anchor column is around 3 to 4 times that of similar concrete piles. For the same surface area, the effect of diameter on the pull-out capacity is more than that of length in increasing the pull-out resistance. Phanikumar et al. (2004) conducted laboratory model tests on anchored granular column embedded in expansive clay beds. They revealed that the heave of the expansive clay beds was reduced by about 96%. It was also observed that the undrained strength of the clay surrounding the 3 granular pile anchor improved by about 20%. For two-group columns, minimum heave was observed when the spacing between the granular pile anchors was kept at twice the pile diameter. The uplift resistance increases with increase in diameter and the relative density of the granular column material. Phanikumar et al. (2008) conducted field load tests on anchored granular columns to check their performance in expansive clayey soil. The parametric study was undertaken to study the rate of heave, reduction of heave and variation of heave with radial distance and with depth. It was found that heave was reduced by about 90% upon installation of granular pile-anchors. Final heave was reached in just about half the time required for final heave in the case of an unreinforced expansive clay bed. Hari Krishna et al. (2013) compared the behaviour of granular anchor piles and cushions found on expansive clay bed through field load tests. The tests were conducted on three flooring panels of 3m×3m size cast in the field with different treatment alternatives and their cyclic swell-shrink movements were monitored for four years. Their study revealed that heave was decreased by 26% and 92% for cushioned flooring panel and cushion-cum- anchored granular piled flooring panel, respectively. Through the laboratory model tests, Aljorany et al. (2014) studied the influence of different parameters, such as GAP length (L) and diameter (D), footing diameter (B), expansive clay layer thickness (H) and presence of non-expansive clay. Their results indicated that the heave can be reduced with increasing length and diameter of GAP. They also argued that the heave can be reduced by up to (38 %) when GAP is embedded in expansive soil layer at (L/H = 1) and reduced by about (90 %) when GAP is embedded in expansive soil and extended to non-expansive clay (stable zone) at (L/H = 2) at the same diameter of GAP and footing. Rao et al. (2007)conducted field load tests to check the pull out resistance of the GAP seated in expansive clay bed. Based on their study, it was observed that the GAP of larger surface area resulted in higher pullout capacity. In addition to this, it was also argued that when the length of the GAP was increased from 500 to 750 and 1000 mm, the percentage increase in the uplift load required for an upward movement of 25 mm was 33.3 and 55.5% respectively.
Although the behaviour of anchored stone column is being studied in the field and laboratory, there is a need of proper investigation of the performance of anchored stone column by finite element modelling. This paper addresses the parametric study of anchored stone column performed by two dimensional finite element software PLAXIS 2D. Typical parameters include cohesion of soft clay, friction angle of stone column material, length of stone column, diameter of stone column and stiffness of geosynthetic. The results are presented in the form of loadsettlement and bulging of stone column along the depth of stone column.
Anchored stone column geometry for benchmark case is schematically shown in Figure 2. An Axi-symmetry model condition was considered for two dimensional finite element analyses. In the analyses, spacing of ASC, 4 stone column diameter, cohesion of soft clay, frictional angle of stone column material are varied as summarized in Table 1. The parameters for benchmark case are mentioned in Table 2. The properties of stone column and soft clay were selected in the range of their typical range to leave enough margins for the variations in the parametric study (EPRI 1990).Recently, geosynthetic reinforced stone column technique was developed to employ in very soft soil for improving the performance of ordinary stone column. In this paper geosynthetic stiffness is one of the parameter varied for the parametric study. The geosynthetic stiffness is defined as the ratio of tensile force per unit width of the average strain in the geosynthetic. The zone of interface stone column and soft clay, stone column and geosynthetic were neglected for simplification.
As seen in Figure 2, stone column with anchor rod and anchor plate is constructed in soft clay with 1 m stiff clay at the bottom to represent the rigid layer. To eliminate the boundary condition, width and depth of the model was taken equal to 10 times and 8 times the diameter of the stone column, respectively.
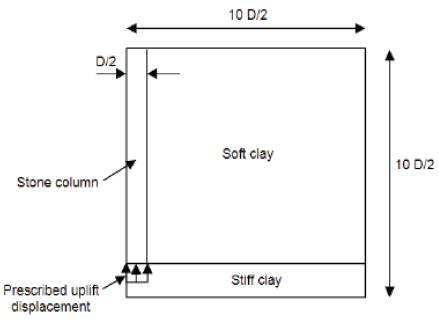
Figure 2. Schematic diagram of anchored stone column embedded in soft soil
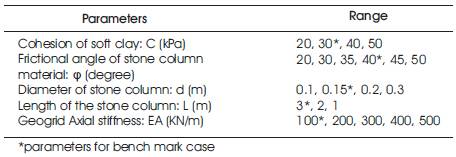
Table 1. Parameters varied
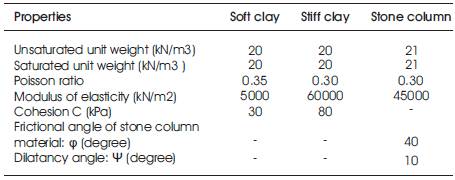
Table 2. Properties of different materials for benchmark case
An axi-symmetrical model was developed to study the performance of anchored stone column. The FE package PLAXIS 2D was used for the FE modelling. Typical model is shown in Figure 3. The model consists of 920 elements. The mesh was refined in the region of the 5 column-soil interface to increase the accuracy of the predictions.
As the displacement boundary is concerned, bottom boundary is fixed in vertical and horizontal direction. The left and right vertical boundary is allowed to settle in vertical direction only. The finite element mesh was developed using 15 nodded triangle elements to represent soft clay and stone column. The geosynthetic was modeled as geogrid element available in PLAXIS 2D. Finer mesh arrangements were used for all the analyses to achieve greater accuracy. Mohr-Coulomb failure criterion was adopted for stone column, soft clay and stiff clay having linear elastic perfectly plastic behaviour. The geosynthetic has axial stiffness only.
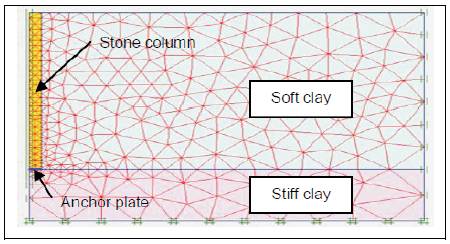
Figure 3. Finite element modelling of anchored stone column
Figure 4 indicates the effect of cohesion of soft clay on uplift force-displacement behaviour of anchored stone column of 3 m length and angle of internal friction of stone column equal to 40˚. From this figure it can be seen that with increase in cohesion, uplift resistance of stone column increases. For instant, for a given displacement of 50 mm, as cohesion changes from 20 to 50 Kpa, uplift force increases by 13%. This may be due to increase in the amount of confinement pressure provided by the surrounding soil with increase in cohesion.
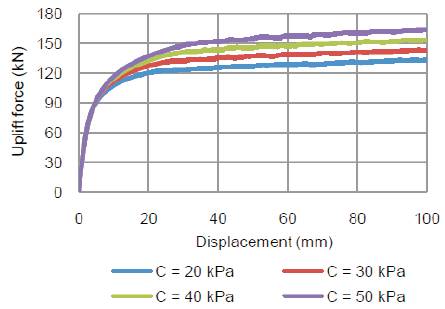
Figure 4. Uplift force Vs. Displacement for different cohesion of soft clay
The bulging (or lateral deformation) developed along with the length of anchored stone column is illustrated in Figure 5. It can be seen that with increased in depth of stone column, bulging of stone column increases and attained a maximum near the bottom portion of stone column. This depth from the bottom of the stone column is 0.097 m i.e. 1.5 times of diameter of the stone column. The decrease in bulging with increase in cohesion may be thought due to the increase in amount of lateral pressure provided by clay.
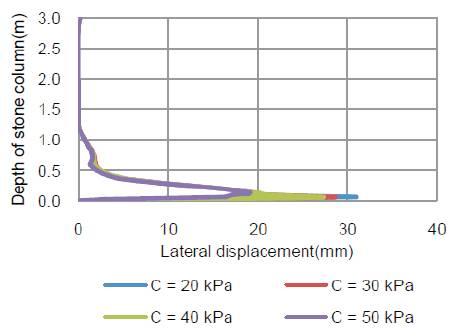
Figure 5. Effect of cohesion of soft clay on lateral displacement of stone column
Effect of angle of internal friction on uplift forcedisplacement behaviour of stone column is shown in Figure 6. It can be seen that with increase in friction angle of stone column material, uplift force increases for all values of angle of internal friction. For instance, for given settlement of 50 mm, as friction angle increases from 30 to 50˚, uplift force increases by about 11%. This may be due to increase in the amount of lateral resistance offered for greater friction angle of stone column material.
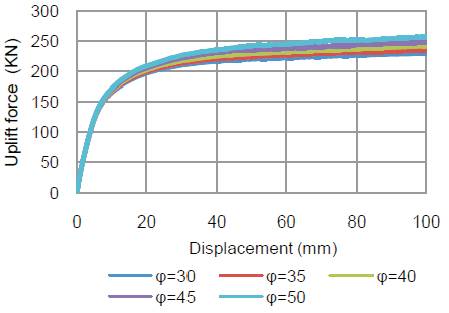
Figure 6. Uplift force Vs. Displacement for different frictional angle of stone column material
Figure 7 illustrates the lateral deformation developed along the length of stone column. This figure clearly indicates that the maximum bulging occurs near the bottom portion of stone column. This depth from the bottom of the stone column is about 0.8 times the diameter of the stone column. The decrease in bulging with increase in internal friction of stone column material may be due to higher lateral resistance pressure by the stone column.
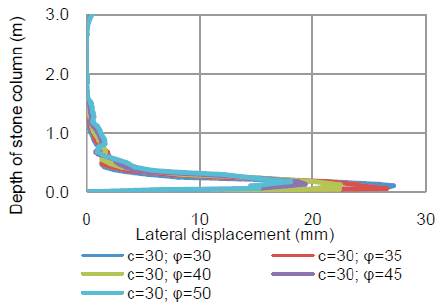
Figure 7. Effect of frictional angle of stone column material on lateral displacement of stone column
Figure 8 illustrates the uplift force-deformation response of anchored stone column for different diameter of stone column. It is clearly seen that the uplift force increases remarkably with increase in diameter of stone column. This phenomenon may be due to higher shaft resistance with increase in diameter of anchored stone column. From Figure 8, it can be said that as diameter of anchored stone column increases from 0.2 to 0.3 m; uplift force increases from 275.04 to 575.44 kN. This also indicates that uplift force capacity of 0.3 m diameter column is two times that of 0.2 m diameter column. The lateral deformation of stone column along with the depth of stone column for different diameters is shown in Figure 9. As expected, the bulging decreases with increase in diameter of stone column. For instant, as diameter increases from 0.1 to 0.3 m diameter, bulging decreases about 31%.
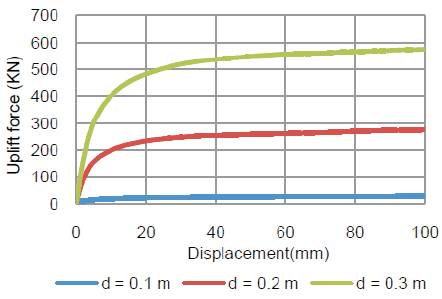
Figure 8. Uplift force Vs. Displacement for different diameter of stone column
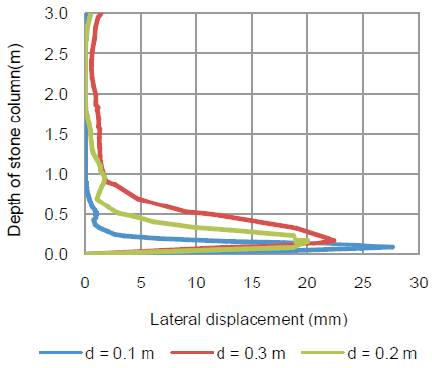
Figure 9. Effect of diameter of stone column material on lateral displacement of stone column
It is believed that as the length of column increases, the uplift resistance increases. To check this phenomenon, in this section four different length of stone column is being considered. As can be seen in Figure 10, the uplift resistance increases as the length of anchored stone column increases. For instant, as length of column increases from 1.8 m to 2.7 m; the uplift resistance increases from 32 to 55 KN, which is about 41%.
The lateral deformation developed along the depth of the anchored stone column is illustrated in Figure 11 for different length of anchored stone column. It can be seen that as length of column increases the bulging decreases. This may be due to more amount of resistance provided by surrounding soil against uplift resistance.
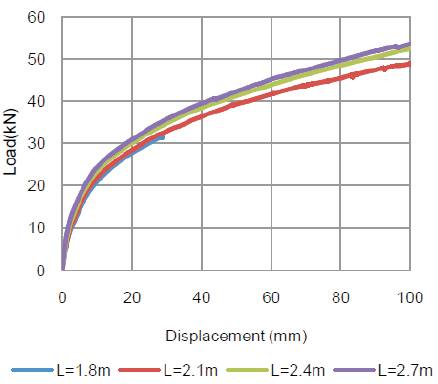
Figure 10. Uplift force Vs. Displacement for different length of stone column
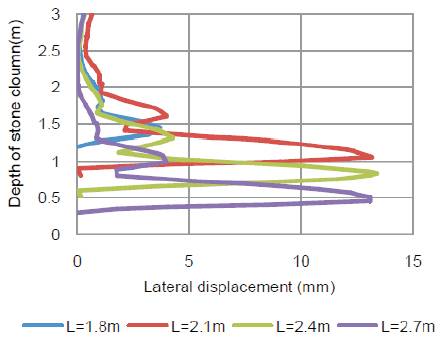
Figure 11. Effect of length of stone column material on lateral displacement of stone column
Figure 12 indicates the effect of geosynthetic on uplift force-displacement behaviour of anchored stone column for different stiffness of geosynthetic material. From this figure it can be observed that with increase in modulus of geosynthetic material, uplift resistance of stone column increases. For example, as stiffness of the geosynthetic increases from 100 to 500 kN/m, uplift resistance increases by 19%. This may be due to the higher confining pressure developed with the increase in the stiffness of geosynthetic.

Figure 12. Uplift force Vs. Displacement for different stiffness of geosynthetic
The bulging developed along the length of anchored stone column for different stiffness of geosynthetic is illustrated in Figure 13. It can be seen that with increase in depth of stone column, bulging increases and attained a maximum bulging near the bottom portion of stone column. This depth from the bottom of the stone column is 0.30 m i.e. 2 times that of the diameter of the stone column. It can also be observed that bulging of stone column decreases with increase in stiffness of geosynthetic. This may be attributed to the higher stiffness of stone column with increase in stiffness of geosynthetic.

Figure 13. Effect of length stiffness of geosynthetic on lateral displacement of stone column
Effect of stone column diameter, internal friction angle of stone column material, cohesion of soft soil, geosynthetic stiffness and stone column length on uplift force- displacement and bulging behaviour of anchored stone column were carried out by employing two -dimensional finite element modelling. Based on the present study, following conclusions are drawn.