[1]
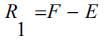
Existence of redundancy in structures plays an important role in increasing their safety and reliability. However, using state-of-the-art deterministic and probabilistic approaches, all possibilities for estimation of redundancy (e.g. due to occurrence of different damage scenarios) have not been considered. One of the methods to quantify the presence of uncertainties in a system is to use interval variables. In this work, a new method for estimating the redundancy using interval structural analysis is developed. This method, hereafter referred to as Interval Redundancy Analysis (IRA), is robust and considers possibilities of strength reduction for each element leading to failure. Independent intervals for reduction of the strength for five damage scenarios of intact, slightly damage, moderately damaged, severely damaged, and completely damaged as well as strength of each element are considered. A numerical example to show the behavior of the developed method with comparison to Monte-Carlo simulation results is presented.
Redundancy in a structural system is defined as the ability of the system to redistribute the load of the damaged members which can no longer sustain it to the other undamaged members. Similarly, redundancy in a structure is referred to the extent of damage a structure can experience without losing its functionality. Therefore, a structure is not considered redundant if the failure of one structural component causes the failure of the entire structure and loss of its functionality (Yoshihiro and Yakov 2011).
Although redundancy is usually associated with the degree of static indeterminacy, it is conceptually completely different (Frangopol and Curley 1987). Static indeterminacy pertains solely to the form of a structure in its undamaged state and an increase in the degree of static indeterminacy does not necessarily lead to increase of structural integrity (Fang and Fan 2011). In many researches performed, it has been demonstrated that the degree of static indeterminacy is not a consistent measure for structural redundancy. Therefore, structures with lower degrees of static indeterminacy have a greater level of redundancy than those with higher degrees of static indeterminacy. Generally, even using complete deterministic and probabilistic approaches, all possibilities for estimation of redundancy has not been accurately considered. This is mainly because of occurrence of different damage levels and scenarios.
One method to quantify the presence of impreciseness in a system is the interval or the unknown-but-bounded analysis. The interval representation transforms the point values in the deterministic system to inclusive set values in the system with bounded uncertainty. The interval representation of uncertainty in the parametric space has been motivated by the lack of detailed probabilistic information on possible distributions of structural parameters and/or computational issues in obtaining solutions.
In this work, a new method for determining the redundancy, using the interval structural analysis, is developed. Independent intervals for reduction of the strength for five damage scenarios of intact, slightly damage, moderately damaged, severely damaged, and completely damaged as well strength in each element are considered. Then, the bounds of the residual redundancy as well as redundancy for each member for each damage scenario are calculated. This leads to the determination of the lower-bounds of redundancy for each failure mode with consideration of uncertainties.
Structural redundancy and robustness has increasingly become a crucial issue in the last few decades following occurrence of major failures of structures due to both natural phenomena as well as man-made hazards. The concept of redundancy has first developed following the partial collapse of the Ronan Point high-rise building in London in 1968 due to relatively small gas explosion. In 1974, the Lafayette road St. Paul Bridge over the Mississippi River in Minneapolis survived despite of the failure of main girder in the central span. The next significant event in 1976 was the Ontario-35 bridge at Meiden (made of welded plate continuous over three spans) survived after the complete fracture of one girder in the lateral span of the bridge because of availability of suitable alternative load path of structure called “failed safe” structure. Silver Bridge in West Virginia is another kind of single load path structure collapsed in 1976 because of the lack of suitable alternative load path (also called “weakest link” structure). The aforementioned events emphasized the need for additional research towards the development of new concepts and methods in this field.
In last few decades the effects of prescribed damage scenario has been considered on structural systems with different specifications for buildings, bridges, and offshore platforms. Frangopol and Curley (1987) investigated analytically on the effect of damage and redundancy on reliability of truss and bridges systems based on a definition of structural redundancy to develop the theoretical concepts and illustrated their practical applications. Extensive efforts have been made in redundancy analysis, especially in a quantitative assessment (Frangopol et al. 1992) in which, a non-linear analysis is conducted to estimate redundancy of various types of frames considering heat induced by fire and loss of columns. Ghosn and Frangopol (2007) presented a retrospective on the quantification of the system redundancy during the structural design and safety assessment of structural systems.
Biondini and Frangopol (2008) showed the effects of prescribed damage scenario as a progressive deterioration of the material properties on robustness of structural systems with different degrees of static indeterminacy. Wada et al. (2008), in a study for the Japan Iron and Steel Federation, discussed the resistance of the steel frames against heat induced by fire and loss of columns by accident (e.g. explosion and impact of a crash). Fang and Fan (2011) presented the essentials of redundancy as well as its significance within the wider context of structural safety. Their work discussed different levels of structural safety (i.e. reliability and robustness) from a broader perspective, in which reliability refers to the pristine or intact state of structure, whereas robustness corresponds to local damage states, concluding that the existence of redundancy assists in: (1) enhancing the safety margin of a structure in its intact state; and (2) mitigating the sensitivity of the structure to localized damage under an accidental situation (Fang and Li 2009).
There are several definitions of structural redundancy in conjunction with damage assessment based on deterministic, probabilistic, and fuzzy interpretations of several alternative measures (Furuta et al. 1985). These definitions include:
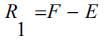
where, F is the number of unknown reactive forces and E is the number of independent equilibrium equations
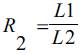
Where, L1 = load carrying capacity (collapse load) of the intact (undamaged) structure and L2= Design load
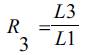
Where, L3= load carrying capacity (collapse load) of the damage structure.
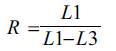
Also:
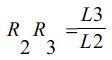
R2R3 indicates whether the damaged structures will survive the design load.
As explained earlier, the degree of redundancy, R1, does not constitute an adequate measure of the overall system strength. The redundant factors R2, R3, and R4 clearly are more suitable measures of the overall system strength for both intact and damaged structures. Structural redundancy depends on several factors including structural topology, member sizes, material properties, applied loads and load sequence (Frangopol and Curley 1987).
The interval approach to the uncertain problems is to quantify the parameters as interval variables. Interval analysis provides a powerful set of tools with direct applicability to important problems in scientific computing. Moore (1966) introduced interval analysis, interval vectors and interval matrices as a set of techniques that provides error analyses for computational results.
A real interval is a closed set defined by extreme values as:
One interpretation of an interval number is a random variable whose probability density function is unknown but non-zero only in the range of interval. Another interpretation of an interval number includes intervals of confidence for e cuts of fuzzy sets. This interval representation transforms the point values in the deterministic system to inclusive set values in the system with bounded uncertainty.
Interval arithmetic is a computational tool that can be used to represent uncertainty. In this work, the symbol (~) represents an interval quantity. Considering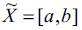
and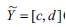 
as two interval numbers, the basic interval arithmetic operations are as follows.
Addition:
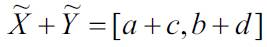
Subtraction:
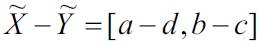
Multiplication:
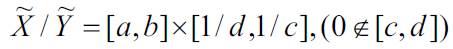
Division:
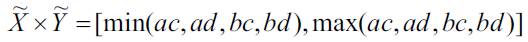
The developed method for determining the redundancy using interval uncertainty, analysis named as Interval Redundancy Analysis (ISA), is composed of the following steps:
) for one or multiple element(s) with consideration of uncertain strength as well as different uncertain damage scenarios.
) for one or multiple element(s) with consideration of uncertain strength as well as different uncertain damage scenarios.The numerical example solves the problem cited in the paper by Frangopol and Curley (1987) using the developed method. The problem is a 2D truss with 10 elements, 6 nodes and 8 active degrees of freedom (Figure 1). The cross section areas of members are A=2in2 and the modulus of elasticity is E=29000 ksi. Two concentrated loads, W, are applied to the truss. The material behavior for all members is assumed to be brittle.
Figure 1. 2D Truss Structure
The strength capacity of each member is Fy=36 ksi or Py 72 kips The strength for different damage scenarios are:
Solution: The deterministic problem is solved for residual redundancy for different damage scenarios in the case of damage imposed on one member. The results are shown in Table 1.
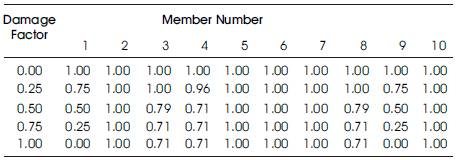
Table 1. Residual redundant factors for different damage conditions imposed on one member
The independent interval for strength capacity of each member are given as
The interval strength for different damage scenarios are:
Solution: The deterministic problem is solved for the lower bounds of interval residual redundancy and for different damage scenarios in the case of damage imposed on one member and the results are summarized and shown in Table 2.
Also, the results for the interval problem were compared and shown to be the upper bounds of the solution of a 104 Monte-Carlo simulation solution using uniformly distributed random variables.
The results for residual redundant factors as well as redundant factors obtained for different damage cases for both deterministic and interval problems are summarized in Table 3. The comparison of results obtained by two methods shows a monotonic decrease in values of both residual redundancy and redundancy factors in all failure modes. This implies that in the presence of uncertainty in the structure's strength as well as damage scenarios, the load carrying capacity of the structure significantly decreases.
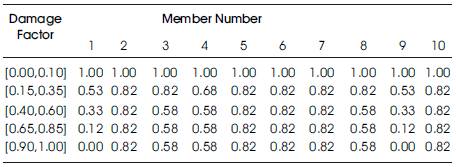
Table 2. Lower bonds of interval residual redundant for different damage condition imposed on one member
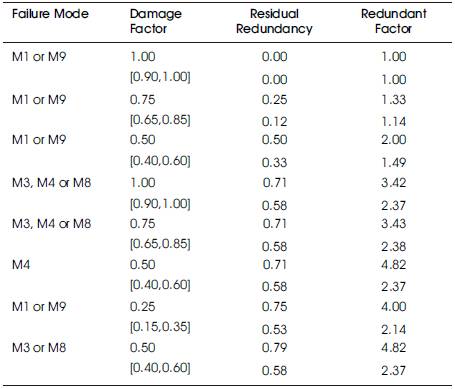
Table 3. Residual redundant factors and redundant factors for different members' damage levels for deterministic and interval (lower bounds) approaches
A new method for estimating the redundancy using interval structural analysis is developed. Independent intervals for reduction of the strength for five damage scenarios as well as possibilities of strength reduction for each element leading to failures are considered.
The results obtained by this computationally efficient method shows that in the presence of uncertainty in the structure's strength as well as damage scenarios, the load carrying capacity of the structure significantly decreases. This has not been considered in current deterministic analysis for structural redundancy. The simplicity of the proposed method makes it attractive to introduce interval uncertainty in analysis of redundancy in structures.