Subspace Clustering on High Dimensional Data
M. Bhargav * P. Venkateswarlu Reddy **
* PG Scholar, Department of Computer Science and Engineering, Sree Vidyanikethan Engineering College, Tirupati, India.
** Assistant Professor, Department of Computer Science and Engineering, Sree Vidyanikethan Engineering College, Tirupati, India.
Abstract
Due to the increase of large amount of real world, it is a difficult task for the organizations, companies, etc., to extract relevant data from large amounts of necessary and unnecessary data. Many researches will be going on from the few decades onwards. In datamining there is a concept called clustering which will be used for the smaller datasets, where it effectively makes relevant data into clusters. But the problem will arise on the larger datasets, where it will face a complexity for grouping relevant data into cluster. In this paper, analysis have been referred from many of the algorithms like subscale algorithm for finding the dense region from the dataset and DBscan algorithm for making a cluster as a result it takes dataset as an input and scans a complete dataset. The problem occurs on the time complexity and performance and also, it will follow a sequential flow of database scan. So, it takes time for relevant data values as a cluster in final result. In this analysis, it will allow the complete dataset scans at a time, processing data in parallel manner. So, the resultant data is in effective manner in a lesser time. For the improvement of previous algorithm a Map Red based DBscan for reducing time complexity and performance improvement has been used.
Keywords :
- Big Data Mining,
- High Dimensional Data,
- Subspace Clustering,
- Scalable Data Mining.
Introduction
In a few decades, the recent work will be going on a gradual increase of the data in many areas such as industry, hospitals, shopping malls, etc. The real world scenario is to obtain information from large amount dataset repositories in an effective manner. Various processing steps have been followed for obtaining the required information. The compression of gigabits of data to Megabits of data in efficient manner without loss of the original data is complex and typical task for data mining. The intention behind every information is to reduce redundancy and irrelevant data from large dataset. Each and every clustering approach will mainly focus on these elements like simplification of original data and evaluating the pattern present in the dataset. Clustering can be used in different areas like data mining, information retrieval, marketing, medical diagnostic, etc. Clustering will be able to apply on the type of attribute which are used for the data representation, complexity which will mainly occur during processing the complete data. The traditional clustering algorithms are DBscan, Hierarchical, Partitioning, Probabilistic, and Constrainbased Clustering. In general, every cluster will follow a dissimilarity measures it will have done without knowing the previous knowledge on the clustering. The distance measure will be used for finding the density or similarity of data points present in the dataset. Traditional algorithm will effectively work in a full dimensional space based on the proximity distance between the neighbour points present in the dataset. But when proximity distance between the neighbour points is increased then it does not be effectively work. Because it will make irrelevant data cluster due to the increase in dimensionality of data.
These traditional clustering algorithms will not work in an effective and efficient manners for the high dimensional data. The curse of dimensionality will mainly occur on the high dimensional data i.e., a) when the dimensionality of the data increases the relation between the similar and dissimilar data points becomes less. b) Different dimensions of the data will be grouped based on the similar dimensional data point present in a same dimension. To overcome the redundancy of data points, irrelevant data points here use a subspace clustering. It will make a cluster based on the subspaces present in a full dimensional space. In this analysis, are found clusters in all possible subspaces of dataset. In general, kdimensional data has 2k−1 possible axis-parallel subspaces.
1. Literature Review
Clustering is a grouping of a similar data point into a cluster. This cluster will be classified easily in lower dimensional data. But it is facing difficulty for the higher dimensional data present in database. In general, clustering will follow the traditional algorithms like fuzzy clustering, clustering high dimensional data, subspace clustering, and clustering with constraints. For many years, the researchers were concentrating on the improvement of clustering not only in full dimensional space, but also in subspace present in full dimensional space. In the following, many researches have explained their problem for finding the accurate solutions for the problem.
1.1 Fuzzy Cluster
Rongu Li and Guoxia Li was described about the fuzzy cluster analysis results. Cluster analysis is a similar object which belongs to the same similarity between the neighbour objects grouped. There are large number of clustering methods which has been used to examine the multidimensional data by identifying a cluster from homogeneous data. In general, the fuzzy logic values lie between 0 and 1 and in similar ways the fuzzy clustering will identify the membership function for finding the cluster based probability of every cluster present in the dataset.
Fuzzy cluster will use the mathematical model and formulas for finding the cluster value. In NAA, data for the 32 elements on the 86 samples were discovered by fuzzy cluster analysis. For these examples each and every sample of the cluster belongs to the complete set of clusters present in all samples of the data. NAA technologies very useful for measuring the tens of elements from given samples of data. Fuzzy clustering will be used to increase the comprehensive results, and also gives clear objective for the problem statement.
1.1.1 Advantages and Disadvantages
- Fuzzy clustering can be used for the segmentation of the market.
- It can be used to modify the segmentation techniques with the help of generating a fuzzy score for each customer.
- It will provide a more precise measure for the company delivery values to the customers and for the profitability of the company.
- It will have the capability to express ambiguity for assigning objects into a cluster.
- It produces a spherical cluster and it will support a cluster to change its dependent shape for the data.
1.2 Clustering High Dimensional Data
Singh Vijiendra and Sahoo Laxman analyzed that the clustering problem will be identified on the homogeneous groups of data, finding cluster values based on similarity measures. In general, the clustering consisting of the data values present in a cluster will have the same kind of relationship between the neighbour data values present in the same cluster. In density-based cluster definition, that takes under consideration of attribute similarity in subspaces in addition as a neighborhood graph density and allows us to observe clusters of discretionary form and size. A novel biclustering algorithmic program that exploits the Zero-suppressed Binary Decision Diagrams (ZBDDs) data structure to address the process challenges. This technique will realize all biclusters that satisfy specific input conditions, and it is scalable to sensible organic phenomenon knowledge [5]. Moreover, we have a tendency to avoid redundancy within the result by choosing solely the foremost attention-grabbing nonredundant clusters. They introduced the bunch algorithmic program DB-CSC, that uses a set purpose iteration technique to expeditiously determine the bunch answer. They have a tendency to prove the correctness and quality of this mounted purpose iteration analytically [2]. But it will have varying data values present in the different clusters. Most of the traditional clustering algorithms will effectively work on the low dimensional datasets. But it faces a problem in handling the high dimensional dataset due to the decrease of similarity between the data values present in the same cluster will be increased. The researchers provide a brief introduction to cluster analysis, and so specialise in the challenge of agglomeration high dimensional information. We tend to gift a quick summary of many recent techniques, as well as a lot of elaborated description of recent works that uses a concept-based agglomeration approach [8].
Cluster algorithms are surveyed for knowledge sets showing in statistics, engineering, and machine learning, and illustrate their applications in some benchmark knowledge sets, the salesman problem, and bioinformatics, a brand new field attracting intensive efforts. Many tightly connected topics, proximity live, and cluster validation, are mentioned [6]. To increase the similarity of data values within the cluster, will be done only by removing the irrelevant data values present in the dataset. Suppose if the number of irrelevant data values is reducing automatically, the performance of the relevant data values present in the cluster will be increased [9] .
Clustering methods will mainly depend on either distance or densities. It is a difficult task to identify the relevant clusters in the high dimensional dataspace. The ideas of microarray technology and the basic parts of cluster on organic phenomenon information were discussed. They tend to divide cluster analysis for organic phenomenon information into 3 classes. Then gift specific challenges were tend to be pertinent to each cluster class and introduce many representative approaches. Also, conjointly discuss the problem of cluster validation in 3 aspects and review numerous ways to assess the standard and dependableness of cluster results. So, it will categorize into different subspaces present within the cluster then only it will have obtained perfect data values [7]. For these problems, the author has used a Multiobjective Subspace Clustering algorithm for forming efficient clusters at the final result. It first discovers the subspaces present in the dense regions of a dataset and then it will produce a subspace clusters.
1.2.1 Advantages and Disadvantages
- It performs a subspace relevance analysis based on finding a dense region and sparse region with their respective locations in the dataset.
- To extract necessary information from typical expression data, it will consists of a high level of noise data.
- Different subspace cardinalities vary based on the unit densities such as finding dense units in all subspaces of dataset by utilizing an absolute unit density of a threshold value.
1.3 Subspace Clustering
Rene Vidal was discussed on clustering problem in past few years. The availability of data will be obtained from modalities and sources. Suppose millions of cameras were arranged on the buildings, airports, streets and cities around the world, it will be assumed as a complex task for acquiring the data, processing the data, storing the data and also execute these tasks in parallel [3].
In Sparse Subspace Clustering cluster knowledge points are a union of low-dimensional subspaces. Paste your text here and click on "Next" to observe this text redactor does it's issue. Don't have any text to check "Select Samples" presents a survey of the assorted mathematical space clump algorithms alongside a hierarchy organizing the algorithms by their shaping characteristics. They tend to then compare the two main approaches of mathematical space clustering victimization empirical measurability and accuracy tests and discuss some potential applications wherever subspace clump might be notably helpful and the key plan is that, among infinitely several potential representations of a knowledge purpose in terms of different points, a distributed illustration corresponds to choosing a number of points from identical topological space [1]. The SSC algorithm are often resolved expeditiously and might handle knowledge points close to the intersections of subspaces. Another key advantage of the projected algorithmic rule with relevancy has the state of the art that will deal with knowledge nuisances, like noise, thin far entries, and missing entries, directly by incorporating the model of the information into the thin improvement program. A review of such progress, has been presented including a variety of existing topological space agglomeration algorithms together with associate degree experimental analysis on the motion segmentation and face agglomeration issues in PC vision. They also attempt to clarify:
(i) The various downside definitions associated with mathematical space clump in general.
(ii) The particular difficulties encountered during this field of research.
(iii) The varied assumptions, heuristics, and intuitions forming the premise of various approaches and
(iv) However many outstanding solutions tackle totally different issues [4], the main intention of these subspace clustering is to arrange high dimensional dataset values within a low dimensional dataset region without any loss of data [8].
Example is that computer vision reducing the high pixel image into low pixel image without changing original data points. From few decades onwards many researchers were finding on the significant progress in the high dimensional data is speeded into linear and affine subspaces and this will mainly concentrate to reduce noise, data with missing values, outlier's data values, unknown number of dimensions, unknown number of subspaces, etc. For this, the problem can be solved by using GPCA algorithm, and it will be able to handle the unknown subspaces and unknown dimensions of dataset values.
1.3.1 Advantages and Disadvantages
- Finding the number of dimensions in a subspace and also outliers and noise data values present in a dataset.
- It assumes that the number of dimensions and their subspaces are known.
- Sometimes, cluster formation in multiple levels will be also be meaningless.
1.4 Clustering with Constraints
Bi-Ru Dai, et al. was interested to implement their application dependent parameters or domain knowledge on the datamining systems. In this analysis, constrains are modelled when attributes are employed. The constrained based clustering will be done with the help of satisfying the constraints for the given attributes of dataset. In general dataset attributes, can be classified in to two types: 1) Numerical attributes and 2) Categorical attributes.Numerical attributes consist of an ordered value, such as weight of a person and speed of moving person. Categorical Attributes consist of unordered values, such as blood type of an animal and the brand of cycle. For example, weather forecasting mainly depends on time and temperature attributes, and based on that particular values it indicates the atmosphere changes in earth. The problem arises in these analysis is boundary specified for a value lies between the particular region then if a same values present in the other boundary it may collide. The author introduced a progressive constraint relaxation technique to improve the complete performance of clustering results and to handle the dependency among the attribute values of dataset. The partition based algorithm, CDC is performed well for the cost of clustering result, but it will take more time for data values to traverse between cluster to obtain a satisfactory result by spending minimum cost.
1.4.1 Advantages and Disadvantages
- It is used for the validation of an empirical knowledge in CDC and performs well in the cost of clustering results.
- It will be used to handle the constrained clustering problem for dataset.
- It will take more time for data points to traverse between the clusters for achieving a satisfactory result.
2. Proposed Work
The main goal for these analysis is to make relevant cluster from dataset which consists of both relevant and irrelevant data and to reduce the time complexity and increase the performance. The proposed work will have performed effectively on clustering with the help of Hadoop platform. It will create multiple threads and executes the process in parallel and then it will automatically reduce a time complexity and also increases performance. The MapReduce concept will be used to processing the threads and get effective results finally. In general, to execute MapReduce program, it requires a mapper, reducer and main class in Hadoop platform by using parallel DBSCAN algorithm.
Datamining has two major clustering algorithms like kmeans and DBSCAN. But k-means algorithm mainly works on prototype, and it will find an approximate class for a given dataset values. When compared to k-means algorithm, the DBSCAN will be efficient to find the free class and identify the noise points present in the dataset without knowing the number of classes to be formed in advance. In parallel DBSCAN algorithm, the dataset D consists of data objects for all unmarked objects in dataset, an object P, and then marked P as a visited object. Determining the core object by checking on the region query for an object P, suppose P is not a core object then mark P as a noise object and reselect another unmarked object from dataset. If P is a core object, create a new class C for an object P and iterate for remaining objects within the P object to seed an object to make region query for expanding class C. Until no new objects in dataset is not interested to join in the class C, DBSCAN depends on the e (radius) and MinPts (density threshold) parameters. When the given objects lie within the radius and not less than the density threshold value then make it in to cluster.
DBSCAN algorithm will defined in the following terms:
- The P object is said to be ε region of P, when it is present within the area having ε (radius).
- The P object is said to be core object, when the given objects present in ε (radius) and not less than the MinPts (density threshold).
- The Q object is said to be directly density reachable, when Q object contains P object by checking the condition within the ε region of Q object.
- Suppose dataset D consists of n objects, i.e., {P_1,P_2,…,P_n}, P_1=Q, P_n=P, for P_i ε D (1 ≤ i ≤ n), P_i is density reachable on ε (radius) and MinPts (density threshold), if P_(i+1) is starting.
- P is starting from Q is said to be density reachable with ε (radius) and MinPts (density threshold).
- If the P object is starting from O object, it is said to be density reachable on ε (radius) and MinPts (density threshold) and Q object is starting from O object is also density reachable, then P object to Q object is said to be density-linked.
- If P object is said to be noise object only when it does not belong to any class.
Algorithm 1: Finding Dense Items in Dataset
Input: j dimension, set K contains n large integers and unique random values.
1. Arrange P1 , P2 ,…,Pn , show that 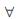 Px ,Py ,ε Database, Pix ^j ≤ Piy
Px ,Py ,ε Database, Pix ^j ≤ Piy
2. for a=1 to n-1 do
3. coreset ← map (P1 )
4. nNeighbours ← 1
5. nextvalue ←i+1
6. while nextvalue ≤ n and Pinextvalue ^ j- Pi1 < ε do
7. Adding map (Pnext ) to coreset
8. increment nNeighbours
9. increment nextvalue
10. end while
11. if nNeighbours > τ then
12. finding all sets of dense items, u from the core-set values ((|coreset|)/(τ+1))
13. end if
14. for 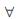 dense items u finds in the existing step do
dense items u finds in the existing step do
15. Adding entries {sum(u),u}to DI
// DI is used to store dense items
16. end for
17. end for
18. return DI
// each entry in Di is a pair of having sum and u values.
Algorithm 2: Finding Maximal Subspace Clusters in Dataset
Input: Database should have m× k values; set k having m random, large integers and unique
1. Hashtable Table ←{}
//An entry h_x having {sum,u,s}.
2. for L=1 to k do
3. DI← denseitems (j)
// get candidate dense items in j dimensions
4. for 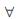 DI= {sum,u} ε DI do
DI= {sum,u} ε DI do
5. if any key of hashtable h Table.h_x= =sum then
6. Adding j dimension to subspace h_x.S
7. else
8. Adding new entries {sum, u, L}to h Table
9. end if
10. end for
11. end for
12. for 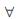 set of entries {hx ,hy ,…} ε h Table do
set of entries {hx ,hy ,…} ε h Table do
13. if hx .S=hy .S=⋯ then
14. Adding entries {S, hx .u∪hy .u∪…} to form clusters
// The formed clusters having maximal dense items in the relevant subspaces
15. end if
16. end for
17. make run of DBSCAN on each entries of formed clusters
18. return formed clusters
In DBSCAN algorithm, when an object belongs to 2 different classes, then that object belongs to one class and there is no relationship between the 2 classes. For the improvement of DBSCAN algorithm merging 2 classes into a new class will be done, and also parallelizing for the determination of core object. In this analysis, a new concept has been introduced called sharing object.
2.1 Sharing Object
Figure 1 explains about the sharing object, i.e., the core objects P and Q belongs to different classes. If an O object starting from P object, Q object are density reachable, then O object is called sharing object. If O object is a core object then O object is called sharing core object, and also if sharing core object is existing in different classes, then these classes can be merged into a new class.
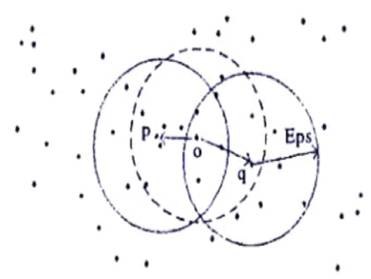
Figure 1. Overlapping of Clustering Objects in a Region
Parallel DBSCAN algorithm for clustering using map reduce technique will be divided into 4 stages as shown in Figure 2.
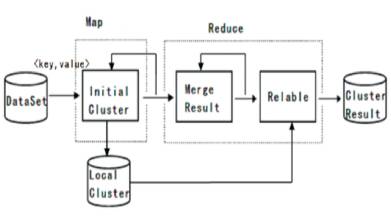
Figure 2. Data Processing Stages in Parallel DBSCAN
2.1.1 First Stage
The input dataset will cut into small parts having equal size.
2.1.2 Second Stage
These parts are split into nodes in a cluster, then only all the nodes in a cluster will run mapping function by themselves in parallel for calculating and processing that parts.
- Initial Clustering: It is done for any unlabeled P object in the dataset identifying the number of objects in its region for determining a core object. If P is a core object which consists of the remaining objects within the region having an initial class C, and marked that objects within the same (cluster identifier) Cid. Suppose if P object and the objects presents in the Q object consists of same Cid (cluster identifier). Repeat this process until all the objects in the dataset are identified. The end of this process will get an initial clusters and noise objects.
- Merging Result: Sharing core object will be found here, then merging the 2 classes. If no object exist in the different classes, then merging initialize class has been completed.
2.1.3 Third Stage
Merging the result of each processor.
2.1.4 Fourth Stage
The output comes with clustering results.
Algorithm 3: DBSCAN-Map (partition p)
Input: p: a partition, Varp= read input data;
1. kd=buildspatialindex(p);
// building the KDTree spatial index
2. kd.DBSCANCluster(p);
// running DBSCAN on p with the KD Tree index
3. for each point Pts in p do
4. If Pts.is boundary do
// storing the result of boundary points to HDFS
5. Output (Pts.index, partition.index + Pts.cid+ Pts.iscore);
6. end if
7. else // storing result of other points to local disk
8. writeLocal(Pts.index, partition.index + Pts.cid);
9. end else
10. end for
Algorithm 4: DBSCAN-Reduce (key, values)
Input: key 1, value 1; map output pair {pointindex, partition.index+Pts.cid+Pts.isCore}
Var cidlist= null; // set to store cluster IDs for the same index point Var merge = false;
1. for each point Pts in values do
// values are a set of CID for the same indexes of points
2. if Pts.iscore do // if point Pts is a core point
3. mergeitems = true;
4. end if
5. if !cidlist.contains(Pts.cid) and Pts.cid!= noise do
6. Pts.cid and cidlist are combined into cidlist
7. end for
8. end for
9. If mergeitems == true do // storing the result to HDFS
10. Output (key, cidlist+ true) // key is point index
11. end if
12. else
13. Output (key, cidlist+ false)
14. end else
Algorithm 5: Merge Boundary Result (key 1, value 1)
Input: DBSCAN-Reduce
Output: MM // MM is merge list,
VarM = null; // set to store cluster IDs of merged clusters
1. data=Hdfs.open (DBSCANReduce output);
2. for each point Pts in data do
3. if Pts.iscore do
4. Finding out all merge combination of Pts and put them into merge list set MM
5. end if
6. Finding the same combination from MM
7. end for
8. repeat
9. for each CCC1, CC2 ∈MM do // CC1 and CC2 are merge combinations
10. if CC1∩CC2! = Ø then combining CC1 and CC2
11. end for
12. until all merge combinations in MM do not change anymore
13. for each CC ∈ MM do // For example, {cc1, cc4, cc3} is sorted as {cc1, cc3, cc4}
14. Sorting CC in the rise order by CID
15. end for
16. return MM
The mapper reducer and main class will be divided their complete work into three parts, then it will handle the complete process in an easier manner. The complete map reduce process will be explained in detail with the help of the algorithm.
3. Experimental Results
For processing the dataset in the single system, first make all respective configuration for doing clustering work. Hadoop is a platform to create multiple threads and it is used for parallel processing of the data, the processed data will be clustered at a final stage. For effective clustering of dataset, a parallel DBSCAN algorithm has been applied. Madeleon dataset will be used for clustering process and also time complexity is compared on both Hadoop platform and normal CPU based system. Figure 3 gives a comparison of these two varied systems. Here taking input as a madeleon dataset and processing will be on intel core i5, Linux operating system, hard disk having 35GB, 4GB RAM, Hadoop platform. The final clusters that will be obtained in Parallel DBSCAN is 8.2 seconds, but in Normal DBSCAN gets clustered in 172.3 seconds. Hence here has been achieved successfully improvement by using Parallel DBSCAN algorithm.
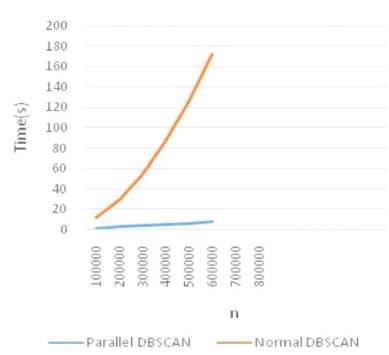
Figure 3. Comparison Graph for Normal DBSCAN and Parallel DBSCAN
Conclusion
These analysis deals with the reduction of time complexity and scalability of clusters on large datasets. Traditional clustering algorithms will effectively work on lower dimensional datasets. But it will not effectively work on higher dimensional datasets. For the improvement of clustering algorithm, parallel DBSCAN based algorithm was introduced, which will process large datasets in parallel and it automatically reduces the time complexity and scalability when compared to traditional clustering algorithms. The parallel DBSCAN algorithm will be developed based on the existing DBSCAN algorithm.
References
[1]. Elhamifar E., and Vidal R., (2013). “Sparse subspace clustering: Algorithm, theory, and applications”. IEEE Trans. Pattern Anal Mach Intell., Vol. 35, No. 11, pp. 2765- 2781.
[2]. Günnemann S., Boden B., and Seidl T., (2012). “Finding density-based subspace clusters in graphs with feature vectors”. In: Data Mining and Knowledge Discovery, Springer, US, Vol. 25. pp. 243-269.
[3]. Vidal R., (2011). “Subspace clustering”. IEEE Signal Proc Mag, Vol. 28, No. 2, pp. 52–68.
[4]. Kriegel HP., Kröger P., Zimek A., and Oger PKR, (2009). “Clustering high-dimensional data: A survey on subspace clustering, pattern based clustering, and correlation clustering”. ACM Trans Knowl Discov Data, Vol. 3, No. 1, pp. 1–58.
[5]. Yoon S., Nardini C., Benini L., and De Michelin G., (2005). “Discovering coherent biclusters from gene expression data using zero-suppressed binary decision diagrams”. IEEE/ACM Trans Comput BiolBioinforma, Vol. 2, No. 4, pp. 33.
[6]. Xu R., and Wunsch D., (2005). “Survey of clustering algorithms”. Neural Netw IEEE Trans., Vol. 16, No. 3, pp. 645-678.
[7]. Jiang D., Tang C., and Zhang A., (2004). “Cluster analysis for gene expression data: A survey”. IEEE Trans Knowl Data Eng, Vol. 16, No. 11, pp. 1370–1386.
[8]. Parsons L., Haque E., and Liu H., (2004). “Subspace clustering for highdimensional data: A review”. ACM SIGKDD Explor Newspp, Vol. 6, No. 1, pp. 9105.
[9]. Steinbach M., Ertoz L., and Kumar V., (2004). “The challenges of clustering high dimensional data”. In: New Directions in Statistical Physics, Springer, Berlin Heidelberg, pp.273–309.
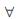 Px ,Py ,ε Database, Pix ^j ≤ Piy
Px ,Py ,ε Database, Pix ^j ≤ Piy dense items u finds in the existing step do
dense items u finds in the existing step do

